Konstruierbares Polygon

In der Mathematik ist ein konstruierbares Polygon ein regelmäßiges Polygon, das mit Zirkel und (unmarkiertem) Lineal – den Euklidischen Werkzeugen – konstruiert werden kann. Zum Beispiel ist das regelmäßige Fünfeck konstruierbar, das regelmäßige Siebeneck hingegen nicht.
Konstruierbarkeit

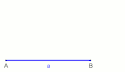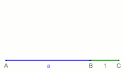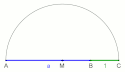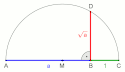
Durch die Ergänzung der konstruierten Zahl mit = 1 ist mittels Thaleskreis konstruierbar.
Zahlenbeispiel:
Um den Begriff „mit Zirkel und Lineal konstruierbar“ mathematisch präzise zu erfassen, muss definiert werden, was mit diesen Werkzeugen möglich ist. Wir gehen davon aus, dass am Anfang einer jeden Konstruktion zwei Punkte gegeben sind. Mit dem Lineal kann man dann eine Gerade durch zwei Punkte konstruieren, mit dem Zirkel einen Kreis durch einen Punkt um einen anderen Punkt als Mittelpunkt. Außerdem seien die Schnittpunkte von Geraden und Kreisen konstruierbar.
Aus diesen Grundkonstruktionen lassen sich eine Reihe weiterer Konstruktionen ableiten, wie die Konstruktion einer Mittelsenkrechte oder das Fällen eines Lotes. Man nennt dann eine positive reelle Zahl konstruierbar, wenn man zwei Punkte konstruieren kann, sodass der euklidische Abstand zwischen ihnen gleich dem Betrag dieser Zahl ist (wobei der Abstand zweier vorgegebener Punkte als 1 definiert wird). Ist beispielsweise die Zahl konstruierbar, so kann man mit Hilfe des Höhensatzes zwei Punkte mit Abstand konstruieren. Sind zwei Zahlen und konstruierbar, so mit Hilfe des Strahlensatzes auch deren Produkt und der Kehrwert , sowie durch Abgreifen eines Abstandes deren Summe und Differenz .→ Siehe zu den algebraische Operationen auch den Artikel Konstruktion mit Zirkel und Lineal. Ein Winkel heiße konstruierbar, wenn die Zahl konstruierbar ist; der Sinn dieser Definition erschließt sich schnell durch Betrachten des Einheitskreises.
Um nun ein regelmäßiges -Eck zu konstruieren, genügt es, den Zentriwinkel zu konstruieren, denn wenn man den Mittelpunkt des -Ecks und eine Ecke gegeben hat, lässt sich ausgehend von der Verbindungsgeraden durch Mittelpunkt und Eckpunkt der nächste Eckpunkt konstruieren. Ist umgekehrt ein regelmäßiges -Eck gegeben, so kann man den Zentriwinkel abgreifen. Zur Beantwortung der Frage, ob das -Eck konstruierbar ist, ist man also auf den Fall zurückgeführt, zu entscheiden, ob der Zentriwinkel konstruierbar ist.
Konstruierbarkeit von Zahlen
Eine Zahl heißt genau dann mit Zirkel und Lineal konstruierbar, wenn sie z. B. eine ganze Zahl, eine Dezimalzahl mit endlicher Anzahl Nachkommastellen oder die positive Wurzel aus einer dieser Zahlen (siehe Anwendungsbeispiel Höhensatz) ist, genauer gesagt die Länge einer Strecke ist, die wie hier beschrieben konstruiert werden kann.
In der synthetischen Geometrie werden auch Punkte und Zahlen untersucht, die etwas allgemeiner aus einer (fast) beliebigen Vorgabemenge von Streckenlängen konstruiert werden können. Dazu werden Körpererweiterungen der rationalen Zahlen betrachtet, die euklidische Körper und damit Koordinatenkörper einer euklidischen Ebene (im Sinne der synthetischen Geometrie) sind. Die Konstruierbarkeit mit Zirkel und Lineal einer Zahl bedeutet dann, dass sie eine Koordinate eines aus den Vorgaben konstruierbaren Punktes in der Ebene ist. → Siehe zu diesen Begriffsbildungen auch den Artikel euklidischer Körper!
Kriterium für Konstruierbarkeit
Carl Friedrich Gauß zeigte 1796, dass das regelmäßige Siebzehneck konstruierbar ist. Dazu wies er nach, dass die Zahl als Ausdruck dargestellt werden kann, der nur ganze Zahlen, arithmetische Grundoperationen und verschachtelte Quadratwurzeln enthält. Durch die in seinen Disquisitiones Arithmeticae entwickelte Theorie gelang es Gauß fünf Jahre später, eine hinreichende Bedingung für die Konstruktion regelmäßiger Polygone anzugeben:
- Wenn das Produkt einer Potenz von 2 mit paarweise voneinander verschiedenen Fermatschen Primzahlen ist, dann ist das regelmäßige -Eck konstruierbar.[1]
Gauß wusste zwar, dass die Bedingung auch notwendig ist, hat allerdings seinen Beweis hierfür nicht veröffentlicht. Pierre-Laurent Wantzel holte dies 1837 nach, weshalb das Resultat auch als Satz von Gauß-Wantzel bekannt ist.[2]
Man kann zeigen, dass eine Zahl genau dann das Produkt einer Potenz von 2 mit verschiedenen Fermatschen Primzahlen ist, wenn eine Potenz von 2 ist. Hierbei bezeichnet die Eulersche φ-Funktion.
Zusammenfassend: Für eine Zahl sind die folgenden Aussagen äquivalent:
- Das regelmäßige -Eck ist mit Zirkel und Lineal konstruierbar.
- mit und paarweise verschiedenen Fermatschen Primzahlen .
- Dabei steht das für m=0 sich ergebende leere Produkt definitionsgemäß für die Zahl 1.
- für ein .
Sind insbesondere und teilerfremd und sowohl das -Eck als auch das -Eck konstruierbar, so ist wegen auch das -Eck konstruierbar. Für diese Tatsache lässt sich auch direkt die geometrische Konstruktion angeben, denn wenn und teilerfremd sind, so gibt es nach dem Lemma von Bézout zwei ganze Zahlen und mit Indem man nun -mal den Zentriwinkel des -Ecks und -mal den Zentriwinkel des -Ecks anlegt, hat man den Winkel – und damit auch das -Eck – konstruiert.
Konkrete Konsequenzen des Kriteriums
Trotz intensiver Suche wurden über die fünf bereits Gauß bekannten Fermatschen Primzahlen 3, 5, 17, 257 und 65537 hinaus bis heute keine weiteren gefunden. Es besteht sogar die plausible Vermutung, dass es keine weiteren Fermatschen Primzahlen gibt.
Sollte es tatsächlich nur fünf Fermatsche Primzahlen (FP) geben, dann sind unter den Polygonen mit ungerader (!) Eckenzahl genau die folgenden 31 theoretisch konstruierbar:[3]
|
|
|
|
Alle anderen konstruierbaren Polygone (dann mit gerader Eckenzahl) sind das Quadrat oder sie ergeben sich durch (fortgesetztes) Verdoppeln der Eckenzahl.
Für das Dreieck, Fünfeck, Siebzehneck, 257-Eck und selbst für das 65537-Eck sind Konstruktionsanweisungen bekannt. Damit liegen nur für diese ungeraden Polygone Konstruktionsanweisungen vor. Im November 1879 begann Johann Gustav Hermes sein Werk zum 65537-Eck. Mehr als zehn Jahren danach übergab er an das Mathematische Institut der Universität Göttingen einen Koffer[4] mit einem Manuskript. Darin beschrieb und bewies er die theoretisch mögliche Konstruktion des 65537-Ecks allein mit Zirkel und Lineal.[5]
Lässt man zur Konstruktion zusätzlich ein Hilfsmittel zur Dreiteilung eines Winkels (Trisektion) zu, so sind alle regelmäßigen Polygone mit Eckenzahlen der Form konstruierbar, wobei mit verschiedene Pierpont-Primzahlen größer als drei der Form sind. Auf diese Weise sind beispielsweise auch das Siebeneck[6], das Neuneck und das Dreizehneck konstruierbar.
Werden als zusätzliche Hilfsmittel z. B. die Quadratrix des Hippias, die archimedische Spirale oder die Sinuskurve akzeptiert, die neben der Dreiteilung auch Teilungen mit gleich große Winkel ermöglichen, wie das Beispiel Neunzehneck zeigt, sind theoretisch sämtliche regelmäßige Polygone konstruierbar.
Daraus folgt: Lässt man als zusätzliches Hilfsmittel nur die Dreiteilung eines Winkels (Trisektion) zu, ergibt sich für regelmäßige Polygone bis zum 1000-Eck folgende Tabelle für die Konstruktion mit Zirkel und Lineal (J), bzw. zusätzlich Trisektion (T) oder nicht (N):
| Eckenzahl | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Konstruierbar | J | J | J | J | T | J | T | J | N | J | T | T | J | J | J | T | T | J | T | N | N | J | N | ||
| Eckenzahl | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| Konstruierbar | T | T | T | N | J | N | J | N | J | T | T | T | T | T | J | N | T | N | N | T | N | N | J | N | N |
| Eckenzahl | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| Konstruierbar | J | T | N | T | N | T | T | N | N | J | N | N | T | J | T | N | N | J | N | T | N | T | T | T | N |
| Eckenzahl | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| Konstruierbar | T | N | T | N | J | T | N | N | T | J | N | N | N | N | T | T | N | N | N | T | J | T | N | N | N |
| Eckenzahl | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| Konstruierbar | N | J | N | T | T | N | N | T | T | N | T | T | N | T | N | N | T | N | T | J | N | N | N | N | N |
| Eckenzahl | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| Konstruierbar | T | N | J | N | T | N | N | T | N | T | J | N | N | N | T | N | N | N | T | N | T | N | T | N | N |
| Eckenzahl | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| Konstruierbar | N | T | T | N | N | T | N | N | N | J | N | T | T | N | N | N | N | T | N | J | T | N | N | N | N |
| Eckenzahl | 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| Konstruierbar | N | N | N | N | T | N | T | N | N | T | N | N | N | T | T | N | J | T | T | T | N | N | N | N | N |
| Eckenzahl | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| Konstruierbar | N | N | N | J | N | N | N | T | N | T | N | N | N | N | N | T | N | T | T | N | T | T | N | T | N |
| Eckenzahl | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| Konstruierbar | N | N | T | N | N | N | N | N | T | N | N | N | T | N | J | N | N | T | N | N | N | T | N | N | N |
| Eckenzahl | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| Konstruierbar | N | T | N | N | J | J | J | N | T | T | N | N | N | N | N | T | N | N | N | T | N | J | T | N | N |
| Eckenzahl | 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| Konstruierbar | N | N | N | N | T | N | N | N | N | T | N | N | T | N | N | T | T | N | N | N | T | N | N | N | N |
| Eckenzahl | 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| Konstruierbar | N | N | N | T | N | T | N | N | N | N | N | T | N | N | T | N | N | N | N | J | N | N | T | T | N |
| Eckenzahl | 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| Konstruierbar | T | T | N | N | N | N | N | T | N | T | N | N | N | N | J | N | T | N | N | N | N | N | N | N | N |
| Eckenzahl | 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| Konstruierbar | T | N | N | N | N | N | T | N | N | T | N | N | N | T | T | N | N | N | N | T | N | N | N | N | N |
| Eckenzahl | 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| Konstruierbar | N | N | T | N | T | N | N | N | J | N | T | N | T | N | T | N | N | N | N | N | N | N | N | T | N |
| Eckenzahl | 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| Konstruierbar | N | N | N | N | T | N | N | J | N | N | N | N | N | N | N | T | N | N | N | T | N | N | N | N | N |
| Eckenzahl | 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| Konstruierbar | N | N | N | N | N | N | T | T | N | N | T | N | T | N | N | N | T | N | T | N | N | N | T | N | N |
| Eckenzahl | 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| Konstruierbar | N | N | N | N | T | T | N | N | T | N | N | N | N | N | N | N | N | T | N | N | N | N | N | N | N |
| Eckenzahl | 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| Konstruierbar | T | N | N | N | J | T | N | N | N | T | T | T | N | T | N | N | N | N | T | N | N | N | N | N | N |
| Eckenzahl | 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| Konstruierbar | N | N | N | T | N | N | N | N | N | J | T | J | T | J | N | N | N | T | N | T | N | N | N | N | N |
| Eckenzahl | 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| Konstruierbar | N | N | N | N | N | N | T | N | N | N | N | N | N | N | T | N | N | N | J | T | T | N | N | N | N |
| Eckenzahl | 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| Konstruierbar | N | N | N | N | T | N | N | N | N | T | N | N | N | N | N | N | T | N | N | T | N | N | N | N | N |
| Eckenzahl | 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| Konstruierbar | T | T | N | T | N | N | T | N | T | T | N | N | N | N | N | N | T | N | N | T | N | N | N | N | N |
| Eckenzahl | 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| Konstruierbar | N | N | N | N | N | N | N | T | N | N | N | T | N | N | N | N | N | N | N | N | N | N | N | T | N |
| Eckenzahl | 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| Konstruierbar | N | N | N | T | T | N | N | N | N | N | N | N | N | N | J | N | N | N | N | N | T | N | T | N | N |
| Eckenzahl | 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| Konstruierbar | N | T | N | T | N | N | T | N | N | N | N | N | T | N | T | T | N | N | N | N | N | T | N | N | N |
| Eckenzahl | 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| Konstruierbar | N | N | N | T | J | N | N | N | T | N | N | N | N | N | N | N | N | N | N | N | N | N | N | N | N |
| Eckenzahl | 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| Konstruierbar | N | T | T | N | N | N | N | N | N | N | N | N | N | T | N | N | N | N | N | T | N | N | N | N | N |
| Eckenzahl | 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| Konstruierbar | N | N | T | T | T | N | N | N | N | N | N | N | N | N | T | T | N | N | N | N | N | N | N | N | N |
| Eckenzahl | 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| Konstruierbar | N | N | N | N | N | T | N | N | N | T | N | N | T | N | T | N | N | J | T | N | J | T | N | N | N |
| Eckenzahl | 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| Konstruierbar | T | T | N | N | T | N | N | N | N | N | N | N | N | N | N | N | N | N | N | N | N | N | T | N | N |
| Eckenzahl | 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 | 810 | 811 | 812 | 813 | 814 | 815 | 816 | 817 | 818 | 819 | 820 | 821 | 822 | 823 | 824 | 825 |
| Konstruierbar | N | N | N | N | N | N | N | N | N | T | N | N | N | N | T | J | N | N | T | N | N | N | N | N | N |
| Eckenzahl | 826 | 827 | 828 | 829 | 830 | 831 | 832 | 833 | 834 | 835 | 836 | 837 | 838 | 839 | 840 | 841 | 842 | 843 | 844 | 845 | 846 | 847 | 848 | 849 | 850 |
| Konstruierbar | N | N | N | N | N | N | T | N | N | N | N | N | N | N | T | N | N | N | N | N | N | N | N | N | N |
| Eckenzahl | 851 | 852 | 853 | 854 | 855 | 856 | 857 | 858 | 859 | 860 | 861 | 862 | 863 | 864 | 865 | 866 | 867 | 868 | 869 | 870 | 871 | 872 | 873 | 874 | 875 |
| Konstruierbar | N | N | N | N | T | N | N | N | N | N | N | N | N | T | N | T | N | N | N | N | N | T | T | N | N |
| Eckenzahl | 876 | 877 | 878 | 879 | 880 | 881 | 882 | 883 | 884 | 885 | 886 | 887 | 888 | 889 | 890 | 891 | 892 | 893 | 894 | 895 | 896 | 897 | 898 | 899 | 900 |
| Konstruierbar | T | N | N | N | N | N | N | N | T | N | N | N | T | N | N | N | N | N | N | N | T | N | N | N | N |
| Eckenzahl | 901 | 902 | 903 | 904 | 905 | 906 | 907 | 908 | 909 | 910 | 911 | 912 | 913 | 914 | 915 | 916 | 917 | 918 | 919 | 920 | 921 | 922 | 923 | 924 | 925 |
| Konstruierbar | N | N | N | N | N | N | N | N | N | T | N | T | N | N | N | N | N | T | N | N | N | N | N | N | N |
| Eckenzahl | 926 | 927 | 928 | 929 | 930 | 931 | 932 | 933 | 934 | 935 | 936 | 937 | 938 | 939 | 940 | 941 | 942 | 943 | 944 | 945 | 946 | 947 | 948 | 949 | 950 |
| Konstruierbar | N | N | N | N | N | N | N | N | N | N | T | N | N | N | N | N | N | N | N | T | N | N | N | T | N |
| Eckenzahl | 951 | 952 | 953 | 954 | 955 | 956 | 957 | 958 | 959 | 960 | 961 | 962 | 963 | 964 | 965 | 966 | 967 | 968 | 969 | 970 | 971 | 972 | 973 | 974 | 975 |
| Konstruierbar | N | T | N | N | N | N | N | N | N | J | N | T | N | N | T | N | N | N | T | T | N | T | N | T | N |
| Eckenzahl | 976 | 977 | 978 | 979 | 980 | 981 | 982 | 983 | 984 | 985 | 986 | 987 | 988 | 989 | 990 | 991 | 992 | 993 | 994 | 995 | 996 | 997 | 998 | 999 | 1000 |
| Konstruierbar | N | N | T | N | N | T | N | N | N | N | N | N | T | N | N | N | N | N | N | N | N | N | N | T | N |
Eckenzahlen konstruierbarer Polygone findet man auch in der Folge A003401 in OEIS, Eckenzahlen nicht klassisch konstruierbarer Polygone in der Folge A004169 in OEIS.
Galoistheorie
Durch Entwicklung der Galoistheorie gelangte man zu einer tieferen Einsicht in das Problem. Die Menge der konstruierbaren Zahlen bildet nämlich einen Körper, in dem zusätzlich auch aus positiven Zahlen die Quadratwurzel gezogen werden kann. Insbesondere entspricht das Schneiden von Geraden dem Lösen einer linearen Gleichung und das Schneiden einer Geraden mit einem Kreis oder das Schneiden zweier Kreise dem Lösen einer quadratischen Gleichung. In der Sprache der Körpererweiterungen ist das folgende Tatsache:
- Ist eine konstruierbare Zahl, so gibt es einen Körperturm , so dass und für ein .
Umgekehrt ist natürlich auch jede Zahl aus konstruierbar. Ist also konstruierbar, so ist algebraisch und es ist eine Potenz von 2.
Zur Klärung der Konstruktion von regelmäßigen -Ecken mit betrachtet man Kreisteilungskörper als Körpererweiterung über , wobei die -te Einheitswurzel bezeichnet. Die -ten Einheitswurzeln sind die auf dem Einheitskreis liegenden Ecken eines regelmäßigen -Ecks. Es genügt die reelle Zahl zu konstruieren.
Sind zum Beispiel und teilerfremd, so ist . Sind dann das - und das -Eck konstruierbar, so ist auch das -Eck konstruierbar.
Um nun obige Argumente anwenden zu können, müssen einige Körpererweiterungsgrade bestimmt werden. Da die Kreisteilungspolynome irreduzibel sind, ist . Wegen ist , also ist , und damit .
Im regelmäßigen -Eck beträgt der Zentriwinkel . Ist somit das regelmäßige -Eck konstruierbar, so auch eine Strecke der Länge . Wegen ist dann auch diese Zahl konstruierbar, also muss eine Potenz von 2 sein. Damit ist dann .
Ist umgekehrt , so ist eine endliche abelsche Gruppe der Ordnung . Nach dem Hauptsatz über endlich erzeugte abelsche Gruppen existiert dann eine Kette von sukzessiven Normalteilern mit . Mit dem Hauptsatz der Galoistheorie erhält man daraus dann als Fixkörper von einen Körperturm mit , mithin ist für , und somit ist und damit auch das regelmäßige -Eck konstruierbar.
Sei beispielsweise . Dann ist eine Potenz von 2 und , da 2 eine Primitivwurzel modulo 5 ist. Eine mögliche Kette von Normalteilern ist . Der dazugehörige Körperturm ist . Es ist , da es normiert ist und annulliert und mit Reduktion modulo 2 irreduzibel ist. Nach Lösen der Gleichung ergibt sich . Nun könnte man bereits die erste Ecke konstruieren, indem man den Punkt mit Abstand vom Mittelpunkt auf einer Achse aus konstruiert und dann das Lot durch diesen Punkt fällt. Durch Lösen von ergibt sich . Durch diesen algebraischen Ausdruck lässt sich alternativ die erste Ecke konstruieren, indem man eine reelle und eine imaginäre Achse einzeichnet und mit deren Hilfe den Punkt konstruiert.
Einzelnachweise
- ↑ Edmund Weitz: Das regelmäßige 17-Eck. In: YouTube. 2017, abgerufen am 27. August 2020.
- ↑ George E. Martin: Geometric Constructions (= Undergraduate Texts in Mathematics). Springer-Verlag, New York 1998, ISBN 0-387-98276-0, S. 46, doi:10.1007/978-1-4612-0629-3.
- ↑ Folge A045544 in OEIS
- ↑ Heike Ernestus: Was steckt im Göttinger Koffer? Allgemein, CampusLeben/26. Juli 2021. Göttingen Campus, abgerufen am 7. Juni 2024.
- ↑ J. Hermes: Ueber die Teilung des Kreises in 65537 gleiche Teile. (PDF) Nachrichten von der Königl. Gesellschaft der Wissenschaften zu Göttingen Mathematisch-physikalische Klasse. SUB, Göttinger Universität Göttinger Digitalisierungszentrum, S. 170–186, abgerufen am 29. Mai 2023.
- ↑ Andrew Gleason: Angle Trisection, the Heptagon, and the Triskaidecagon. In: The American Mathematical Monthly. Band 95, Nr. 3, 1988, S. 185–194 (Seite 186, Fig. 1. Construction of a regular heptagon (Siebeneck). PDF sowie Seite 193, Fig. 4. Construction of a regular triskaidecagon (Dreizehneck). PDF ( vom 19. Dezember 2015 im Internet Archive)).Angle Trisection, the Heptagon, and the Triskaidecagon ( vom 2. Februar 2016 im Internet Archive) Original aus dem Archiv regeneriert am 31. Januar 2016
Siehe auch
Weblinks
- Konstruktion einer Dezimalzahl
- Eric W. Weisstein: Constructible Polygon. In: MathWorld (englisch).
- Triskaidecagon, Dreizehneck (engl. Wikipedia)
Auf dieser Seite verwendete Medien
Animation detailing the construction of a regular pentagon. The first part depicts the procedure to select a first point and then partitioning the circle with helper lines. After that a second point of the pentagon gets determined. Then it shows the procedure to find all other points. Based on the construction method as described by Richmond (1893) on the Pentagon page at MathWorld. Constructed using GeoGebra and animated using Adobe ImageReady CS2.
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Anwendungsbeispiel des Höhensatzes.
Durch die Ergänzung der konstruierten Strecke AB = a mit der Strecke BC = 1 ist mittels Thaleskreis konstruierbar.