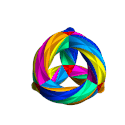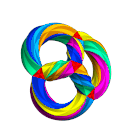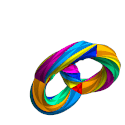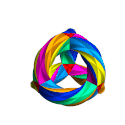Kleinsche Quartik

Die Kleinsche Quartik ist eine Kurve 4. Grades in der komplexen projektiven Ebene, die in homogenen Koordinaten ${\displaystyle (x,y,z)}$ durch die Gleichung

${\displaystyle x^{3}y+y^{3}z+z^{3}x=0}$

gegeben ist.

Sie wurde 1879 durch Felix Klein^[1] eingeführt und besitzt außergewöhnliche Symmetrieeigenschaften. Der algebraischen Kurve entspricht eine Riemannsche Fläche.

Die Symmetrieeigenschaften ergeben sich durch Parkettierung der hyperbolischen Ebene mit Heptagonen, so dass genau drei an jeder Ecke zusammenstoßen (deshalb ${\displaystyle \lbrace 7,3\rbrace }$ genannt). Aus genau 24 dieser Heptagone lässt sich ein Torus mit 3 Löchern bilden, die Kleinsche Fläche, topologisch vom Geschlecht 3. Es gibt 24 Transformationen der Parkettierung mit 24 Heptagonen ineinander und für jede noch 7 Drehungen des Heptagons, was 168 Symmetrieoperationen ergibt (mit Spiegelungen doppelt so viele, 336). Unterteilt man die Heptagone in Dreiecke erhält man die zu ${\displaystyle \lbrace 7,3\rbrace }$ (Poincaré-)duale Parkettierung ${\displaystyle \lbrace 3,7\rbrace }$ (an jeder Ecke stoßen 7 Dreiecke zusammen) und man kann die Fläche zur Klein-Quartik auch aus 56 Dreiecken dieser Parkettierung bilden. 56 Transformationen der Dreiecke in andere Dreiecke und jeweils drei Drehungen ergibt wieder 168 Transformationen.

Das ist auch gleichzeitig die maximale Anzahl von Symmetrien für Flächen vom Geschlecht 3, wie Adolf Hurwitz zeigte (Satz von Hurwitz über Automorphismengruppen): Eine Riemannsche Fläche vom Geschlecht ${\displaystyle g}$ hat maximal ${\displaystyle 84(g-1)}$ konforme Transformationen (ohne Spiegelungen). Die konformen Abbildungen lassen sich durch gebrochen-lineare Abbildungen (Möbiustransformationen) darstellen und bilden die projektive spezielle lineare Gruppe ${\displaystyle \operatorname {PSL} (2,\mathbb {C} )}$. Sie besteht aus komplexen 2×2-Matrizen mit Determinante 1, wobei Matrizen ${\displaystyle A}$ und ${\displaystyle -A}$ identifiziert werden.

Betrachtet man die hyperbolische Ebene als komplexe obere Halbebene ${\displaystyle \mathbb {H} }$, auf der ${\displaystyle \operatorname {PSL} (2,\mathbb {Z} )}$ wirkt, so ist die Riemannsche Fläche zur Klein-Quartik gegeben durch

${\displaystyle \mathbb {H} /\Gamma (7)}$

mit der Kongruenzuntergruppe

${\displaystyle \Gamma (7)=\left\{{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in {\text{PSL}}(2,\mathbb {Z} ):c\equiv b\equiv 0,a\equiv d\equiv 1{\pmod {7}}\right\}.}$

Sie ist eine Modulkurve (mit Geschlecht 3 und 24 Spitzen, siehe Modulform).

Ihre Symmetriegruppe ist ${\displaystyle \operatorname {PSL} (2,\mathbb {Z} )/\Gamma (7)=\operatorname {PSL} (2,\mathbb {Z} /7)}$ und hat 168 Elemente (ohne Reflexionen, die die komplexe Struktur nicht erhalten würden). Sie ist auch die Symmetriegruppe der Fano-Ebene und die zweitkleinste einfache nichtabelsche Gruppe. Noch kleiner ist nur die Ikosaedergruppe ${\displaystyle \operatorname {PSL} (2,\mathbb {Z} /5)}$ die Felix Klein in Zusammenhang mit der Gleichung fünften Grades und der Symmetriegruppe des Ikosaeders behandelte (sie hat 60 Elemente).

Da ihre Symmetriegruppe nicht in die dreidimensionale Drehgruppe SO(3) eingebettet werden kann, gibt es auch keine dreidimensionalen Realisierungen der Klein-Quartik, es gibt aber Darstellungen ihrer Form, zum Beispiel eine Skulptur von Helaman Ferguson vor dem MSRI in Berkeley.

Literatur

• Silvio Levy (Hrsg.): The Eightfold Way: The Beauty of Klein’s Quartic Curve, Cambridge UP 1999, Online

Weblinks

• John Baez, Klein’s Quartic Curve
• Klein Quartic, Mathworld

Einzelnachweise

1. ↑ Klein, Über die Transformationen siebenter Ordnung der elliptischen Funktionen, Mathematische Annalen, Band 14, 1879, S. 428–471, Nachdruck in den Gesammelten Abhandlungen, Springer, Band 3, S. 90–136, Digitalisat, Sub Göttingen