Kühlrippe

Kühlrippen (auch Kühllamellen oder Kühlfinnen genannt, engl. cooling fins) dienen zur Vergrößerung der Oberfläche eines Körpers, um die Wärmeübertragung an die Umgebung und damit die Kühlung zu verbessern. Gerippte Oberflächen können dabei Teil der wärmeerzeugenden Maschine selbst sein, etwa an einem Motorblock, oder auch als davon getrenntes Bauteil ausgeführt werden. Solche Kühlkörper können wiederum in direktem mechanischen Kontakt mit der Wärmequelle stehen oder über ein zusätzliches Medium mit ihr verbunden werden, wie es beispielsweise bei der Wasserkühlung praktiziert wird. Kühlkörper sorgen passiv oder als Teil einer aktiven Kühlung für die Einhaltung einer zulässigen Betriebstemperatur von Maschinen, elektrischen und elektronischen Systemen.

Erfunden und erstmals verwendet wurde die Kühlrippe vom österreichischen Ingenieur Franz Pichler zur Kühlung von Trockentrafos.^[1][2]

Der Wärmestrom von einer Oberfläche zum umgebenden Kühlmedium hängt von der Temperaturdifferenz, von der Kontaktfläche und vom Wärmeübergangskoeffizienten nach der folgenden Beziehung ab

${\displaystyle {\dot {Q}}=h\cdot A\cdot (T_{1}-T_{u})}$

mit

${\displaystyle {\dot {Q}}}$ = Wärmestrom [W]

${\displaystyle h}$ = Wärmeübergangskoeffizient [W/(m²·K)]

${\displaystyle A}$ = Kontaktfläche [m²]

${\displaystyle T_{1}}$ = Temperatur des Körpers [°C]

${\displaystyle T_{u}}$ = Temperatur des Kühlmediums [°C]

Durch Vergrößerung der Kontaktfläche A kann also die abgeführte Wärmemenge erhöht werden. Der Wärmestrom erhöht sich jedoch nicht proportional zur Flächenvergrößerung, sondern ist abhängig vom Rippenwirkungsgrad (siehe unten).

Die Rippen bedeuten eine – meist unerwünschte – Erhöhung des Gewichtes und der äußeren Abmessungen. Sie können beim gezielten Einsatz neben der Kühlung jedoch auch die mechanische Festigkeit eines Bauteiles erhöhen oder die Schallabstrahlung einer Maschine reduzieren (durch Unterdrücken von Oberflächenschwingungen).

Bei konstanter Wärmeleitung entlang eines Stabes oder einer Rippe stellt sich ein thermisches Gleichgewicht ein zwischen dem Wärmestrom, der in den Stab eintritt, und dem Wärmestrom, der über die Oberfläche an die Umgebung abgeführt wird.

Im Folgenden betrachten wir den mathematisch einfachsten Fall: ein Stab oder eine Rippe mit einem rechteckigen Querschnitt, eine konstante Umgebungstemperatur und ein konstanter Wärmeübergangskoeffizient. Betrachtet man das Stabelement dx, so ergibt sich folgende Gleichgewichtsbedingung:

Eintretender Wärmestrom:

${\displaystyle {\dot {Q}}_{x}=-\lambda \cdot A\cdot {\frac {dT}{dx}}}$

Austretender Wärmestrom:

${\displaystyle {\begin{alignedat}{2}{\dot {Q}}_{x+dx}&={\dot {Q}}_{x}&&-{\frac {d{\dot {Q}}}{dx}}\cdot dx\\&=-\lambda \cdot A\cdot {\frac {dT}{dx}}&&+\lambda \cdot A\cdot {\frac {d^{2}T}{dx^{2}}}\cdot dx\end{alignedat}}}$

Der Wärmeübergang an der Oberfläche zur Umgebung beträgt:

${\displaystyle d{\dot {Q}}=h\cdot U\cdot dx\cdot (T-T_{u})}$

hier bedeuten:

${\displaystyle h}$ = Wärmeübergangskoeffizient [W/m²·K]

${\displaystyle U}$= Umfang der Rippe [m]

${\displaystyle A}$ =Rippenquerschnitt [m²]

${\displaystyle \lambda }$ = Wärmeleitfähigkeit des Werkstoffes [W/K·m]

${\displaystyle T_{u}}$ = Umgebungstemperatur [°C]

Aus der Wärmebilanz ergibt sich:

${\displaystyle {\dot {Q}}_{x}-{\dot {Q}}_{x+dx}={\frac {d{\dot {Q}}}{dx}}\cdot dx=d{\dot {Q}}}$

Dies führt zu der Differentialgleichung für die Rippentemperatur:

${\displaystyle \Rightarrow {\frac {d^{2}T}{dx^{2}}}=m^{2}\cdot (T-T_{u})}$

Hier bedeuten:

ΔT = T – T_u

${\displaystyle m={\sqrt {\frac {h\cdot U}{\lambda \cdot A}}}}$

Die Lösung der Differentialgleichung führt zu folgenden Ergebnissen (der Wärmestrom durch die Stirnfläche am Rippenende wird vernachlässigt):

Temperaturverlauf entlang der Rippe:

${\displaystyle \Delta T(x)=\Delta T_{1}\cdot {\frac {\cosh(m\cdot (L-x))}{\cosh(m\cdot L)}}}$

Temperatur am Rippenende:

${\displaystyle \Delta T_{2}=\Delta T(x=L)=\Delta T_{1}\cdot {\frac {1}{\cosh(m\cdot L)}}}$

Mit

${\displaystyle {\frac {dT}{dx}}=\Delta T_{1}\cdot m\cdot {\frac {\sinh(m\cdot (L-x))}{\cosh(m\cdot L)}}}$

folgt der Wärmestrom durch die Grundfläche der Rippe:

${\displaystyle \Rightarrow {\dot {Q}}_{1}={\dot {Q}}(x=0)=m\cdot \lambda \cdot A\cdot \Delta T_{1}\cdot \tanh(m\cdot L)}$

Hier bedeuten:

L= Länge der Rippe

ΔT₁ =Rippenübertemperatur an der Rippenbasis

sinh, cosh, tanh: Hyperbelfunktionen

Die Kühlwirkung einer Rippe nimmt also mit steigendem Temperaturabfall von der Rippenbasis zu Rippenspitze ab. Maßgeblich für diesen Temperaturabfall ist nach den obigen Gleichungen die dimensionslose Kenngröße (m  · L).

Beispiel

Im nebenstehenden Bild ist die (auf 1 normierte) Rippenübertemperatur ΔT an einer Rippe der Länge L für verschiedene Werte der Kenngröße (m  · L) dargestellt. Die Kenngrößen (m  · L) wurden für eine 0,5 mm starke und 30 mm hohe rechteckige Rippe (A = 15 mm²; U = 61 mm) aus vier unterschiedlichen Materialien im Luftstrom bei einem Wärmeübergangskoeffizienten h = 15 W/m²/K berechnet. Bei den Kupfer- und Aluminiumrippen (m  · L = 0,37 bzw. 0,52) beträgt der Temperaturabfall zu Rippenspitze weniger als 10 %, diese Rippen haben eine nahezu ideale Kühlwirkung. Bei der Kunststoffrippe (m  · L = 14) fällt jedoch bereits nach einem Viertel der Länge (L/4) die Rippenübertemperatur auf weniger als 5 % des Anfangswertes, diese Rippe ist für die Kühlung praktisch unwirksam.

Der Rippenwirkungsgrad ist definiert als das Verhältnis des Wärmestroms ${\displaystyle {\dot {Q}}_{1}}$, den die Rippe tatsächlich abgibt, zum idealen Wärmestrom ${\displaystyle {\dot {Q}}_{\mathrm {ideal} }}$, den die Rippe abgeben würde, wenn sie über ihre gesamte Länge die Anfangstemperatur T₁ besäße (bei einer unendlich hohen Wärmeleitfähigkeit):

${\displaystyle \eta _{R}={\frac {{\dot {Q}}_{1}}{{\dot {Q}}_{\mathrm {ideal} }}}={\frac {\int \limits _{0}^{L}h\cdot \Delta T_{(x)}\cdot U\cdot dx}{h\cdot \Delta T_{1}\cdot U\cdot L}}}$

mit

• h = Wärmeübergangskoeffizient [W/m² K]
• U = Umfang der Rippe [m]
• L = Länge der Rippe [m].

Für eine rechteckige Rippe, einen konstanten Wärmeübergangskoeffizient und eine konstante Umgebungstemperatur wurde oben abgeleitet:

${\displaystyle {\dot {Q}}_{1}=m\cdot \lambda \cdot A\cdot \Delta T_{1}\cdot \tanh(m\cdot L)}$

Damit errechnet sich der Rippenwirkungsgrad zu:

${\displaystyle \Rightarrow \eta _{R}={\frac {\tanh(m\cdot L)}{m\cdot L}}}$

mit

• dem Kennwert ${\displaystyle m={\sqrt {\frac {h\cdot U}{\lambda \cdot A}}}}$ in [1/m]
• ${\displaystyle \tanh }$ Tangens hyperbolicus.

Beispiel: Einfluss der Rippendicke auf den Wirkungsgrad

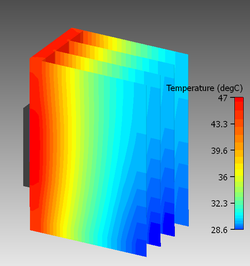
Die unten stehenden Bilder zeigen die berechnete Temperaturverteilung an zwei Aluminium-Kühlkörpern. Durch Erhöhung der Rippendicke von 0,2 mm (Bild links) auf 2,0 mm (Bild rechts) wurde der Temperaturabfall zu Rippenspitze deutlich verkleinert und der Rippenwirkungsgrad erhöht.

• 
  Kühlrippen mit einem niedrigen Wirkungsgrad
• 
  Kühlrippen mit einem hohen Wirkungsgrad

Eine höhere Rippendichte führt zu einer Vergrößerung der Wärmeabgabefläche und damit zu einer höheren Effizienz für die Kühlung. Auf der anderen Seite hat eine höhere Rippendichte engere Rippenkanäle mit einem wachsenden Strömungswiderstand zur Folge. Das führt zu einem sog. by-pass Effekt: Die strömende Luft wird aus den Rippenkanälen 'verdrängt’ und strömt in zunehmendem Maße ungenutzt an der Verrippung vorbei. Die Ursache liegt in der Wandreibung mit der Bildung einer Strömungsgrenzschicht. Die Dicke der Grenzschicht ist abhängig von der Reynoldszahl, siehe auch Grenzschichtgleichungen. Eine numerische Simulation dieses by-pass Effektes zeigen die zwei unten stehenden Bilder.

• 
  Luftströmung durch einen Kühlkörper mit ausreichendem Rippenabstand
• 
  Luftströmung durch einen Kühlkörper mit zu geringem Rippenabstand

• Walter Wagner: Wärmeübertragung. 6. Auflage. Vogel Buchverlag 2004, Kamprath Reihe, ISBN 3-8023-1974-5.
• Allan D. Kraus, Bar-Cohen Avram: Thermal Analysis and Control of Electronic Equipment. Hemisphere Publishing Corporation 1983, ISBN 0-07-035416-2.
• D. Q. Kern, A. D. Kraus: Extended Surface Heat Transfer. McGraw-Hill, New York 1972, ISBN 0-07-034195-8.

• Estimating Parallel Plate-Fin Heat Sink Thermal Resistance
• Einführung in die Physik der Entwärmung elektronischer Systeme (PDF-Datei; 358 kB)
• Vorlesung Universität der Bundeswehr München (PDF-Datei; 2,23 MB)

1. ↑ Deutsche Biographie – Pichler, Franz. In: deutsche-biographie.de. Abgerufen am 15. August 2016. 
2. ↑ Biographie aus dem Österreichischen Biographischen Lexikon. (PDF) In: biographien.ac.at. Abgerufen am 15. August 2016.