Jamantau

Jamantau
Höhe	1640 m
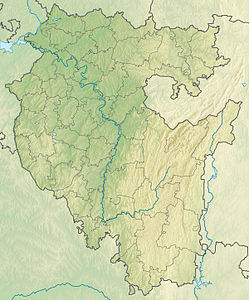
Lage	Baschkortostan (Russland)
Gebirge	Südlicher Ural
Koordinaten	54° 15′ 18″ N, 58° 6′ 7″ O54.25558.1021640
Erschließung	Militärisches Sperrgebiet, zivile Nebenstraßen im unmittelbaren Umland
Besonderheiten	Höchster Berg des Südural, Lage in baschkirischem Nationalpark

Die Jamantau (russisch Ямантау, Baschkirisch Ямантау — nutzloser oder schlechter Berg) ist mit 1640 m der höchste Berg des südlichen Ural. Er liegt in der zu Russland gehörenden Republik Baschkortostan unmittelbar an der Grenze zur Oblast Tscheljabinsk. In der Nähe des Bergs befindet sich das Naturreservat Schulgan-Tasch sowie die durch Steinzeitmalereien bekannte Höhle von Kapowa. Der Berg hat einen Doppelgipfel, neben dem Großen existiert auch noch der Kleine Jamantau (1510 m) als Nebengipfel.

Militärkomplex und Verschwörungstheorien

Berühmtheit erlangte der Jamantau in den USA infolge einer in konservativen Kreisen lancierten Verschwörungstheorie, nach der er als ein russisches Gegenstück zur legendären Area 51 angesehen wird. Nach dortigem Glauben beherbergt er einen riesigen unterirdischen Komplex aus der Breschnew-Ära, der monumentale Ausmaße hätte.

Gesichert ist die Existenz von Militäranlagen der russischen Armee bei den nahen geschlossenen Städten Meschgorje und Sneschinsk. Weiterhin soll es tatsächlich einen geheimen, atombombensicheren Bunker unter dem Berg geben.^[1] Nach US-Quellen soll der dortige Komplex Platz für 60.000 Personen bieten. Es soll dort auch Atomwaffen-Forschung betrieben werden.

Weblinks

Commons: Jamantau – Sammlung von Bildern, Videos und Audiodateien

• Film über die Region bei russland.TV (dt.)
• Artikel, Fotogalerie und Landkarte bei Southural.ru (russ.)
• Geheimnisse des Jamantau – Verschwörungstheorien (russ.)

Einzelnachweise

1. ↑ Viewzone: Yamantau: A Future Armageddon?