Interpolation (Fotografie)
Interpolation (wörtliche Übersetzung: „Zwischenrechnen“) bezeichnet in der digitalen Fotografie ein Verfahren zur Erzeugung von Bildinhalten
- zwischen verschiedenen Pixeln eines Bildes (Dichteinterpolation)
- innerhalb einzelner Pixel (Farbinterpolation).
Interpolation ist ein notwendiger Bestandteil des Signalverarbeitungsweges digitaler Bilder, da alle Änderungen an der Pixelmenge und der Farbe nur hiermit realisiert werden können. Im gesamten Verarbeitungsweg zwischen Bilderzeugung und -darstellung wird mehrfach interpoliert – dabei entsteht immer ein Schärfeverlust.
Grundlagen
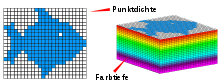
Jedes Pixel transportiert auf zwei Arten Bildinformationen:
- Im Zusammenspiel mit anderen Pixeln (nur alle Pixel zusammen ergeben ein Bild). Dies wird durch die Punktdichte dargestellt.
- Innerhalb des Pixel (Helligkeit & Farbe). Dies wird durch die Farbtiefe dargestellt.

In jeder Bildverarbeitungskette (Beispiel: Kamera – Bildschirm – Speicher – Drucker) wird die Punktdichte und Farbe jedes Bildes mehrfach geändert. Das ist u. a. durch die Anpassung des Bildes an das bilddarstellende Medium notwendig. Typisch dafür sind die Unterschiede zwischen Bildschirm und Drucker, da beide jeweils spezielle Punktdichten benötigen und unterschiedliche Farbräume benutzen.
Mittels Interpolation wird die Pixelmenge um den gewünschten Wert erhöht oder verringert, sowie bei Farb- und Helligkeitsänderungen der neue Farbwert ermittelt. Durch dieses Zwischenrechnen entstehen keine neuen Bildinformationen, sondern immer nur Zwischenwerte auf Basis der ursprünglichen Informationen.
Dichteinterpolation
Die Pixelmenge aller digitalen Bilder muss mehrfach geändert werden. Exemplarisch kann das am nebenstehenden Fischbild beobachtet werden:
- das Originalbild ist 800×300 Pixel groß
- in der Darstellung eines durchschnittlichen Internetbrowsers wird dieses Bild gerade mit ca. 216×82 Pixel angezeigt
- ein Ausdruck in 20 cm Breite bei 300dpi würde dagegen eine Menge von 2362×886 Pixeln notwendig machen.
Die Verringerung oder Erhöhung der Pixelmenge wird durch Interpolation erreicht.
- Beispiel für die Interpolation der Punktdichte:
Der Fisch im Musterbild besteht aus 25×20 Quadraten. Wie würde die Dichteinterpolation auf 17×13 Quadraten oder auf 27×21 Quadraten aussehen? Diese nicht-ganzzahligen Zwischenrechnungen stellen das Kernproblem aller Interpolationen dar und sind die Ursache für verschiedene Interpolationsmethoden.
- (c) JunK, CC BY-SA 3.0
Die linke Linie wurde durch die Interpolationsart Pixelwiederholung, die rechte Linie durch bikubische Interpolation errechnet.
Das Ergebnis ist links eine scharfe, aber lückenhafte Linie, rechts eine unscharfe, aber lückenarme Linie.
Farbinterpolation
Die Farb- und Helligkeitsinformationen von Pixeln werden gemeinsam in der Farbtiefe eines Bildes gespeichert. In der Bildverarbeitungskette werden die Farbinformationen eines digitalen Bildes mehrfach geändert (innerhalb der Farbtiefe). Exemplarisch kann das erneut am nebenstehenden Fischbild beobachtet werden:
- wird das Fischbild gedruckt, sieht die Farbe des Ausdrucks immer anders aus als die Darstellung der Farbe am Bildschirm
- jeder Bildschirm stellt (zumindest geringfügig) die Farbe des Fischbildes anders dar, als ein anderer Bildschirm
- Beispiel für die Interpolation der Farbe:
Ein digital fotografiertes Bild wird meist mit 3 Farbkanälen in Rot, Grün und Blau bearbeitet. Im häufigsten Fall besitzt jeder Farbkanal 256 Abstufungen (= 8bit). Wie würde eine Farbänderung im Fischbild aussehen, beispielsweise eine Halbierung der Helligkeit?
- der hellblaue Untergrund besitzt einen Cyanwert von 206; eine Halbierung ergibt 103
- der blaue Fisch besitzt einen Blauwert von 255; eine Halbierung ist hier nicht möglich, da die Farbkanäle nur ganzzahlige Abstufungen zulassen. Es hängt vom verwendeten Interpolationsverfahren ab, welcher neue Blauwert nach der Helligkeitsänderung vorhanden ist.
Das Farbspektrum des Fotos links umfasst ca. 200 Stufen (damit wird die Farbtiefe von 256 Stufen nicht komplett ausgenutzt). Im rechten Foto wurde eine einfache Kontrasterhöhung durchgeführt, die das Farbspektrum des Fotos auf 256 Stufen angehoben hat (= Tonwertspreizung). Die vorher-200 Stufen können nicht identisch auf nachher-256 Stufen übertragen werden. Die konkreten Farbwerte werden durch das Interpolationsverfahren bestimmt. Symbolisiert werden die (durch diese Veränderung) entstehenden Lücken im Farbspektrum durch eine lückenhafte Anzeige im Histogramm (Diagramm unter dem Foto).
Interpolationsmethoden
Aus mathematischer Sicht bedeutet Interpolation „Zwischenwertermittlung“. Dabei werden aus den bekannten Pixelwerten eines Bildes die neuen Werte mittels Interpolationsalgorithmen berechnet. Der wesentliche Unterschied bei den verschiedenen Interpolationsmethoden liegt in der Auswertung der bekannten Pixelwerte und der daraus resultierenden Festlegung der neuen Bildinhalte. Die Gemeinsamkeit aller Interpolationsmethoden ist Auswirkung auf den Inhalt von Punktdichte und Farbtiefe.
In jeder Bildverarbeitungskette wird oft mehrfach interpoliert. Dabei kommt es immer auch zu nicht-ganzzahligen Änderungen. Durch diese Art der Änderung entsteht ein Verlust an Information und damit ein Verlust an Schärfe. Durch diesen systembedingten Schärfeverlust dominiert bei der Wahl des Interpolationsverfahrens immer der Einfluss auf den Schärfeeindruck.
Der Schärfeeindruck bestimmt die Wahl des Interpolationsverfahrens:
In der Mitte sind zwei Versionen eines Gesichtes zu sehen. Die meisten Betrachter empfinden bei dem rechten Foto einen höheren Schärfeeindruck (weil kontrastreicher).
In den Vergrößerungen (außen) ist deutlich zu erkennen, dass das linke Bild mehr Schärfe (= mehr Detailreichtum) enthält. Schärfe und Schärfeeindruck sind zwei verschiedene Dinge.
Typische Interpolationsmethoden sind Pixelwiederholung, bilineare Interpolation und bikubische Interpolation. Diese basieren auf dem Verfahren eines Rekonstruktionsfilters.
Pixelwiederholung
Bei der Pixelwiederholung, auch Nearest neighbor („nächster Nachbar“) genannt, wird jedem Pixel des Ausgabebildes der Farbwert des nächstgelegenen Pixels des Eingabebildes zugewiesen. Bei der Verringerung von Punktdichten oder nicht-ganzzahligen Änderungen werden einige der vorhandenen Pixelwerte gelöscht. Die Verkleinerung von Bildern mit dieser Methode kann zu starken Alias-Effekten führen, die sich als Bildartefakte äußern. Bei der Vergrößerung mittels Pixelwiederholung kommt es zu einer klötzchenartigen, „pixeligen“ Darstellung.
Bilineare Interpolation
Bei der bilinearen Interpolation wird der Farbwert eines Pixels des Ausgabebildes aus den vier benachbarten Farbwerten des Eingabebildes interpoliert. Bei der Verringerung von Punktdichten oder nicht-ganzzahligen Änderungen werden dadurch einfache Wertetendenzen (Beispiel: starke Helligkeitsänderungen) berücksichtigt.
Bikubische Interpolation
Diese Methode benutzt analytische Funktionen (also die Berücksichtigung von Tendenzen über die Nachbarpixel hinaus) zur Neuberechnung. Dabei wird ein Farbwert des Ausgabebildes aus den benachbarten Farbwerten des Eingabebildes mittels kubischen Splines interpoliert. Es gibt mehrere gebräuchliche kubische Splines mit unterschiedlichen Eigenschaften; der Begriff „bikubische Interpolation“ ist daher mehrdeutig. Bei der Verringerung von Punktdichten oder nicht-ganzzahligen Änderungen entstehen hierbei deutlich „weichere“ Übergänge zwischen den neuen Pixeln als bei der einfachen Pixelwiederholung.
Das Bildbearbeitungsprogramm GIMP (Version 2.7) verwendet Catmull-Rom-Splines. Bei diesem Spline-Typ kommt es zum Überschwingen der Farbwerte an Kanten, was sich als Schärfung des Bildes äußert. Das Bildbearbeitungsprogramm Paint.NET (Version 3.36) hingegen verwendet kubische B-Splines, welche zu einer verschwommeneren Darstellung führen.
Vergleiche verschiedener Interpolationsverfahren
Vergleich bei Dichteinterpolationen
Vergrößerung durch Rekonstruktion mit einem separablen Catmull-Rom-Filter (bikubische Interpolation)
Vergrößerung durch Rekonstruktion mit einem separablen kubischen B-Spline-Filter (bikubische Interpolation)
Vergleich bei Farbinterpolationen
Die Originaldatei (jede Farbe ist 3×3 Pixel groß gewesen) wurde mittels Pixelwiederholung in einem ganzzahligen Verhältnis interpoliert -dabei entstehen keine Informationsveränderungen.
Der einzige Unterschied zum Originalbild (links) ist die mehrfache Halbierung und Verdopplung der Helligkeitswerte. Dieses enthält eine nicht-ganzzahlige Änderung, die sich als Farbänderung deutlich macht.
Die bikubische Interpolation der Originaldatei – deutlich sind die weicheren Übergänge erkennbar.
U. a. entsteht daraus auch eine Veränderung innerhalb der Farbtiefe (siehe Histogramm in der Mitte) – das bikubisch interpolierte Bild enthält deutlich weniger Lücken in der Tonwertverteilung als das durch Pixelwiederholung interpolierte Bild.Die bikubische Interpolation des darüberliegenden Bildes – die Unterschiede zum linken Bild entstehen durch die unterschiedlichen Ausgangswerte.
Weblinks
- Bildverarbeitung in der Praxis von Rainer Steinbrecher in der 2. überarbeiteten Auflage als Download-Version (PDF 6,1 MB) (1. Auflage: ISBN 3-486-22372-0) – u. a. Kapitel "Bildverbesserung" S. 122
Auf dieser Seite verwendete Medien
(c) Friedrich Graf at de.wikipedia, CC BY-SA 3.0
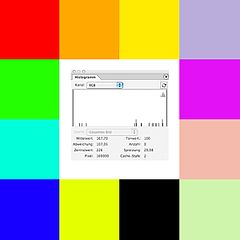
Die Hauptmerkmale von Rastergrafiken sind die Anzahl der Pixel und deren Farbtiefe. Wird die Anzahl der Pixel oder deren Farbe (bzw. Helligkeit) geändert, erfolgt dies durch Interpolation ("Zwischenrechnung").
Der Unterschied zwischen Datei 1a und 2a ist durch die Wiederholung einer einfachen Helligkeitsänderung (und dem zurücksetzten derselben) entstanden. Im Histogramm (Mitte des Bildes) sind deutlich die Lücken zwischen den Farben sichtbar.
Der Unterschied zwischen Datei 1a und 1b (sowie 2a und 2b) entsteht durch die Interpolationsmethode "bikubisch". Bei ihr werden auch die Nachbarpixel in die Zwischenrechnung einbezogen. Durch diese Interpolation wurden die Lücken zwischen den einzelnen Farben gefüllt (siehe Histogramm in der Mitte).
Der Unterschied zwischen 1b und 2b entsteht durch die Kombination von unterschiedlichem Ausgangsbild und der bikubischen Interpolation.
Skalierung mittels bikubischer Interpolation eines 4x4-Pixel-Musters (Image:SourceInterpolationExample2.png) auf 25600 % der Ausgangsgröße.
Autor/Urheber:
Friedrich Graf
, Lizenz: CC-by-sa 2.0/deFarbverluste durch Kontraständerung.
Image resampling by interpolation
Autor/Urheber: Jeff Dahl, Lizenz: CC BY-SA 3.0
Example of Inkscape's interpolation command
(c) Friedrich Graf at de.wikipedia, CC BY-SA 3.0
Die Hauptmerkmale von Rastergrafiken sind die Anzahl der Pixel und deren Farbtiefe. Wird die Anzahl der Pixel oder deren Farbe (bzw. Helligkeit) geändert, erfolgt dies durch Interpolation ("Zwischenrechnung").
Der Unterschied zwischen Datei 1a und 2a ist durch die Wiederholung einer einfachen Helligkeitsänderung (und dem zurücksetzten derselben) entstanden. Im Histogramm (Mitte des Bildes) sind deutlich die Lücken zwischen den Farben sichtbar.
Der Unterschied zwischen Datei 1a und 1b (sowie 2a und 2b) entsteht durch die Interpolationsmethode "bikubisch". Bei ihr werden auch die Nachbarpixel in die Zwischenrechnung einbezogen. Durch diese Interpolation wurden die Lücken zwischen den einzelnen Farben gefüllt (siehe Histogramm in der Mitte).
Der Unterschied zwischen 1b und 2b entsteht durch die Kombination von unterschiedlichem Ausgangsbild und der bikubischen Interpolation.
Image resampling using bilinear interpolation
Skalierung mittels Nutzung des nächsten Nachbars eines 4x4-Pixel-Musters (Image:SourceInterpolationExample2.png) auf 25600 % der Ausgangsgröße.
Autor/Urheber:
Friedrich Graf
, Lizenz: CC-by-sa 2.0/deSchärfe und Schärfeeindruck sind zweierlei.
Autor/Urheber:
Gerard Pons, Ergänzung Friedrich Graf
, Lizenz: PD-SchöpfungshöheBeispiel für die Erhöhung der Punktdichte mittels Interpolation.
Skalierung mittels bilinearer Interpolation eines 4x4-Pixel-Musters (Image:SourceInterpolationExample2.png) auf 25600 % der Ausgangsgröße.
(c) JunK, CC BY-SA 3.0
Antialiasing
Die linke Linie wurde durch die Interpolationsart Pixelwiederholung, die rechte Linie durch bikubische Interpolation errechnet.
Das Ergebnis ist links eine scharfe, aber lückenhafte Linie, rechts eine unscharfe, aber lückenarme Linie.(c) Friedrich Graf at de.wikipedia, CC BY-SA 3.0
Die Hauptmerkmale von Rastergrafiken sind die Anzahl der Pixel und deren Farbtiefe. Wird die Anzahl der Pixel oder deren Farbe (bzw. Helligkeit) geändert, erfolgt dies durch Interpolation ("Zwischenrechnung").
Der Unterschied zwischen Datei 1a und 2a ist durch die Wiederholung einer einfachen Helligkeitsänderung (und dem zurücksetzten derselben) entstanden. Im Histogramm (Mitte des Bildes) sind deutlich die Lücken zwischen den Farben sichtbar.
Der Unterschied zwischen Datei 1a und 1b (sowie 2a und 2b) entsteht durch die Interpolationsmethode "bikubisch". Bei ihr werden auch die Nachbarpixel in die Zwischenrechnung einbezogen. Durch diese Interpolation wurden die Lücken zwischen den einzelnen Farben gefüllt (siehe Histogramm in der Mitte).
Der Unterschied zwischen 1b und 2b entsteht durch die Kombination von unterschiedlichem Ausgangsbild und der bikubischen Interpolation.
Image resampling using nearest neighbor interpolation
Image resampling using a separable Catmull-Rom filter
(c) Friedrich Graf at de.wikipedia, CC BY-SA 3.0
Die Hauptmerkmale von Rastergrafiken sind die Anzahl der Pixel und deren Farbtiefe. Wird die Anzahl der Pixel oder deren Farbe (bzw. Helligkeit) geändert, erfolgt dies durch Interpolation ("Zwischenrechnung").
Der Unterschied zwischen Datei 1a und 2a ist durch die Wiederholung einer einfachen Helligkeitsänderung (und dem zurücksetzten derselben) entstanden. Im Histogramm (Mitte des Bildes) sind deutlich die Lücken zwischen den Farben sichtbar.
Der Unterschied zwischen Datei 1a und 1b (sowie 2a und 2b) entsteht durch die Interpolationsmethode "bikubisch". Bei ihr werden auch die Nachbarpixel in die Zwischenrechnung einbezogen. Durch diese Interpolation wurden die Lücken zwischen den einzelnen Farben gefüllt (siehe Histogramm in der Mitte).
Der Unterschied zwischen 1b und 2b entsteht durch die Kombination von unterschiedlichem Ausgangsbild und der bikubischen Interpolation.
Autor/Urheber: , Lizenz: CC-by-sa 3.0/de
Punktdichte und Farbtiefe bilden die Matrix jeder Rastergrafik. Damit bestimmen sie das theoretisch erreichbare Qualitätsmaximum. Die praktisch erreichbare Qualität wird bestimmt von dem tatsächlichen Informationsgehalt (Schärfe) und dem virtuellen Informationsgehalt (Schärfeeindruck).
Image resampling using a separable cubic B-spline filter