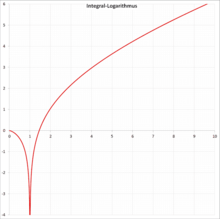
Funktionsgraph von li ( x ) {\displaystyle \operatorname {li} (x)} Der Integrallogarithmus ist eine analytische Funktion auf den reellen Zahlen x ≥ 0 , x ≠ 1 {\displaystyle x\geq 0,\;x\neq 1} x > 1 {\displaystyle x>1} Quantenfeldtheorie und bei der Lösung der Laplace-Gleichung in Halbleitern sowie in der Zahlentheorie , da sie eng mit der Dichte der Primzahlen verknüpft ist.
Definition Es sind zwei Definitionen üblich, die sich um eine Konstante unterscheiden. Für eine der wichtigsten Anwendungen – als asymptotische Vergleichsgröße für die Primzahlfunktion im Primzahlsatz – spielt der Unterschied zwischen den beiden Definitionen keine Rolle.
Eine Definition im Bereich x ≥ 0 {\displaystyle x\geq 0}
li ( x ) = ∫ 0 x d t ln t , {\displaystyle \operatorname {li} (x)=\int _{0}^{x}{\frac {\mathrm {d} t}{\ln t}}\ ,} dabei muss li {\displaystyle \operatorname {li} } Polstelle bei x = 1 {\displaystyle x=1} x > 1 {\displaystyle x>1} Grenzwert definiert werden (cauchyscher Hauptwert ):
li ( x ) = lim ε → 0 + ( ∫ 0 1 − ε d t ln t + ∫ 1 + ε x d t ln t ) . {\displaystyle \operatorname {li} (x)=\lim _{\varepsilon \to 0^{+}}\left(\int _{0}^{1-\varepsilon }{\frac {\mathrm {d} t}{\ln t}}+\int _{1+\varepsilon }^{x}{\frac {\mathrm {d} t}{\ln t}}\right)\ .} Eine andere Definition für x > 1 {\displaystyle x>1}
Li ( x ) = li ( x ) − li ( 2 ) = ∫ 2 x d t ln t . {\displaystyle \operatorname {Li} (x)=\operatorname {li} (x)-\operatorname {li} (2)=\int _{2}^{x}{\frac {\mathrm {d} t}{\ln t}}\ .} Bei x = 1 {\displaystyle x=1} logarithmische Singularität vor.
Eigenschaften Funktionsgraph von li ( x ) {\displaystyle \operatorname {li} (x)} Einige Werte:
li ( 0 ) = 0 {\displaystyle \operatorname {li} (0)=0} li ( 1 ) = − ∞ {\displaystyle \operatorname {li} (1)=-\infty } li ( μ ) = 0 {\displaystyle \operatorname {li} (\mu )=0} li ( 2 ) = 1,045 16 37801 17492 78484 … {\displaystyle \operatorname {li} (2)=1{,}04516\;37801\;17492\;78484\ldots } A069284 in OEIS )Dabei ist μ = 1,451 36 92348 83381 05028 … {\displaystyle \mu =1{,}45136\;92348\;83381\;05028\ldots } A070769 in OEIS ) die Ramanujan-Soldner-Konstante .
Es gilt li ( x ) = Ei ( ln x ) {\displaystyle \operatorname {li} (x)=\operatorname {Ei} (\ln x)} Integralexponentialfunktion Ei {\displaystyle \operatorname {Ei} }
li ( x ) = γ + ln | ln x | + ∑ k = 1 ∞ ( ln x ) k k ⋅ k ! , {\displaystyle \operatorname {li} (x)=\gamma +\ln \left|\ln x\right|+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k\cdot k!}}\ ,} wobei γ = 0,577 21 56649 01532 86060 … {\displaystyle \gamma =0{,}57721\;56649\;01532\;86060\ldots } A001620 in OEIS ) die Euler-Mascheroni-Konstante ist.
Aus der Definition von li {\displaystyle \operatorname {li} } lineare Substitution
li ( x ) = x ∫ 0 1 d t ln ( x t ) , {\displaystyle \operatorname {li} (x)=x\int _{0}^{1}{\frac {\mathrm {d} t}{\ln(x\,t)}}\ ,} wobei für x > 1 {\displaystyle x>1} t = 1 / x {\displaystyle t=1/x} x ≥ 0 , x ≠ 1 {\displaystyle x\geq 0,x\neq 1}
∫ 0 x li ( t ) d t = x li ( x ) − li ( x 2 ) . {\displaystyle \int _{0}^{x}\operatorname {li} (t)\,{\mathrm {d} t}=x\,\operatorname {li} (x)-\operatorname {li} (x^{2}).} Außerdem gilt für p > − 1 , p ≠ 0 {\displaystyle p>-1,p\not =0}
∫ 0 1 li ( t ) t p − 1 d t = − 1 p ln ( p + 1 ) , {\displaystyle \int _{0}^{1}\operatorname {li} (t)\,t^{p-1}\,\mathrm {d} t=-{\tfrac {1}{p}}\ln(p+1),} für p = 1 {\displaystyle p=1} ∫ 0 1 li ( t ) d t = − ln 2. {\displaystyle \textstyle \int _{0}^{1}\operatorname {li} (t)\,\mathrm {d} t=-\ln 2.} p = 0 {\displaystyle p=0} ∫ 0 1 li ( t ) t − 1 d t = − 1. {\displaystyle \textstyle \int _{0}^{1}\operatorname {li} (t)\,t^{-1}\,\mathrm {d} t=-1.}
Eine weitere Formel ist ∫ 0 1 li ( t − 1 ) t d t = ∫ 1 ∞ li ( t ) t − 3 d t = 0. {\displaystyle \textstyle \int _{0}^{1}\operatorname {li} (t^{-1})\,t\,\mathrm {d} t=\textstyle \int _{1}^{\infty }\operatorname {li} (t)\,t^{-3}\,\mathrm {d} t=0.}
Die Golomb-Dickman-Konstante λ = ∫ 0 1 e li ( x ) d x = 0,624 32 99885 43550 87099 … {\displaystyle \lambda =\textstyle \int _{0}^{1}\mathrm {e} ^{\operatorname {li} (x)}\mathrm {d} x=0{,}62432\;99885\;43550\;87099\ldots } A084945 in OEIS ) tritt in der Theorie zufälliger Permutationen bei der Abschätzung der Länge des längsten Zykels einer Permutation und in der Zahlentheorie bei der Abschätzung der Größe des größten Primfaktors einer Zahl auf.
Asymptotisches Verhalten Funktionsgraph von li ( x ) {\displaystyle \operatorname {li} (x)} 13 Für große x {\displaystyle x} li ( x ) {\displaystyle \operatorname {li} (x)}
li ( x ) = 0 ! x ln x + 1 ! x ln 2 x + 2 ! x ln 3 x + 3 ! x ln 4 x + ⋯ {\displaystyle \operatorname {li} (x)=0!\,{\frac {x}{\ln x}}+1!\,{\frac {x}{\ln ^{2}x}}+2!\,{\frac {x}{\ln ^{3}x}}+3!\,{\frac {x}{\ln ^{4}x}}+\dotsb } approximieren . Die Reihe ist eine asymptotische Entwicklung ; sie konvergiert nicht, sondern nähert sich dem wahren Wert an, um sich dann wieder zu entfernen. Die beste Approximation wird nach etwa ln x {\displaystyle \ln x} Fakultät .
Siehe auch Literatur Weblinks