Innenwinkel
Die Innenwinkel eines Polygons sind in der Geometrie die Winkel, die durch zwei benachbarte Polygonseiten eingeschlossen werden und im Inneren des Polygons liegen. Die Ecken des Polygons bilden dabei die Scheitelpunkte der Innenwinkel. Jedes -Eck besitzt genau Innenwinkel. In einem nicht-überschlagenen Polygon hängt die Innenwinkelsumme nur von der Anzahl der Ecken des Polygons ab. Ein Nebenwinkel eines Innenwinkels, der durch Verlängerung einer Polygonseite entsteht, wird Außenwinkel genannt.
Bezeichnungen
Werden die Ecken eines Polygons mit bezeichnet, so werden die Innenwinkel meist genannt. Die Ecke ist dabei der Scheitelpunkt des Winkels , die Ecke der Scheitelpunkt des Winkels und so weiter. Bei einem Dreieck wird die dem Winkel gegenüberliegende Seite mit bezeichnet, die dem Winkel gegenüberliegende Seite mit und so fort (siehe Abbildung).[1]
Spezialfälle
- Sind in einem Dreieck alle Innenwinkel kleiner als , heißt es spitzwinklig; misst einer der Innenwinkel genau , rechtwinklig; und ist einer der Innenwinkel größer als , stumpfwinklig. Bei einem gleichschenkligen Dreieck sind zwei der drei Innenwinkel gleich groß.
- Sind bei einem Viereck je zwei gegenüber liegende Innenwinkel gleich groß, liegt ein Parallelogramm vor; sind je zwei nebeneinander liegende Innenwinkel gleich groß, ein gleichschenkliges Trapez. Bei einem Sehnenviereck ergänzen sich je zwei gegenüberliegende Innenwinkel zu .
- Bei einem gleichwinkligen Polygon sind alle Innenwinkel gleich groß. Wichtige Beispiele für gleichwinklige Polygone sind die regelmäßigen Polygone, beispielsweise das gleichseitige Dreieck, das Quadrat oder das regelmäßige Fünfeck, bei denen auch alle Seiten gleich lang sind.
- In einem konvexen Polygon messen alle Innenwinkel höchstens . Bei einem nichtkonvexen Polygon gibt es demnach mindestens eine einspringende Ecke mit einem Innenwinkel von mehr als .
- Zwei Polygone sind nicht notwendigerweise zueinander ähnlich, wenn alle einander entsprechenden Innenwinkel übereinstimmen. Zum Beispiel sind Rechtecke mit verschiedenen Seitenverhältnissen nicht ähnlich zueinander.
Eigenschaften
Winkelsumme
Die Summe der Innenwinkel eines nicht überschlagenen -Ecks ergibt sich in der euklidischen Geometrie stets zu
- .
In einem Dreieck beträgt die Innenwinkelsumme daher immer , in einem Viereck immer und in einem Fünfeck immer . In einem gleichwinkligen (und damit speziell auch in einem regelmäßigen) Polygon mit Ecken ergeben sich damit alle Innenwinkel zu
- .
In einem gleichseitigen Dreieck messen daher alle Innenwinkel , in einem Quadrat und in einem regelmäßigen Fünfeck . Diese Aussagen gelten in nichteuklidischen Geometrien jedoch nicht mehr. In einer elliptischen Geometrie, beispielsweise auf einer Kugeloberfläche, ist die Innenwinkelsumme stets größer als in der euklidischen Geometrie, in einer hyperbolischen Geometrie, beispielsweise auf einer Sattelfläche, stets kleiner.
Winkelhalbierende
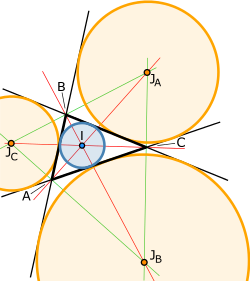
Die Winkelhalbierenden der Innenwinkel eines Tangentenvielecks, beispielsweise eines Dreiecks oder einer Raute, treffen sich im Inkreismittelpunkt des Vielecks.
In einem Dreieck teilt jede Innenwinkelhalbierende die gegenüberliegende Seite im Verhältnis der beiden anliegenden Seiten. Zudem schneidet sie die Winkelhalbierenden der beiden nicht anliegenden Außenwinkel im Mittelpunkt des Ankreises der gegenüberliegenden Seite.
Mathematische Sätze
Beziehungen zwischen den Innenwinkeln und den Seiten eines Dreiecks stellen unter anderem der Sinussatz, der Kosinussatz, der Tangenssatz, die Halbwinkelsätze und die mollweideschen Formeln her.
Nach dem Außenwinkelsatz ist jeder Außenwinkel eines Dreiecks gleich der Summe der beiden nichtanliegenden Innenwinkel. Nach dem Satz von Morley ist das Morley-Dreieck, welches durch Drittelung der drei Innenwinkel eines Dreiecks entsteht, stets gleichseitig.
In gleichwinkligen Polygonen gilt der Satz von Viviani, nach dem die Summe der Abstände von einem beliebigen Punkt im Inneren des Polygons zu den Polygonseiten unabhängig von der Position des Punkts ist.
Literatur
- Ilka Agricola, Thomas Friedrich: Elementargeometrie. Springer, 2010, ISBN 978-3-8348-9826-5.
- Arnfried Kemnitz: Mathematik zum Studienbeginn. Springer, 2014, ISBN 978-3-658-02081-1.
Einzelnachweise
- ↑ Arnfried Kemnitz: Mathematik zum Studienbeginn. Springer, 2014, S. 131–132.
Weblinks
Auf dieser Seite verwendete Medien
Autor/Urheber: User:J Hokkanen, Lizenz: CC BY-SA 3.0
Konkaves Fünfeck mit Innenwinkeln
Autor/Urheber: MartinThoma, Lizenz: CC BY 3.0
Bild eines Dreiecks, bei dem einige Winkel markiert sind. Es veranschaulicht, dass die Innenwinkel sich zu 180 aufsummieren. Die geleiche Farbe bei den Winkeln bedeutet, dass die Winkel den gleichen Wert haben.
Diagram to shown the construction of the incenter (blue, I), the incircle (blue), the excentres (orange, JA,JB,JC and the excircles (orange).