Der hyperbolisch lemniskatische Sinus oder sinus lemniscatus hyperbolicus (kurz sinlemnh oder slh) ist eine spezielle mathematische Funktion . Sie zählt zu den elliptischen Funktionen .
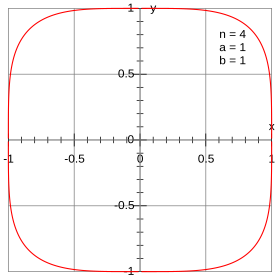
Definitionen Rot: Sinus lemniscatus hyperbolicus Definition über den Sinus lemniscatus und Kosinus lemniscatus:
s l h ( x ) = s l ( x / 2 ) ⋅ [ c l ( x / 2 ) 2 + 1 ] 2 ⋅ c l ( x / 2 ) {\displaystyle \mathrm {slh} \,(x)={\frac {\mathrm {sl} \,(x/{\sqrt {2}})\cdot [\mathrm {cl} \,(x/{\sqrt {2}})^{2}+1]}{{\sqrt {2}}\cdot \mathrm {cl} \,(x/{\sqrt {2}})}}} Definition über Jacobische elliptische Funktionen :
s l h ( x ) = sn ( x ; 1 / 2 ) cd ( x ; 1 / 2 ) {\displaystyle \mathrm {slh} \,(x)={\frac {\operatorname {sn} (x;1/{\sqrt {2}})}{\operatorname {cd} (x;1/{\sqrt {2}})}}} Definition über Thetafunktionen :
s l h ( x ) = ϑ 00 ( 1 2 2 π ϖ − 1 x ; e − π ) ϑ 10 ( 1 2 π − 1 2 2 π ϖ − 1 x ; e − π ) ϑ 10 ( 1 2 2 π ϖ − 1 x ; e − π ) ϑ 00 ( 1 2 π − 1 2 2 π ϖ − 1 x ; e − π ) {\displaystyle \mathrm {slh} \,(x)={\frac {\vartheta _{00}({\tfrac {1}{2}}{\sqrt {2}}\pi \varpi ^{-1}x;\operatorname {e} ^{-\pi })\vartheta _{10}({\tfrac {1}{2}}\pi -{\tfrac {1}{2}}{\sqrt {2}}\pi \varpi ^{-1}x;\operatorname {e} ^{-\pi })}{\vartheta _{10}({\tfrac {1}{2}}{\sqrt {2}}\pi \varpi ^{-1}x;\operatorname {e} ^{-\pi })\vartheta _{00}({\tfrac {1}{2}}\pi -{\tfrac {1}{2}}{\sqrt {2}}\pi \varpi ^{-1}x;\operatorname {e} ^{-\pi })}}} Definition über die Umkehrfunktion r = r ( s ) {\displaystyle r=r(s)} elliptischen Integrals :
s ( r ) = ∫ 0 r d ρ ρ 4 + 1 {\displaystyle s(r)=\int _{0}^{r}{\frac {\mathrm {d} \rho }{\sqrt {\rho ^{4}+1}}}} Dann gilt: r = s l h s {\displaystyle r=\mathrm {slh} \,s}
Dabei gelten folgende zwei Integrale:[ 1]
∫ 0 1 d ρ ρ 4 + 1 = ϖ 2 2 {\displaystyle \int _{0}^{1}{\frac {\mathrm {d} \rho }{\sqrt {\rho ^{4}+1}}}={\frac {\varpi }{2{\sqrt {2}}}}} ∫ 0 ∞ d ρ ρ 4 + 1 = ϖ 2 {\displaystyle \int _{0}^{\infty }{\frac {\mathrm {d} \rho }{\sqrt {\rho ^{4}+1}}}={\frac {\varpi }{\sqrt {2}}}} Durch Spiegelung an der senkrechten Achse beim x-Wert ϖ/sqrt(8) oder auch durch Kehrwertbildung entsteht der Kosinus lemniscatus hyperbolicus als Funktion:
c l h ( x ) = s l h ( 1 2 2 ϖ − x ) = 1 s l h ( x ) {\displaystyle \mathrm {clh} \,(x)=\mathrm {slh} \,({\tfrac {1}{2}}{\sqrt {2}}\varpi -x)={\frac {1}{\mathrm {slh} \,(x)}}} Jedoch wird die Umkehrfunktion des Sinus lemniscatus hyperbolicus Areasinus lemniscatus hyperbolicus oder Arcussinus lemniscatus hyperbolicus genannt.
Der erste Begriff bezieht sich hierbei auf die Flächenmaße der Superellipse und der zweite Begriff bezieht sich auf die Bogenmaße der Lemniskate.
s ( r ) = a s l h ( r ) {\displaystyle s(r)=\mathrm {aslh} (r)} Daher gelten auch folgende Identitäten:[ 2]
a s l h ( x ) = ∫ 0 1 x x 4 y 4 + 1 d y {\displaystyle \mathrm {aslh} (x)=\int _{0}^{1}{\frac {x}{\sqrt {x^{4}y^{4}+1}}}\mathrm {d} y} a s l h ( x ) = 2 arcsl [ x ( x 4 + 1 + 1 ) − 1 / 2 ] {\displaystyle \mathrm {aslh} (x)={\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}} a s l h ( x ) = 1 2 F [ 2 arctan ( x ) ; 1 2 2 ] {\displaystyle \mathrm {aslh} (x)={\tfrac {1}{2}}F[2\arctan(x);{\tfrac {1}{2}}{\sqrt {2}}]} a s l h ( x ) = F [ arcsin ( 1 2 2 x 2 + 2 2 x + 2 − 1 2 2 x 2 − 2 2 x + 2 ) ; 1 2 2 ] {\displaystyle \mathrm {aslh} (x)=F[\arcsin({\tfrac {1}{2}}{\sqrt {2x^{2}+2{\sqrt {2}}\,x+2}}-{\tfrac {1}{2}}{\sqrt {2x^{2}-2{\sqrt {2}}\,x+2}});{\tfrac {1}{2}}{\sqrt {2}}]} Die an der waagrechten Spiegelachse vom Ordinatenwert ϖ/sqrt(8) gespiegelte Funktion wird Areacosinus lemniscatus hyperbolicus genannt:
a c l h ( x ) = 1 2 2 ϖ − 2 arcsl [ x ( x 4 + 1 + 1 ) − 1 / 2 ] {\displaystyle \mathrm {aclh} (x)={\tfrac {1}{2}}{\sqrt {2}}\,\varpi -{\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}} a c l h ( x ) = 1 2 F [ 2 arccot ( x ) ; 1 2 2 ] {\displaystyle \mathrm {aclh} (x)={\tfrac {1}{2}}F[2\operatorname {arccot}(x);{\tfrac {1}{2}}{\sqrt {2}}]}
Lemniskate
In der Lemniskate von Bernoulli mit der kartesischen Relation (x² + y²)² = 2f²(x² − y²) kann der invertierte Sinus lemniscatus hyperbolicus immer als Verhältnis der lemniskatischen Kurvenlänge zur Brennweite f angegeben werden. Hierbei nimmt das vom Koordinatenursprungspunkt und somit Kurvenschnittpunkt S ausgehende Bogenmaß bis zu einem Punkt P mit folgender Parametrisierung immer den Wert des Produkts aus Brennweite f und invertiertem Sinus lemniscatus hyperbolicus vom Parameter t an:
P = ( f t t 2 + 1 + t 4 + 1 t 4 + 1 + 1 | f t t 4 + 1 − t 2 + 1 t 4 + 1 + 1 ) {\displaystyle P={\biggl (}{\frac {ft{\sqrt {t^{2}+1+{\sqrt {t^{4}+1}}}}}{{\sqrt {t^{4}+1}}+1}}{\bigg \vert }{\frac {ft{\sqrt {{\sqrt {t^{4}+1}}-t^{2}+1}}}{{\sqrt {t^{4}+1}}+1}}{\biggr )}} Die genannten Parameter für x und y erfüllen die kartesische Relation:
x = f t t 2 + 1 + t 4 + 1 t 4 + 1 + 1 {\displaystyle x={\frac {ft{\sqrt {t^{2}+1+{\sqrt {t^{4}+1}}}}}{{\sqrt {t^{4}+1}}+1}}} y = f t t 4 + 1 − t 2 + 1 t 4 + 1 + 1 {\displaystyle y={\frac {ft{\sqrt {{\sqrt {t^{4}+1}}-t^{2}+1}}}{{\sqrt {t^{4}+1}}+1}}} ( x 2 + y 2 ) 2 = 2 f 2 ( x 2 − y 2 ) {\displaystyle (x^{2}+y^{2})^{2}=2f^{2}(x^{2}-y^{2})}
Beweis der Parametrisierung Die lemniskatische Kurvenlänge vom Punkt S bis zum Punkt P wird im Folgenden mit L(t) bezeichnet:
L ( t ) = f a s l h ( t ) {\displaystyle L(t)=f\,\mathrm {aslh} (t)} Dies kann mit dem Integral vom Pythagoras der partiellen Ableitungen der Parametrisierungen gezeigt werden:
d d t L ( t ) = [ ( d d t f t t 2 + 1 + t 4 + 1 t 4 + 1 + 1 ) 2 + ( d d t f t t 4 + 1 − t 2 + 1 t 4 + 1 + 1 ) 2 ] 1 / 2 = {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}L(t)={\biggl [}{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {ft{\sqrt {t^{2}+1+{\sqrt {t^{4}+1}}}}}{{\sqrt {t^{4}+1}}+1}}{\biggr )}^{2}+{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {ft{\sqrt {{\sqrt {t^{4}+1}}-t^{2}+1}}}{{\sqrt {t^{4}+1}}+1}}{\biggr )}^{2}{\biggr ]}^{1/2}=} = { [ f ( 2 t 2 + 1 + t 4 + 1 ) ( t 4 + 1 + t 4 + 1 ) t 2 + 1 + t 4 + 1 ] 2 + [ f ( t 4 + 1 − 2 t 2 + 1 ) ( t 4 + 1 + t 4 + 1 ) t 4 + 1 − t 2 + 1 ] 2 } 1 / 2 = {\displaystyle ={\biggl \{}{\biggl [}{\frac {f(2t^{2}+1+{\sqrt {t^{4}+1}})}{(t^{4}+1+{\sqrt {t^{4}+1}}){\sqrt {t^{2}+1+{\sqrt {t^{4}+1}}}}}}{\biggr ]}^{2}+{\biggl [}{\frac {f({\sqrt {t^{4}+1}}-2t^{2}+1)}{(t^{4}+1+{\sqrt {t^{4}+1}}){\sqrt {{\sqrt {t^{4}+1}}-t^{2}+1}}}}{\biggr ]}^{2}{\biggr \}}^{1/2}=} = [ f 2 ( t 4 + 1 − t 2 + 1 ) ( 2 t 2 + 1 + t 4 + 1 ) 2 + f 2 ( t 2 + 1 + t 4 + 1 ) ( t 4 + 1 − 2 t 2 + 1 ) 2 ( t 2 + 1 + t 4 + 1 ) ( t 4 + 1 − t 2 + 1 ) ( t 4 + 1 + t 4 + 1 ) 2 ] 1 / 2 = {\displaystyle ={\biggl [}{\frac {f^{2}({\sqrt {t^{4}+1}}-t^{2}+1)(2t^{2}+1+{\sqrt {t^{4}+1}})^{2}+f^{2}(t^{2}+1+{\sqrt {t^{4}+1}})({\sqrt {t^{4}+1}}-2t^{2}+1)^{2}}{(t^{2}+1+{\sqrt {t^{4}+1}})({\sqrt {t^{4}+1}}-t^{2}+1)(t^{4}+1+{\sqrt {t^{4}+1}})^{2}}}{\biggr ]}^{1/2}=} = f ( t 4 + 1 − t 2 + 1 ) ( 2 t 2 + 1 + t 4 + 1 ) 2 + ( t 2 + 1 + t 4 + 1 ) ( t 4 + 1 − 2 t 2 + 1 ) 2 ( t 4 + 1 + t 4 + 1 ) 2 ( t 4 + 1 + 1 ) = {\displaystyle ={\frac {f{\sqrt {({\sqrt {t^{4}+1}}-t^{2}+1)(2t^{2}+1+{\sqrt {t^{4}+1}})^{2}+(t^{2}+1+{\sqrt {t^{4}+1}})({\sqrt {t^{4}+1}}-2t^{2}+1)^{2}}}}{(t^{4}+1+{\sqrt {t^{4}+1}}){\sqrt {2({\sqrt {t^{4}+1}}+1)}}}}=} = 2 f ( t 4 + 1 + 1 ) 3 / 2 ( t 4 + 1 + t 4 + 1 ) 2 ( t 4 + 1 + 1 ) = f t 4 + 1 {\displaystyle ={\frac {{\sqrt {2}}\,f({\sqrt {t^{4}+1}}+1)^{3/2}}{(t^{4}+1+{\sqrt {t^{4}+1}}){\sqrt {2({\sqrt {t^{4}+1}}+1)}}}}={\frac {f}{\sqrt {t^{4}+1}}}} Die Ursprungsstammfunktion beschreibt das Bogenmaß von S nach P:
L ( t ) = ∫ 0 1 { t [ d d v L ( v ) ( v = t u ) ] } d u = ∫ 0 1 f t t 4 u 4 + 1 d u = f a s l h ( t ) {\displaystyle L(t)=\int _{0}^{1}{\biggl \{}t{\biggl [}{\frac {\mathrm {d} }{\mathrm {d} v}}L(v)(v=tu){\biggr ]}{\biggr \}}\mathrm {d} u=\int _{0}^{1}{\frac {ft}{\sqrt {t^{4}u^{4}+1}}}\mathrm {d} u=f\,\mathrm {aslh} (t)}
Superellipse Superellipse mit der Relation x 4 + y 4 = 1 {\displaystyle x^{4}+y^{4}=1} In einer Superellipse der Gleichung x⁴ + y⁴ = 1 ist der Sinus lemniscatus hyperbolicus analog zum Tangens in einem Kreis definiert. Wenn der Koordinatenursprung und ein Punkt auf dem Bogen des Kreises durch eine Strecke miteinander verbunden sind, dann ordnet der Sinus lemniscatus hyperbolicus das Doppelte der zwischen dieser Strecke und der x-Achse eingeschlossenen Fläche A dem Quotienten der vertikalen Koordinate des Bogenpunktes dividiert durch seine horizontale Koordinate zu. Dies wird im nun Folgenden demonstriert.
Differentialgleichungssystem mit zwei Unbekannten Die horizontalen und vertikalen Koordinaten dieser Superellipse sind in Abhängigkeit vom Doppelten der eingeschlossenen Fläche w = 2A müssen somit folgende Bedingungen erfüllen:
x ( w ) 4 + y ( w ) 4 = 1 {\displaystyle x(w)^{4}+y(w)^{4}=1} d d w x ( w ) = − y ( w ) 3 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} w}}x(w)=-y(w)^{3}} d d w y ( w ) = x ( w ) 3 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} w}}y(w)=x(w)^{3}} x ( w = 0 ) = 1 {\displaystyle x(w=0)=1} y ( w = 0 ) = 0 {\displaystyle y(w=0)=0} Die Lösungen dieses Gleichungssystems lauten wie folgt:
x ( w ) = cl ( 1 2 2 w ) [ sl ( 1 2 2 w ) 2 + 1 ] 1 / 2 [ sl ( 1 2 2 w ) 2 + cl ( 1 2 2 w ) 2 ] − 1 / 2 {\displaystyle x(w)=\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}} y ( w ) = sl ( 1 2 2 w ) [ cl ( 1 2 2 w ) 2 + 1 ] 1 / 2 [ sl ( 1 2 2 w ) 2 + cl ( 1 2 2 w ) 2 ] − 1 / 2 {\displaystyle y(w)=\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}} Für den Quotienten gilt somit Folgendes:
y ( w ) x ( w ) = sl ( 1 2 2 w ) [ cl ( 1 2 2 w ) 2 + 1 ] 1 / 2 cl ( 1 2 2 w ) [ sl ( 1 2 2 w ) 2 + 1 ] 1 / 2 = slh ( w ) {\displaystyle {\frac {y(w)}{x(w)}}={\frac {\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}{\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}}=\operatorname {slh} (w)} Die Funktionen x(w) und y(w) werden Kotangens lemniscatus hyperbolicus und Tangens lemniscatus hyperbolicus genannt.
x ( w ) = ctlh ( w ) {\displaystyle x(w)={\text{ctlh}}(w)} y ( w ) = tlh ( w ) {\displaystyle y(w)={\text{tlh}}(w)} Aus der Skizze ist auch die Tatsache entnehmbar, dass die Ableitung der Funktion Areasinus lemniscatus hyperbolicus gleich dem Kehrwert der Quadratwurzel aus dem Nachfolger von der vierten Potenzfunktion ist.
Erster Beweis: Vergleich mit der Ableitung des Arkustangens Bei gegebener Fermatscher Superellipse mit der Relation x 4 + y 4 = 1 {\displaystyle x^{4}+y^{4}=1} Auf der rechts abgebildeten Skizze befindet sich eine schwarze Diagonale. Die Länge derjenigen Strecke, welche vom Schnittpunkt dieser schwarzen Diagonalen mit der roten senkrechten Achse bis hin zum Punkt (1|0) senkrecht verläuft, soll s genannt werden. Und die Länge vom Abschnitt der schwarzen Diagonalen vom Koordinatenursprungspunkt bis zum Schnittpunkt dieser Diagonale mit der cyanen Kurvenlinie der Superellipse hat in Abhängigkeit vom slh-Wert folgenden Wert:
D ( s ) = ( 1 s 4 + 1 4 ) 2 + ( s s 4 + 1 4 ) 2 = s 2 + 1 s 4 + 1 4 {\displaystyle D(s)={\sqrt {{\biggl (}{\frac {1}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}+{\biggl (}{\frac {s}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}}}={\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}} Dieser Zusammenhang wird durch den Satz des Pythagoras beschrieben.
Ein analoger Einheitskreis ergibt bei der beschriebenen Flächenzuordnung den kreistrigonometrischen Arkustangens.
Für diesen gilt folgende Ableitung:
d d s arctan ( s ) = 1 s 2 + 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s)={\frac {1}{s^{2}+1}}} Für die Ermittlung der Ableitung des Areasinus lemniscatus hyperbolicus wird im Folgenden der Vergleich der infinitesimal kleinen Dreiecksflächen für die gleiche Diagonale bei der Superellipse und beim Einheitskreis aufgestellt. Denn die Aufsummierung der infinitesimal kleinen Dreiecksflächen beschreibt die Flächenmaße. Bei der Superellipse im Bild ist die Hälfte des betroffenen Flächenmaßes grün abgebildet. Wegen des quadratischen Verhältnisses der Flächen zu den Längen bei den Dreiecken mit gleichem infinitesimal kleinem Winkel am Koordinatenursprungspunkt gilt folgende Formel:
d d s aslh ( s ) = [ d d s arctan ( s ) ] D ( s ) 2 = 1 s 2 + 1 D ( s ) 2 = 1 s 2 + 1 ( s 2 + 1 s 4 + 1 4 ) 2 = 1 s 4 + 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}{\text{aslh}}(s)={\biggl [}{\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s){\biggr ]}D(s)^{2}={\frac {1}{s^{2}+1}}D(s)^{2}={\frac {1}{s^{2}+1}}{\biggl (}{\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}={\frac {1}{\sqrt {s^{4}+1}}}}
Der Areatangens lemniscatus hyperbolicus ordnet im gezeigten Bild die Höhe des Schnittpunkts von Diagonale und Kurvenlinie dem Doppelten der grünen Fläche zu. Die grüne Fläche selbst entsteht als Differenz Integral der Superellipsenfunktion von Null bis zum betroffenen Höhenwert minus Fläche des anliegenden Dreiecks:
atlh ( v ) = 2 ( ∫ 0 v 1 − w 4 4 d w ) − v 1 − v 4 4 {\displaystyle {\text{atlh}}(v)=2{\biggl (}\int _{0}^{v}{\sqrt[{4}]{1-w^{4}}}\mathrm {d} w{\biggr )}-v{\sqrt[{4}]{1-v^{4}}}} d d v atlh ( v ) = 2 1 − v 4 4 − ( d d v v 1 − v 4 4 ) = 1 ( 1 − v 4 ) 3 / 4 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} v}}{\text{atlh}}(v)=2{\sqrt[{4}]{1-v^{4}}}-{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} v}}v{\sqrt[{4}]{1-v^{4}}}{\biggr )}={\frac {1}{(1-v^{4})^{3/4}}}} Es gilt folgende Transformation:
aslh ( x ) = atlh ( x x 4 + 1 4 ) {\displaystyle {\text{aslh}}(x)={\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}} Und somit gilt nach der Kettenregel diese Ableitung:
d d x aslh ( x ) = d d x atlh ( x x 4 + 1 4 ) = ( d d x x x 4 + 1 4 ) [ 1 − ( x x 4 + 1 4 ) 4 ] − 3 / 4 = {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{aslh}}(x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}={\biggl (}{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}=} = 1 ( x 4 + 1 ) 5 / 4 [ 1 − ( x x 4 + 1 4 ) 4 ] − 3 / 4 = 1 ( x 4 + 1 ) 5 / 4 ( 1 x 4 + 1 ) − 3 / 4 = 1 x 4 + 1 {\displaystyle ={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl (}{\frac {1}{x^{4}+1}}{\biggr )}^{-3/4}={\frac {1}{\sqrt {x^{4}+1}}}}
Hyperbolisch lemniskatischer Tangens und Kotangens
Die Funktionen tlh und ctlh erfüllen diese in der genannten Differentialgleichung beschriebenen Identitäten:
tlh ( x ) = sl ( 1 2 2 x ) [ cl ( 1 2 2 x ) 2 + 1 sl ( 1 2 2 x ) 2 + cl ( 1 2 2 x ) 2 ] 1 / 2 {\displaystyle {\text{tlh}}(x)=\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}x){\biggl [}{\frac {\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}+1}{\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}}}{\biggr ]}^{1/2}} ctlh ( x ) = cl ( 1 2 2 x ) [ sl ( 1 2 2 x ) 2 + 1 sl ( 1 2 2 x ) 2 + cl ( 1 2 2 x ) 2 ] 1 / 2 {\displaystyle {\text{ctlh}}(x)=\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}x){\biggl [}{\frac {\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}+1}{\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}}}{\biggr ]}^{1/2}} Die Funktionsbezeichnung sl steht für den Sinus lemniscatus und die Bezeichnung cl steht für den Kosinus lemniscatus. Außerdem sind jene Beziehungen zu den Jacobischen elliptischen Funktionen gültig:
tlh ( x ) = sn ( x ; 1 2 2 ) cd ( x ; 1 2 2 ) 4 + sn ( x ; 1 2 2 ) 4 4 {\displaystyle {\text{tlh}}(x)={\frac {{\text{sn}}(x;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(x;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(x;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}} ctlh ( x ) = cd ( x ; 1 2 2 ) cd ( x ; 1 2 2 ) 4 + sn ( x ; 1 2 2 ) 4 4 {\displaystyle {\text{ctlh}}(x)={\frac {{\text{cd}}(x;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(x;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(x;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}} Jene Formeln zeigen die Tatsache, dass der Quotient der oberen Funktion dividiert durch die untere Funktion den Sinus lemniscatus hyperbolicus ergibt. Und sie zeigen zugleich, dass die Summe der vierten Potenzen dieser beiden Funktionen den konstanten Wert Eins ergibt. Es gilt für die Ableitungen:
d d x tlh ( x ) = ctlh ( x ) 3 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{tlh}}(x)={\text{ctlh}}(x)^{3}} d d x ctlh ( x ) = − tlh ( x ) 3 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{ctlh}}(x)=-{\text{tlh}}(x)^{3}}
Analog zur Ermittlung des uneigentlichen Integrals bei der Gaußschen Glockenkurvenfunktion kann zur Berechnung des Integrals von 0 bis ∞ bei der Funktion f(x) = exp(−x⁴) die Koordinatentransformation von einem allgemeinen Zylinder verwendet werden. Im Folgenden werden die Beweise von beiden Integralen parallel aufgeführt.
Dies ist die Zylinderkoordinatentransformation bei der Gaußschen Glockenkurvenfunktion:
[ ∫ 0 ∞ exp ( − x 2 ) d x ] 2 = ∫ 0 ∞ ∫ 0 ∞ exp ( − x 2 − y 2 ) d x d y = {\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-x^{2}-y^{2})\,\mathrm {d} x\,\mathrm {d} y=} = ∫ 0 π / 2 ∫ 0 ∞ det [ ∂ / ∂ r r cos ( ϕ ) ∂ / ∂ ϕ r cos ( ϕ ) ∂ / ∂ r r sin ( ϕ ) ∂ / ∂ ϕ r sin ( ϕ ) ] exp { − [ r cos ( ϕ ) ] 2 − [ r sin ( ϕ ) ] 2 } d r d ϕ = {\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\cos(\phi )&\partial /\partial \phi \,\,r\cos(\phi )\\\partial /\partial r\,\,r\sin(\phi )&\partial /\partial \phi \,\,r\sin(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\cos(\phi ){\bigr ]}^{2}-{\bigl [}r\sin(\phi ){\bigr ]}^{2}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =} = ∫ 0 π / 2 ∫ 0 ∞ r exp ( − r 2 ) d r d ϕ = ∫ 0 π / 2 1 2 d ϕ = π 4 {\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }r\exp(-r^{2})\,\mathrm {d} r\,\mathrm {d} \phi =\int _{0}^{\pi /2}{\frac {1}{2}}\,\mathrm {d} \phi ={\frac {\pi }{4}}} Und das ist die analoge Koordinatentransformation für den lemniskatischen Fall:
[ ∫ 0 ∞ exp ( − x 4 ) d x ] 2 = ∫ 0 ∞ ∫ 0 ∞ exp ( − x 4 − y 4 ) d x d y = {\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{4})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-x^{4}-y^{4})\,\mathrm {d} x\,\mathrm {d} y=} = ∫ 0 ϖ / 2 ∫ 0 ∞ det [ ∂ / ∂ r r ctlh ( ϕ ) ∂ / ∂ ϕ r ctlh ( ϕ ) ∂ / ∂ r r tlh ( ϕ ) ∂ / ∂ ϕ r tlh ( ϕ ) ] exp { − [ r ctlh ( ϕ ) ] 4 − [ r tlh ( ϕ ) ] 4 } d r d ϕ = {\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\,{\text{ctlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{ctlh}}(\phi )\\\partial /\partial r\,\,r\,{\text{tlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{tlh}}(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\,{\text{ctlh}}(\phi ){\bigr ]}^{4}-{\bigl [}r\,{\text{tlh}}(\phi ){\bigr ]}^{4}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =} = ∫ 0 ϖ / 2 ∫ 0 ∞ r exp ( − r 4 ) d r d ϕ = ∫ 0 ϖ / 2 π 4 d ϕ = ϖ π 4 2 {\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }r\exp(-r^{4})\,\mathrm {d} r\,\mathrm {d} \phi =\int _{0}^{\varpi /{\sqrt {2}}}{\frac {\sqrt {\pi }}{4}}\,\mathrm {d} \phi ={\frac {\varpi {\sqrt {\pi }}}{4{\sqrt {2}}}}} In beiden Fällen wird die Determinante der Jacobi-Matrix an die jeweils ursprüngliche Funktion im Integrationsbereich anmultipliziert.
Die dadurch entstehenden neuen Funktionen im Integrationsbereich werden im Anschluss nach den neuen Parametern integriert.
Additionstheoreme und Kombinationstheoreme
Additionstheoreme Folgende algebraische Beziehung gilt für den Sinus lemniscatus hyperbolicus:
s l h ( x ) s l h ( ϖ / 2 − x ) = 1 {\displaystyle \mathrm {slh} (x)\,\mathrm {slh} (\varpi /{\sqrt {2}}-x)=1} für 0 < x < ϖ / 2 {\displaystyle 0<x<\varpi /{\sqrt {2}}}
Der Sinus lemniscatus hyperbolicus hat folgendes Additionstheorem:
s l h ( a + b ) = s l h ( a ) 1 + s l h ( b ) 4 + s l h ( b ) 1 + s l h ( a ) 4 1 − s l h ( a ) 2 s l h ( b ) 2 {\displaystyle \mathrm {slh} (a+b)={\frac {\mathrm {slh} (a){\sqrt {1+\mathrm {slh} (b)^{4}}}+\mathrm {slh} (b){\sqrt {1+\mathrm {slh} (a)^{4}}}}{1-\mathrm {slh} (a)^{2}\mathrm {slh} (b)^{2}}}} Und für den Kosinus lemniscatus hyperbolicus gilt:
c l h ( a + b ) = c l h ( a ) 2 c l h ( b ) 2 − 1 c l h ( a ) 1 + c l h ( b ) 4 + c l h ( b ) 1 + c l h ( a ) 4 {\displaystyle \mathrm {clh} (a+b)={\frac {\mathrm {clh} (a)^{2}\mathrm {clh} (b)^{2}-1}{\mathrm {clh} (a){\sqrt {1+\mathrm {clh} (b)^{4}}}+\mathrm {clh} (b){\sqrt {1+\mathrm {clh} (a)^{4}}}}}} Für die Verdopplung gilt folgende Formel:
s l h ( 2 x ) = 2 s l h ( x ) 1 + s l h ( x ) 4 1 − s l h ( x ) 4 {\displaystyle \mathrm {slh} (2x)={\frac {2\,\mathrm {slh} (x){\sqrt {1+\mathrm {slh} (x)^{4}}}}{1-\mathrm {slh} (x)^{4}}}} Für die Verdreifachung gilt Folgendes:
s l h ( 3 x ) = 3 s l h ( x ) + 6 s l h ( x ) 5 − s l h ( x ) 9 1 − 6 s l h ( x ) 4 − 3 s l h ( x ) 8 {\displaystyle \mathrm {slh} (3x)={\frac {3\,\mathrm {slh} (x)+6\,\mathrm {slh} (x)^{5}-\mathrm {slh} (x)^{9}}{1-6\,\mathrm {slh} (x)^{4}-3\,\mathrm {slh} (x)^{8}}}} Aus dem Additionstheorem des Sinus lemniscatus hyperbolicus folgen diese weiteren Theoreme:
tlh [ aslh ( v ) + aslh ( w ) ] = v 1 + w 4 + w 1 + v 4 ( 1 + v 2 w 2 ) ( 1 + v 4 ) ( 1 + w 4 ) + 2 v w ( v 2 + w 2 ) {\displaystyle {\text{tlh}}[{\text{aslh}}(v)+{\text{aslh}}(w)]={\frac {v{\sqrt {1+w^{4}}}+w{\sqrt {1+v^{4}}}}{\sqrt {(1+v^{2}w^{2}){\sqrt {(1+v^{4})(1+w^{4})}}+2vw(v^{2}+w^{2})}}}} ctlh [ aslh ( v ) + aslh ( w ) ] = 1 − v 2 w 2 ( 1 + v 2 w 2 ) ( 1 + v 4 ) ( 1 + w 4 ) + 2 v w ( v 2 + w 2 ) {\displaystyle {\text{ctlh}}[{\text{aslh}}(v)+{\text{aslh}}(w)]={\frac {1-v^{2}w^{2}}{\sqrt {(1+v^{2}w^{2}){\sqrt {(1+v^{4})(1+w^{4})}}+2vw(v^{2}+w^{2})}}}} Und für den lemniskatischen Sinus und den lemniskatischen Kosinus gilt:
sl [ 2 aslh ( v ) + 2 aslh ( w ) ] = 2 ( v 1 + w 4 + w 1 + v 4 ) ( 1 − v 2 w 2 ) ( 1 + v 2 w 2 ) ( 1 + v 4 ) ( 1 + w 4 ) + 2 v w ( v 2 + w 2 ) {\displaystyle {\text{sl}}[{\sqrt {2}}\,{\text{aslh}}(v)+{\sqrt {2}}\,{\text{aslh}}(w)]={\frac {{\sqrt {2}}\,(v{\sqrt {1+w^{4}}}+w{\sqrt {1+v^{4}}})(1-v^{2}w^{2})}{(1+v^{2}w^{2}){\sqrt {(1+v^{4})(1+w^{4})}}+2vw(v^{2}+w^{2})}}} cl [ 2 aslh ( v ) + 2 aslh ( w ) ] = ( 1 − v 2 w 2 ) 2 − ( v 1 + w 4 + w 1 + v 4 ) 2 ( 1 − v 2 w 2 ) 2 + ( v 1 + w 4 + w 1 + v 4 ) 2 {\displaystyle {\text{cl}}[{\sqrt {2}}\,{\text{aslh}}(v)+{\sqrt {2}}\,{\text{aslh}}(w)]={\frac {(1-v^{2}w^{2})^{2}-(v{\sqrt {1+w^{4}}}+w{\sqrt {1+v^{4}}})^{2}}{(1-v^{2}w^{2})^{2}+(v{\sqrt {1+w^{4}}}+w{\sqrt {1+v^{4}}})^{2}}}} Diese vier Formeln sind für alle reellen Werte v und w gültig.
Denn es gilt:
sl ( 2 x ) = 2 tlh ( x ) ctlh ( x ) {\displaystyle {\text{sl}}({\sqrt {2}}\,x)={\sqrt {2}}\,{\text{tlh}}(x){\text{ctlh}}(x)} cl ( 2 x ) = ctlh ( x ) 2 − tlh ( x ) 2 ctlh ( x ) 2 + tlh ( x ) 2 {\displaystyle {\text{cl}}({\sqrt {2}}\,x)={\frac {{\text{ctlh}}(x)^{2}-{\text{tlh}}(x)^{2}}{{\text{ctlh}}(x)^{2}+{\text{tlh}}(x)^{2}}}}
Kombinationstheoreme und Halbierungstheoreme In Kombination mit dem Areasinus lemniscatus hyperbolicus können folgende Identitäten aufgestellt werden:
tlh [ aslh ( x ) ] = ctlh [ aclh ( x ) ] = x x 4 + 1 4 {\displaystyle {\text{tlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{ctlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {x}{\sqrt[{4}]{x^{4}+1}}}} ctlh [ aslh ( x ) ] = tlh [ aclh ( x ) ] = 1 x 4 + 1 4 {\displaystyle {\text{ctlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{tlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {1}{\sqrt[{4}]{x^{4}+1}}}} Das Quadrat vom Tangens lemniscatus hyperbolicus ist das Pythagoräische Gegenstück zum Quadrat des Kotangens lemniscatus hyperbolicus.
Denn die vierten Potenzen von tlh und ctlh ergeben addiert konstant den Wert Eins.
Das Halbierungstheorem des Sinus lemniscatus hyperbolicus lautet so:
slh [ 1 2 aslh ( x ) ] = 2 x x 2 + 1 + x 4 + 1 + x 4 + 1 − x 2 + 1 {\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aslh}}(x){\bigr ]}={\frac {{\sqrt {2}}x}{{\sqrt {x^{2}+1+{\sqrt {x^{4}+1}}}}+{\sqrt {{\sqrt {x^{4}+1}}-x^{2}+1}}}}} Diese Formel kann als Kombination folgender zweier Formeln zum Vorschein gebracht werden:
a s l h ( x ) = 2 arcsl [ x ( x 4 + 1 + 1 ) − 1 / 2 ] {\displaystyle \mathrm {aslh} (x)={\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}} arcsl ( x ) = 2 aslh ( 2 x 1 + x 2 + 1 − x 2 ) {\displaystyle {\text{arcsl}}(x)={\sqrt {2}}\,{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}} Außerdem sind folgende Formeln für alle reellen Werte x ∈ R {\displaystyle x\in \mathbb {R} }
slh [ 1 2 aclh ( x ) ] = x 4 + 1 + x 2 − 2 x x 4 + 1 + x 2 = ( x 4 + 1 − x 2 + 1 ) − 1 / 2 ( x 4 + 1 + 1 − x ) {\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}-{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}} clh [ 1 2 aclh ( x ) ] = x 4 + 1 + x 2 + 2 x x 4 + 1 + x 2 = ( x 4 + 1 − x 2 + 1 ) − 1 / 2 ( x 4 + 1 + 1 + x ) {\displaystyle {\text{clh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}+{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}} Aus den zuletzt genannten Formel folgen diese Identitäten:
tlh [ 1 2 aclh ( x ) ] 2 = 1 2 2 − 2 2 x x 4 + 1 − x 2 = ( 2 x 2 + 2 + 2 x 4 + 1 ) − 1 / 2 ( x 4 + 1 + 1 − x ) {\displaystyle {\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2-2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}} ctlh [ 1 2 aclh ( x ) ] 2 = 1 2 2 + 2 2 x x 4 + 1 − x 2 = ( 2 x 2 + 2 + 2 x 4 + 1 ) − 1 / 2 ( x 4 + 1 + 1 + x ) {\displaystyle {\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2+2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}} Eng verwandt sind folgende Formeln für den lemniskatischen Sinus und lemniskatischen Cosinus:
sl [ 1 2 2 aclh ( x ) ] = cl [ 1 2 2 aslh ( x ) ] = x 4 + 1 − x 2 {\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}} sl [ 1 2 2 aslh ( x ) ] = cl [ 1 2 2 aclh ( x ) ] = x ( x 4 + 1 + 1 ) − 1 / 2 {\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]=x{\bigl (}{\sqrt {x^{4}+1}}+1{\bigr )}^{-1/2}}
Drittelungstheoreme Für die Drittelung des Flächenmaßes beziehungsweise Bogenmaßes beim Sinus lemniscatus hyperbolicus gelten für alle reellen Werte x ∈ R {\displaystyle x\in \mathbb {R} }
108 4 tan { 1 2 am [ 1 3 12 4 ( 3 + 1 ) aslh ( x ) ; λ ∗ ( 1 9 ) ] } − ( 3 + 1 ) tan { 1 2 am [ 1 3 12 4 ( 3 + 1 ) aslh ( x ) ; λ ∗ ( 1 9 ) ] } 3 3 + 1 − 108 4 tan { 1 2 am [ 1 3 12 4 ( 3 + 1 ) aslh ( x ) ; λ ∗ ( 1 9 ) ] } 2 = x {\displaystyle {\frac {{\sqrt[{4}]{108}}\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}({\tfrac {1}{9}})]\}-({\sqrt {3}}+1)\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}({\tfrac {1}{9}})]\}^{3}}{{\sqrt {3}}+1-{\sqrt[{4}]{108}}\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}({\tfrac {1}{9}})]\}^{2}}}=x} 3 4 ( 3 + 1 ) slh [ 1 3 aslh ( x ) ] + 2 slh [ 1 3 aslh ( x ) ] 3 2 + 3 4 ( 3 + 1 ) slh [ 1 3 aslh ( x ) ] 2 = tan { 1 2 am [ 1 3 12 4 ( 3 + 1 ) aslh ( x ) ; λ ∗ ( 1 9 ) ] } {\displaystyle {\frac {{\sqrt[{4}]{3}}({\sqrt {3}}+1)\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]+{\sqrt {2}}\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]^{3}}{{\sqrt {2}}+{\sqrt[{4}]{3}}({\sqrt {3}}+1)\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]^{2}}}=\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}({\tfrac {1}{9}})]\}} 108 4 tan { 1 2 am [ 1 3 12 4 ( 3 + 1 ) aslh ( x ) ; λ ∗ ( 9 ) ] } + ( 3 + 1 ) tan { 1 2 am [ 1 3 12 4 ( 3 + 1 ) aslh ( x ) ; λ ∗ ( 9 ) ] } 3 3 + 1 + 108 4 tan { 1 2 am [ 1 3 12 4 ( 3 + 1 ) aslh ( x ) ; λ ∗ ( 9 ) ] } 2 = x {\displaystyle {\frac {{\sqrt[{4}]{108}}\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}(9)]\}+({\sqrt {3}}+1)\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}(9)]\}^{3}}{{\sqrt {3}}+1+{\sqrt[{4}]{108}}\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}(9)]\}^{2}}}=x} 3 4 ( 3 + 1 ) slh [ 1 3 aslh ( x ) ] − 2 slh [ 1 3 aslh ( x ) ] 3 2 − 3 4 ( 3 + 1 ) slh [ 1 3 aslh ( x ) ] 2 = tan { 1 2 am [ 1 3 12 4 ( 3 + 1 ) aslh ( x ) ; λ ∗ ( 9 ) ] } {\displaystyle {\frac {{\sqrt[{4}]{3}}({\sqrt {3}}+1)\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]-{\sqrt {2}}\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]^{3}}{{\sqrt {2}}-{\sqrt[{4}]{3}}({\sqrt {3}}+1)\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]^{2}}}=\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}(9)]\}} Mit der Abkürzung am wird die Jacobische Amplitudenfunktion zum Ausdruck gebracht. Wichtiger Rechenhinweis:
λ ∗ ( 1 9 ) = 1 2 ( 3 − 1 ) ( 2 + 3 4 ) {\displaystyle \lambda ^{*}({\tfrac {1}{9}})={\tfrac {1}{2}}({\sqrt {3}}-1)({\sqrt {2}}+{\sqrt[{4}]{3}})} λ ∗ ( 9 ) = 1 2 ( 3 − 1 ) ( 2 − 3 4 ) {\displaystyle \lambda ^{*}(9)={\tfrac {1}{2}}({\sqrt {3}}-1)({\sqrt {2}}-{\sqrt[{4}]{3}})} Somit beinhaltet das Drittelungstheorem des Sinus lemniscatus hyperbolicus das Auflösen eines trikubischen Gleichungssystems.
Anwendung bei elliptischen Funktionen
Elliptische Lambdafunktion Diese beiden zuletzt genannten Ausdrücke haben in der Welt der elliptischen Funktionen eine hohe Bedeutung.
Denn einige elliptische Lambda-Stern-Funktionswerte ungerader Zahlen können so vereinfacht ausgedrückt werden:
λ ∗ ( 5 ) = tlh [ 1 2 aclh ( 2 ) ] 2 {\displaystyle \lambda ^{*}(5)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\sqrt {2}})]^{2}} λ ∗ ( 13 ) = tlh [ 1 2 aclh ( 3 2 ) ] 2 {\displaystyle \lambda ^{*}(13)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(3{\sqrt {2}})]^{2}} λ ∗ ( 21 ) = tlh [ 1 2 aclh ( 2 6 + 3 2 ) ] 2 {\displaystyle \lambda ^{*}(21)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(2{\sqrt {6}}+3{\sqrt {2}})]^{2}} λ ∗ ( 29 ) = tlh [ 1 2 aclh ( 13 3 2 + 2 3 412 2 + 12 174 3 + 2 3 412 2 − 12 174 3 ) ] 2 {\displaystyle \lambda ^{*}(29)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {13}{3}}{\sqrt {2}}+{\tfrac {2}{3}}{\sqrt[{3}]{412{\sqrt {2}}+12{\sqrt {174}}}}+{\tfrac {2}{3}}{\sqrt[{3}]{412{\sqrt {2}}-12{\sqrt {174}}}})]^{2}} λ ∗ ( 37 ) = tlh [ 1 2 aclh ( 21 2 ) ] 2 {\displaystyle \lambda ^{*}(37)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(21{\sqrt {2}})]^{2}} λ ∗ ( 45 ) = tlh [ 1 2 aclh ( 10 6 + 17 2 ) ] 2 {\displaystyle \lambda ^{*}(45)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(10{\sqrt {6}}+17{\sqrt {2}})]^{2}} λ ∗ ( 53 ) = tlh [ 1 2 aclh ( 55 3 2 + 2 3 37708 2 + 300 318 3 + 2 3 37708 2 − 300 318 3 ) ] 2 {\displaystyle \lambda ^{*}(53)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {55}{3}}{\sqrt {2}}+{\tfrac {2}{3}}{\sqrt[{3}]{37708{\sqrt {2}}+300{\sqrt {318}}}}+{\tfrac {2}{3}}{\sqrt[{3}]{37708{\sqrt {2}}-300{\sqrt {318}}}})]^{2}} λ ∗ ( 61 ) = tlh [ 1 2 aclh ( 27 2 + 2 5076 2 + 12 366 3 + 2 5076 2 − 12 366 3 ) ] 2 {\displaystyle \lambda ^{*}(61)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(27{\sqrt {2}}+2{\sqrt[{3}]{5076{\sqrt {2}}+12{\sqrt {366}}}}+2{\sqrt[{3}]{5076{\sqrt {2}}-12{\sqrt {366}}}})]^{2}} λ ∗ ( 69 ) = tlh [ 1 2 aclh ( 2148 3 + 3720 + 30 2 + 17 6 ) ] 2 {\displaystyle \lambda ^{*}(69)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\sqrt {2148{\sqrt {3}}+3720}}+30{\sqrt {2}}+17{\sqrt {6}})]^{2}} λ ∗ ( 77 ) = tlh [ 1 2 aclh ( 2276 11 + 7544 + 44 2 + 13 22 ) ] 2 {\displaystyle \lambda ^{*}(77)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\sqrt {2276{\sqrt {11}}+7544}}+44{\sqrt {2}}+13{\sqrt {22}})]^{2}} λ ∗ ( 85 ) = tlh [ 1 2 aclh ( 30 34 + 123 2 ) ] 2 {\displaystyle \lambda ^{*}(85)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(30{\sqrt {34}}+123{\sqrt {2}})]^{2}} λ ∗ ( 93 ) = tlh [ 1 2 aclh ( 100 6 + 171 2 ) ] 2 {\displaystyle \lambda ^{*}(93)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(100{\sqrt {6}}+171{\sqrt {2}})]^{2}}
Bringsches Radikal Auch für die Darstellung des Bringschen Radikals BR in elliptischer Form[ 3] Elliptischem Nomen und Thetafunktion beziehungsweise Weberscher Modulfunktion muss der zugehörige elliptische Modul ermittelt werden.
Die sogenannte Bring-Jerrard-Form der quintischen Gleichungen beinhaltet ein quintisches Glied, ein lineares Glied und ein absolutes Glied:
x 5 + x = u {\displaystyle x^{5}+x=u} Der elliptische Modul und sein Pythagoräisches Gegenstück für diese Gleichung werden beim Bringschen Radikal nach Charles Hermite auf folgende Weise hervorgerufen:
k = tlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 {\displaystyle k={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}} k ′ = ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 {\displaystyle k'={\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}} x = W R 5 ( k ) − W R 5 ( k ′ ) 10 k k ′ 5 [ W R 5 ( k ) + W R 5 ( k ′ ) − 1 ] − [ 2 W R 5 ( k ) + 1 ] [ 2 W R 5 ( k ′ ) + 1 ] {\displaystyle x={\frac {W_{R5}(k)-W_{R5}(k')}{\sqrt {10\,k\,k'}}}\,{\sqrt {{\sqrt {5}}\,[W_{R5}(k)+W_{R5}(k')-1]-{\sqrt {[2\,W_{R5}(k)+1][2\,W_{R5}(k')+1]}}}}} Wichtiger Hinweis über die Definition der reduzierten Weberschen Modulfunktion:
W R 5 ( ε ) = 5 ϑ 00 [ q ( ε ) 5 ] 2 2 ϑ 00 [ q ( ε ) ] 2 − 1 2 = dn [ 2 5 K ( ε ) ; ε ] + dn [ 4 5 K ( ε ) ; ε ] {\displaystyle W_{R5}(\varepsilon )={\frac {5\,\vartheta _{00}[q(\varepsilon )^{5}]^{2}}{2\,\vartheta _{00}[q(\varepsilon )]^{2}}}-{\frac {1}{2}}={\text{dn}}{\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}+{\text{dn}}{\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}} Und diese Etafunktionswerte bilden in rationaler Bruch-Kombination nach dem Aufsatz von Prasolov und Solovyev den elliptischen Ausdruck für das Bringsche Radikal. Alternativ kann das Bringsche Radikal auch mit den Rogers-Ramanujan-Kettenbruchfunktionen R und S dargestellt werden. Vom komplementären Modul müssen im Anschluss das elliptische Nomen für die elliptische Darstellung der Lösung aufgestellt werden. Von diesem Nomen müssen dann nach Prasolov und Solovyev die fünfte Potenz und die fünfte Wurzel in die Thetafunktionen eingesetzt werden. Mit folgendem Verfahren kann auf der Grundlage der genannten Thetafunktionen und des Rogers-Ramanujan-Kettenbruchs die Lösung derselben Gleichung bestimmt werden:
x = S ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } ⟩ 2 − R ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } 2 ⟩ S ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } ⟩ 2 × {\displaystyle x={\frac {S{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}{\bigr \rangle }^{2}-R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}^{2}{\bigr \rangle }}{S{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}{\bigr \rangle }^{2}}}\times } × 1 − R ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } 2 ⟩ S ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } ⟩ R ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } 2 ⟩ 2 × {\displaystyle \times {\frac {1-R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}^{2}{\bigr \rangle }\,S{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}{\bigr \rangle }}{R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}^{2}{\bigr \rangle }^{2}}}\times } × ϑ 00 ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } 5 ⟩ ϑ 00 ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } 1 / 5 ⟩ 2 − 5 ϑ 00 ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } 5 ⟩ 3 2 20 4 sl [ 1 2 2 aclh ( 5 4 5 4 u ) ] ϑ 00 ⟨ q { ctlh [ 1 2 aclh ( 5 4 5 4 u ) ] 2 } ⟩ 3 {\displaystyle \times {\frac {\vartheta _{00}{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}^{5}{\bigr \rangle }\,\vartheta _{00}{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}^{1/5}{\bigr \rangle }^{2}-5\,\vartheta _{00}{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}^{5}{\bigr \rangle }^{3}}{2{\sqrt[{4}]{20}}\,{\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]\,\vartheta _{00}{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,u)]^{2}\}{\bigr \rangle }^{3}}}}
Reduzierte Webersche Modulfunktion Für die reduzierte Webersche Modulfunktion gilt folgendes W R 5 {\displaystyle W_{R5}}
W R 5 { ctlh [ 1 2 aclh ( 1 4 x 5 + 5 4 x ) ] 2 } W R 5 { tlh [ 1 2 aclh ( 1 4 x 5 + 5 4 x ) ] 2 } = {\displaystyle W_{R5}{\bigl \{}{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}{\bigl (}{\tfrac {1}{4}}x^{5}+{\tfrac {5}{4}}x{\bigr )}{\bigr ]}^{2}{\bigr \}}\,W_{R5}{\bigl \{}{\text{tlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}{\bigl (}{\tfrac {1}{4}}x^{5}+{\tfrac {5}{4}}x{\bigr )}{\bigr ]}^{2}{\bigr \}}=} = 4 15 cot { 1 3 arccot [ 1 45 15 ( x 2 x 12 + 18 x 8 + 113 x 4 + 256 + x 8 + 7 x 4 + 11 ) ] } + 8 x 4 + 28 x 12 + 12 x 8 + 43 x 4 + 32 + ( x 6 + 3 x 2 ) x 12 + 18 x 8 + 113 x 4 + 256 {\displaystyle ={\frac {4\,{\sqrt {15}}\cot {\bigl \{}{\tfrac {1}{3}}\operatorname {arccot} {\bigl [}{\tfrac {1}{45}}{\sqrt {15}}{\bigl (}x^{2}{\sqrt {x^{12}+18\,x^{8}+113\,x^{4}+256}}+x^{8}+7\,x^{4}+11{\bigr )}{\bigr ]}{\bigr \}}+8\,x^{4}+28}{x^{12}+12\,x^{8}+43\,x^{4}+32+(x^{6}+3\,x^{2}){\sqrt {x^{12}+18\,x^{8}+113\,x^{4}+256}}}}} In der Areacosinus-Hyperbolicus-Klammer steht ein quintisches Polynom in der Bring-Jerrard-Form.
Ableitungen Der Sinus lemniscatus hyperbolicus hat diese Ableitung:
d d x s l h ( x ) = s l h ( x ) 4 + 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {slh} \,(x)={\sqrt {\mathrm {slh} \,(x)^{4}+1}}} Der Kosinus lemniscatus hyperbolicus hat jene Ableitung:
d d x c l h ( x ) = − c l h ( x ) 4 + 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {clh} \,(x)=-{\sqrt {\mathrm {clh} \,(x)^{4}+1}}} Die Richtigkeit dieser beiden Ableitungen kann auch mit der Quotientenregel so gezeigt werden:
d d x s l h ( x ) = d d x t l h ( x ) c t l h ( x ) = t l h ′ ( x ) c t l h ( x ) − t l h ( x ) c t l h ′ ( x ) c t l h ( x ) 2 = 1 c t l h ( x ) 2 = s l h ( x ) 4 + 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {slh} (x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {tlh} (x)}{\mathrm {ctlh} (x)}}={\frac {\mathrm {tlh} '(x)\,\mathrm {ctlh} (x)-\mathrm {tlh} (x)\,\mathrm {ctlh} '(x)}{\mathrm {ctlh} (x)^{2}}}={\frac {1}{\mathrm {ctlh} (x)^{2}}}={\sqrt {\mathrm {slh} (x)^{4}+1}}} d d x c l h ( x ) = d d x c t l h ( x ) t l h ( x ) = c t l h ′ ( x ) t l h ( x ) − c t l h ( x ) t l h ′ ( x ) t l h ( x ) 2 = − 1 t l h ( x ) 2 = − c l h ( x ) 4 + 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {clh} (x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {ctlh} (x)}{\mathrm {tlh} (x)}}={\frac {\mathrm {ctlh} '(x)\,\mathrm {tlh} (x)-\mathrm {ctlh} (x)\,\mathrm {tlh} '(x)}{\mathrm {tlh} (x)^{2}}}=-{\frac {1}{\mathrm {tlh} (x)^{2}}}=-{\sqrt {\mathrm {clh} (x)^{4}+1}}}
Spezielle Werte Einzelne Funktionswerte für den Sinus lemniscatus hyperbolicus:
s l h ( ϖ 2 2 ) = 1 {\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{2{\sqrt {2}}}}\right)=1} s l h ( ϖ 3 2 ) = 1 3 4 2 3 − 3 4 {\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{3{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{3}}}{\sqrt[{4}]{2{\sqrt {3}}-3}}} s l h ( 2 ϖ 3 2 ) = 2 3 + 3 4 {\displaystyle \mathrm {slh} \,\left({\frac {2\varpi }{3{\sqrt {2}}}}\right)={\sqrt[{4}]{2{\sqrt {3}}+3}}} s l h ( ϖ 4 2 ) = 1 2 4 ( 2 + 1 − 1 ) {\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}-1)} s l h ( 3 ϖ 4 2 ) = 1 2 4 ( 2 + 1 + 1 ) {\displaystyle \mathrm {slh} \,\left({\frac {3\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}+1)} s l h ( ϖ 5 2 ) = 1 8 4 5 − 1 20 4 − 5 + 1 = 2 5 − 2 4 sin ( 1 20 π ) sin ( 3 20 π ) {\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}} s l h ( 2 ϖ 5 2 ) = 1 2 2 4 ( 5 + 1 ) 20 4 − 5 + 1 = 2 5 + 2 4 sin ( 1 20 π ) sin ( 3 20 π ) {\displaystyle \mathrm {slh} \,\left({\frac {2\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}} s l h ( 3 ϖ 5 2 ) = 1 8 4 5 − 1 20 4 + 5 + 1 = 2 5 − 2 4 cos ( 1 20 π ) cos ( 3 20 π ) {\displaystyle \mathrm {slh} \,\left({\frac {3\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}} s l h ( 4 ϖ 5 2 ) = 1 2 2 4 ( 5 + 1 ) 20 4 + 5 + 1 = 2 5 + 2 4 cos ( 1 20 π ) cos ( 3 20 π ) {\displaystyle \mathrm {slh} \,\left({\frac {4\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}} s l h ( ϖ 6 2 ) = 1 2 ( 2 3 + 3 + 1 ) ( 1 − 2 3 − 3 4 ) {\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1-{\sqrt[{4}]{2{\sqrt {3}}-3}})} s l h ( 5 ϖ 6 2 ) = 1 2 ( 2 3 + 3 + 1 ) ( 1 + 2 3 − 3 4 ) {\displaystyle \mathrm {slh} \,\left({\frac {5\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1+{\sqrt[{4}]{2{\sqrt {3}}-3}})}
Bestimmte Integrale
Zusammenhang mit den elliptischen Integralen zweiter und dritter Art Einige bestimmte Integrale sind mit dem hyperbolisch lemniskatischen Areasinus verwandt. Zwei solche bedeutenden Integrale sollen im nun Folgenden hergeleitet werden. Das im Folgenden als Erstes hergeleitete Integral ist als bestimmtes Integral ein elliptisches Integral erster Art. Aber als unbestimmtes Integral ist es ein elliptisches Integral dritter Art. Das im Anschluss als Zweites hergeleitete Integral ist ein elliptisches Integral zweiter Art, welches die Bogenmaße einer Ellipse mit einem Halbachsenverhältnis der Quadratwurzel aus Zwei beschreibt.
Erstes Integral ∫ 0 ∞ 1 ( x 2 + 1 ) x 4 + 1 d x = 1 2 K ( 1 2 2 ) = aslh ( 1 ) {\displaystyle \int _{0}^{\infty }{\frac {1}{(x^{2}+1){\sqrt {x^{4}+1}}}}\,\mathrm {d} x={\frac {1}{2}}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}={\text{aslh}}(1)} Beweis des ersten Integrals:
Definiert sei folgende Funktion:
I ( x ) = ∫ 0 1 x ( x 2 y 2 + 1 ) x 4 y 4 + 1 d y {\displaystyle I(x)=\int _{0}^{1}{\frac {x}{(x^{2}y^{2}+1){\sqrt {x^{4}y^{4}+1}}}}\,\mathrm {d} y} Dann gilt:
d d x I ( x ) = 1 ( x 2 + 1 ) x 4 + 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}I(x)={\frac {1}{(x^{2}+1){\sqrt {x^{4}+1}}}}} I ( 0 ) = 0 {\displaystyle I(0)=0} Und dann gilt auch:
d d x [ I ( x 2 + 1 + x ) − I ( x 2 + 1 − x ) ] = 1 ( 2 x 2 + 1 ) ( 2 x 2 + 2 ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\bigl [}I({\sqrt {x^{2}+1}}+x)-I({\sqrt {x^{2}+1}}-x){\bigr ]}={\frac {1}{\sqrt {(2x^{2}+1)(2x^{2}+2)}}}} I ( x 2 + 1 + x ) − I ( x 2 + 1 − x ) = aslh ( x 2 + 1 + x ) − aslh ( 1 ) {\displaystyle I({\sqrt {x^{2}+1}}+x)-I({\sqrt {x^{2}+1}}-x)={\text{aslh}}({\sqrt {x^{2}+1}}+x)-{\text{aslh}}(1)} I ( x 2 + 1 + x ) − I ( x 2 + 1 − x ) = aslh ( 2 x 2 x 2 + 1 + 1 ) {\displaystyle I({\sqrt {x^{2}+1}}+x)-I({\sqrt {x^{2}+1}}-x)={\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {2x^{2}+1}}+1}}{\bigr )}} lim x → + ∞ [ I ( x 2 + 1 + x ) − I ( x 2 + 1 − x ) ] = aslh ( 1 ) {\displaystyle \lim _{x\rightarrow +\infty }{\bigl [}I({\sqrt {x^{2}+1}}+x)-I({\sqrt {x^{2}+1}}-x){\bigr ]}={\text{aslh}}(1)} ∫ 0 ∞ 1 ( x 2 + 1 ) x 4 + 1 d x = aslh ( 1 ) {\displaystyle \int _{0}^{\infty }{\frac {1}{(x^{2}+1){\sqrt {x^{4}+1}}}}\,\mathrm {d} x={\text{aslh}}(1)} QUOD ERAT DEMONSTRANDUM
Zweites Integral ∫ 0 1 x 4 + 1 ( x 2 + 1 ) 2 d x = 1 2 E ( 1 2 2 ) = 1 2 aslh ( 1 ) + π 16 aslh ( 1 ) {\displaystyle \int _{0}^{1}{\frac {\sqrt {x^{4}+1}}{(x^{2}+1)^{2}}}\,\mathrm {d} x={\frac {1}{2}}E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}={\frac {1}{2}}{\text{aslh}}(1)+{\frac {\pi }{16\,{\text{aslh}}(1)}}} Beweis des zweiten Integrals:
Definiert sei folgende Funktion:
aslh ∗ ( x ) = 1 2 E [ 2 arctan ( x ) ; 1 2 2 ] {\displaystyle {\text{aslh}}^{*}(x)={\tfrac {1}{2}}E[2\arctan(x);{\tfrac {1}{2}}{\sqrt {2}}]} Diese elliptisch verwandte Abwandlung des Areasinus lemniscatus hyperbolicus vom elliptischen Integral erster Art hin zum elliptischen Integral zweiter Art hat dann folgende Ableitung:
d d x aslh ∗ ( x ) = x 4 + 1 ( x 2 + 1 ) 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,{\text{aslh}}^{*}(x)={\frac {\sqrt {x^{4}+1}}{(x^{2}+1)^{2}}}} Und dann gilt auch:
d d x [ 2 2 aslh ∗ ( 2 x 1 + x 2 + 1 − x 2 ) − 2 aslh ( 2 x 1 + x 2 + 1 − x 2 ) − x 1 − x 2 1 + x 2 ] = x 2 1 − x 4 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\biggl [}2{\sqrt {2}}\,{\text{aslh}}^{*}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}-{\sqrt {2}}\,{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}-{\frac {x{\sqrt {1-x^{2}}}}{\sqrt {1+x^{2}}}}{\biggr ]}={\frac {x^{2}}{\sqrt {1-x^{4}}}}} d d x 2 aslh ( 2 x 1 + x 2 + 1 − x 2 ) = 1 1 − x 4 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\sqrt {2}}\,{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}={\frac {1}{\sqrt {1-x^{4}}}}} ∫ 0 1 x 2 1 − x 4 d x = 2 2 aslh ∗ ( 1 ) − 2 aslh ( 1 ) {\displaystyle \int _{0}^{1}{\frac {x^{2}}{\sqrt {1-x^{4}}}}\mathrm {d} x=2{\sqrt {2}}\,{\text{aslh}}^{*}(1)-{\sqrt {2}}\,{\text{aslh}}(1)} ∫ 0 1 1 1 − x 4 d x = 2 aslh ( 1 ) {\displaystyle \int _{0}^{1}{\frac {1}{\sqrt {1-x^{4}}}}\mathrm {d} x={\sqrt {2}}\,{\text{aslh}}(1)} Der Satz von Fubini liefert folgendes Resultat:
∫ 0 1 1 1 − x 4 d x ∫ 0 1 x 2 1 − x 4 d x = ∫ 0 1 ( 1 1 − x 4 ∫ 0 1 x 3 y 2 1 − x 4 y 4 d y + x 2 1 − x 4 ∫ 0 1 x 1 − x 4 y 4 d y ) d x = {\displaystyle \int _{0}^{1}{\frac {1}{\sqrt {1-x^{4}}}}\mathrm {d} x\int _{0}^{1}{\frac {x^{2}}{\sqrt {1-x^{4}}}}\mathrm {d} x=\int _{0}^{1}{\biggl (}{\frac {1}{\sqrt {1-x^{4}}}}\int _{0}^{1}{\frac {x^{3}y^{2}}{\sqrt {1-x^{4}y^{4}}}}\mathrm {d} y+{\frac {x^{2}}{\sqrt {1-x^{4}}}}\int _{0}^{1}{\frac {x}{\sqrt {1-x^{4}y^{4}}}}\mathrm {d} y{\biggr )}\mathrm {d} x=} = ∫ 0 1 ∫ 0 1 x 3 ( y 2 + 1 ) ( 1 − x 4 ) ( 1 − x 4 y 4 ) d y d x = ∫ 0 1 ∫ 0 1 x 3 ( y 2 + 1 ) ( 1 − x 4 ) ( 1 − x 4 y 4 ) d x d y = ∫ 0 1 y 2 + 1 2 y 2 artanh ( y 2 ) d y = π 4 {\displaystyle =\int _{0}^{1}\int _{0}^{1}{\frac {x^{3}(y^{2}+1)}{\sqrt {(1-x^{4})(1-x^{4}y^{4})}}}\mathrm {d} y\,\mathrm {d} x=\int _{0}^{1}\int _{0}^{1}{\frac {x^{3}(y^{2}+1)}{\sqrt {(1-x^{4})(1-x^{4}y^{4})}}}\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}{\frac {y^{2}+1}{2y^{2}}}\operatorname {artanh} (y^{2})\mathrm {d} y={\frac {\pi }{4}}} Hiermit zusammenhängend gilt natürlich auch:
aslh ( 2 x 1 + x 2 + 1 − x 2 ) [ 2 aslh ∗ ( 2 x 1 + x 2 + 1 − x 2 ) − aslh ( 2 x 1 + x 2 + 1 − x 2 ) − x 1 − x 2 2 + 2 x 2 ] = {\displaystyle {\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}{\biggl [}2\,{\text{aslh}}^{*}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}-{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}-{\frac {x{\sqrt {1-x^{2}}}}{\sqrt {2+2x^{2}}}}{\biggr ]}=} = ∫ 0 1 y 2 + 1 4 y 2 [ artanh ( y 2 ) − artanh ( 1 − x 4 y 2 1 − x 4 y 4 ) ] d y {\displaystyle =\int _{0}^{1}{\frac {y^{2}+1}{4y^{2}}}{\biggl [}{\text{artanh}}(y^{2})-{\text{artanh}}{\bigl (}{\frac {{\sqrt {1-x^{4}}}\,y^{2}}{\sqrt {1-x^{4}y^{4}}}}{\bigr )}{\biggr ]}\mathrm {d} y} Die Richtigkeit dieser soeben genannten Formel kann durch die Ableitung beider Seiten der Gleichungswaage bezüglich x bestätigt werden.
Wenn der Wert x = 1 in die genannte Formel eingesetzt wird, dann entsteht folgendes Ergebnis:
aslh ( 1 ) [ 2 aslh ∗ ( 1 ) − aslh ( 1 ) ] = 1 8 π {\displaystyle {\text{aslh}}(1){\bigl [}2\,{\text{aslh}}^{*}(1)-{\text{aslh}}(1){\bigr ]}={\tfrac {1}{8}}\pi } ∫ 0 1 x 4 + 1 ( x 2 + 1 ) 2 d x = aslh ∗ ( 1 ) {\displaystyle \int _{0}^{1}{\frac {\sqrt {x^{4}+1}}{(x^{2}+1)^{2}}}\,\mathrm {d} x={\text{aslh}}^{*}(1)} ∫ 0 1 x 4 + 1 ( x 2 + 1 ) 2 d x = 1 2 aslh ( 1 ) + π 16 aslh ( 1 ) {\displaystyle \int _{0}^{1}{\frac {\sqrt {x^{4}+1}}{(x^{2}+1)^{2}}}\,\mathrm {d} x={\frac {1}{2}}{\text{aslh}}(1)+{\frac {\pi }{16\,{\text{aslh}}(1)}}} QUOD ERAT DEMONSTRANDUM
Siehe auch
Literatur Edward Neuman: Two-sided inequalitites for the lemniscate functions. Volume 1, Southern Illinois University Carbondale , USA, 2014. Ji-en Deng und Chao-ping Chen: Sharp Shafer-Fink type inequalities for Gauss lemniscate functions. Universität Henan (河南大学), China, 2014. Jun-Ling Sun und Chao-ping Chen: Shafer-type inequalities for inverse trigonometric functions and Gauss lemniscate functions. Universität Henan, China, 2016. Minjie Wei, Yue He und Gendi Wang: Shafer-Fink type inequalities for arc lemniscate functions. Hangzhou, China, 2019. Bruce Berndt : Ramanujan’s Notebooks, Part IV. New York: Springer-Verlag, 1994. Seiten 255–258.Charles Hermite : Sulla risoluzione delle equazioni del quinto grado. Annali di math. pura ed appl. 1, 1858. Seite 258.Viktor Prasolov (Прасолов) und Yuri Solovyev (Соловьёв): Elliptic Functions and Elliptic Integrals. Volume 170, Rhode Island 1991. Seiten 149–159.
Einzelnachweise ↑ Eric W. Weisstein : Hyperbolic Lemniscate Function .MathWorld ↑ Wei-Mao Qian, Miao-Kun Wang, Wei-Mao Qian, Miao-Kun Wang: Sharp bounds for Gauss Lemniscate functions and Lemniscatic means . In: AIMS Mathematics . Band 6 , Nr. 7 , 2021, ISSN 2473-6988 S. 7479–7493 , doi :10.3934/math.2021437 aimspress.com [abgerufen am 24. Oktober 2021]). ↑ F. Brioschi: Sulla risoluzione delle equazioni del quinto grado: Hermite – Sur la résolution de l’Équation du cinquiéme degré Comptes rendus –. N. 11. Mars. 1858 . 1. Dezember 1858, doi :10.1007/bf03197334 zenodo.org [abgerufen am 24. Oktober 2021]).