Hyperbelzirkel des Frans van Schooten

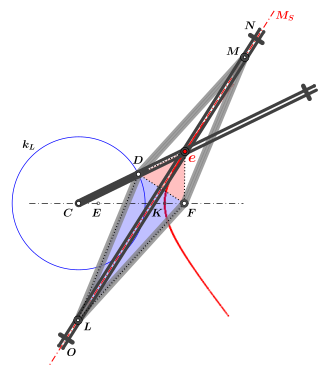
Der Hyperbelzirkel des Frans van Schooten ist ein Mechanismus, der die Form einer Hyperbel erzeugt. Im Jahr 1657 veröffentlichte Frans van Schooten in seinem Werk Exercitationum mathematicarum libri quinque^[1] in LIBER IV^[2] einen Hyperbelzirkel.^[3] Er ähnelt dem Ellipsenzirkel des Frans van Schooten.

Im Wesentlichen besteht der Hyperbelzirkel aus drei Teilen:

1. einer Raute mit den Gelenkpunkten ${\displaystyle DLFM,}$ mit der ersten Zirkelnadel im Brennpunkt ${\displaystyle F}$,
2. einer Diagonalschiene ${\displaystyle |NO|}$ aus zwei an den Enden verbundenen Stäben, mit dem Schreibstift in ${\displaystyle e,}$
3. einer Führungsschiene mit der zweiten Zirkelnadel im Punkt ${\displaystyle C}$. Die Führungsschiene ist nach dem Gelenkpunkt ${\displaystyle D}$ geschlitzt und verläuft durch den Punkt ${\displaystyle e}$.

Drei sogenannte Gleitsteine ermöglichen linear bewegliche Verbindungen. Einer davon führt den Gelenkpunkt ${\displaystyle L}$ der Raute, der zweite den Schreibstift im Punkt ${\displaystyle e}$ und der dritte Gleitstein führt den Gelenkpunkt ${\displaystyle M}$ der Raute. Die Diagonalschiene ${\displaystyle |NO|}$ ist nicht in einem Gelenkpunkt ${\displaystyle |M|}$ oder ${\displaystyle |L|}$ der Raute gelagert, sie ist deshalb in Längsrichtung von ${\displaystyle O}$ bis ${\displaystyle L}$ und von ${\displaystyle N}$ bis ${\displaystyle M}$ verschiebbar. Im Vergleich dazu ist im Ellipsenzirkel des Frans van Schooten der Diagonalstab ${\displaystyle |OQ|}$ im Gelenkpunkt ${\displaystyle O}$ der Raute gelagert.

Das Zeichnen einer Hyperbel mithilfe des Zeichenstiftes in ${\displaystyle e}$ soll die Hand verdeutlichen. Nach dem Einstechen des Zirkels in die Brennpunkte ${\displaystyle C}$ und ${\displaystyle F,}$ wird mit einer Hand mithilfe eines Griffes im Punkt ${\displaystyle e}$ der Hyperbelzirkel bewegt. Dabei zwingt die Führungsschiene (${\displaystyle C}$ durch ${\displaystyle D}$ und ${\displaystyle e,}$) zusammen mit der Diagonalschiene ${\displaystyle |NO,|}$ den Schreibstift in ${\displaystyle e}$ in eine hyperbelförmige Bahn.

Aufgrund der Darstellung ist anzunehmen, dass der Hyperbelzirkel in bestimmten labilen Lagen (u. a. wenn Brennpunkte und Zeichenstift auf einer Linie liegen) mit der anderen Hand, am Punkt ${\displaystyle M}$ oder ${\displaystyle L,}$ einer Stützung bedarf.

Eine mögliche Begründung, weshalb die mit dem Hyperbelzirkel des Frans van Schooten gezogenen Kurven exakte Hyperbeln sind, ist im nachfolgenden Abschnitt Geometrische Betrachtung beschrieben.

Geometrische Betrachtung

Zur Verdeutlichung, weshalb die mit dem Hyperbelzirkel erzeugten Kurven exakte Hyperbeln sind, wird im Folgenden zuerst in einer Basiskonstruktion ein Hyperbelpunkt ${\displaystyle e}$ nach Definition mit Leitkreis bestimmt und im Anschluss daran der Hyperbelzirkel prinzipiell eingearbeitet. In Hyperbel zeichnen wird dessen Bewegungsablauf erläutert. Die Bezeichnungen der Punkte sind der obigen originären Darstellung Hyperbelzirkel des Frans van Schooten entnommen.

Hyperbelpunkt nach Definition mit Leitkreis

Mit den von Bild 1 eingesetzten Bezeichnungen der Punkte, lautet eine maßgebende Aussage der Definition mit Leitkreis, bezogen auf den rechten Ast der Hyperbel:

„Ist ${\displaystyle k_{L}}$ der Kreis um ${\displaystyle C}$ mit Radius ${\displaystyle 2a}$, so hat ${\displaystyle e}$ vom Kreis ${\displaystyle k_{L}}$ denselben Abstand wie vom Brennpunkt ${\displaystyle F}$: ${\displaystyle |ek_{L}|=|eF|\ .}$ Man nennt ${\displaystyle k_{L}}$ den zu ${\displaystyle F}$ gehörigen Leitkreis der Hyperbel.“

Es beginnt mit dem Einzeichnen einer Geraden, der Mittelachse der späteren Hyperbel. Darauf wird der erste Scheitelpunkt ${\displaystyle E}$ beliebig markiert und anschließend, mit einem frei wählbaren Abstand, der zweite Scheitelpunkt ${\displaystyle K}$ festgelegt. Somit ist der Abstand ${\displaystyle |EK|}$ der Scheitelpunkte, gleichbedeutend mit dem Radius ${\displaystyle 2a}$ des Leitkreises ${\displaystyle k_{L},}$ bestimmt. Nun setzt man mit einem abgeschätzten, aber gleichen Abstand zu ${\displaystyle E}$ bzw. ${\displaystyle K,}$ jeweils nach außen, die Brennpunkte ${\displaystyle C}$ und ${\displaystyle F.}$ Mit den gewählten Brennpunkten ${\displaystyle C}$ und ${\displaystyle F}$ sowie mit einem der beiden Scheitelpunkte ${\displaystyle E}$ oder ${\displaystyle K}$ (drei bekannte Punkte) ist die Hyperbel bereits mathematisch bestimmt. Die Hyperbel (grün) kann z. B. mithilfe einer Dynamischen‐Geometrie‐Software (DGS) eingetragen werden.

Es geht weiter mit dem Ziehen des Leitkreises ${\displaystyle k_{L}}$ um ${\displaystyle C}$ mit dem Radius ${\displaystyle |EK|=2a}$ für den rechten Ast der Hyperbel; es ergibt den Hilfspunkt ${\displaystyle A.}$ Um den Punkt ${\displaystyle e}$ zu finden, der zum Brennpunkt ${\displaystyle F}$ den gleichen Abstand hat wie zum Leitkreis ${\displaystyle k_{L},}$ zieht man mit beliebigem Radius, aber mit derselben Zirkelöffnung um ${\displaystyle F}$ den Kreis ${\displaystyle k_{1}}$ und um ${\displaystyle A}$ den Kreis ${\displaystyle k_{2};}$ dabei ergibt sich der zweite Hilfspunkt ${\displaystyle B.}$ Wird jetzt ein Kreis ${\displaystyle k_{3}}$ mit dem Radius ${\displaystyle |CB|}$ um ${\displaystyle C}$ eingezeichnet, wird sozusagen der Radius ${\displaystyle |AB|}$ des Kreises ${\displaystyle k_{2}}$ zum Radius ${\displaystyle |CA|}$ des Leitkreises ${\displaystyle k_{L}}$ addiert. Der Schnittpunkt des Kreises ${\displaystyle k_{3}}$ mit ${\displaystyle k_{1}}$ ist der gesuchte Punkt ${\displaystyle e.}$

Die nun folgende Halbgerade ${\displaystyle H_{G}}$ ab ${\displaystyle C}$ durch ${\displaystyle e}$ schneidet den Leitkreis ${\displaystyle k_{L}}$ in ${\displaystyle D}$ und liefert das gleichschenklige Dreieck ${\displaystyle DFe}$ (rosa) mit den beiden gleich langen Seitenlängen ${\displaystyle {\overline {eD}}}$ und ${\displaystyle {\overline {eF}}.}$ Abschließend wird noch die Mittelsenkrechte ${\displaystyle M_{S}}$ des Abstandes ${\displaystyle |DF|}$ eingetragen; wegen des gleichschenkligen Dreiecks ${\displaystyle DFe}$ verläuft sie durch den Punkt ${\displaystyle e.}$ Daraus folgt:

das gleichschenklige Dreieck ${\displaystyle DFe}$ mit

${\displaystyle |eD|=|eF|,}$

ist eine halbe Raute, in der die Mittelsenkrechte ${\displaystyle M_{S}}$ und die Winkelhalbierende des Winkels ${\displaystyle DeF}$ Tangenten der Hyperbel sind. Somit ist der konstruierte Punkt ${\displaystyle e}$ ein Hyperbelpunkt.

Konstruktion des Hyperbelzirkels

• Damit der Hyperbelzirkel eine komplette Hyperbellinie zeichnen kann, ist es erforderlich, dass die Führungsschiene (ab ${\displaystyle C}$ durch ${\displaystyle D}$) oberhalb der Raute ${\displaystyle DLFM}$ (Zirkelnadel in ${\displaystyle F}$) liegt. Anzumerken ist, in der obigen originären Darstellung Hyperbelzirkel des Frans van Schooten liegt die Führungsschiene unterhalb der Raute. Mit dieser Position der Führungsschiene kann die Hyperbellinie nicht durch den Scheitelpunkt ${\displaystyle K}$ gezogen werden, sondern nur, z. B. gegen den Uhrzeigersinn, bis die Führungsschiene an der Zirkelnadel in ${\displaystyle F}$ der Raute anliegt.

Die Prinzipskizze (Bild 2) ist eine Weiterführung der Basiskonstruktion Hyperbelpunkt nach Definition mit Leitkreis ${\displaystyle k_{L}}$ (Bild 1). Für eine bessere Übersichtlichkeit wurden die irrelevanten Kreise, Punkte etc. ausgeblendet. Der Leitkreis ${\displaystyle k_{L}}$ sowie u. a. die Punkte ${\displaystyle D}$ und ${\displaystyle F}$ sind bereits in der vorangegangenen Konstruktion (Bild 1) bestimmt, es bedarf deshalb nur noch einer einfachen Einarbeitung der obig beschriebenen wesentlichen Teile des Hyperbelzirkels.

Zuerst werden die zwei Seitenlängen ${\displaystyle {\overline {FM}}}$ und ${\displaystyle {\overline {FL}}}$ der Raute, mit abgeschätzter Zirkelöffnung, deutlich größer als der Abstand ${\displaystyle |Fe|}$, auf der Mittelsenkrechten ${\displaystyle M_{S}}$ festgelegt. Die Verbindung der Gelenkpunkte ${\displaystyle D}$ mit ${\displaystyle M}$ sowie ${\displaystyle D}$ mit ${\displaystyle L}$ schließt sich an und vollendet die Raute ${\displaystyle FMDL}$ mit dem gleichschenkligen Dreieck ${\displaystyle FDL}$ (hellblau). Es folgt das Einzeichnen der Diagonalschiene, deren Länge ${\displaystyle {\overline {NO}}}$ größer ist, als die Diagonale ${\displaystyle |LM|}$ der Raute. Abschließend wird die Führungsschiene ab ${\displaystyle C}$ durch ${\displaystyle D}$ eingezeichnet. Sie schneidet die Diagonalschiene ${\displaystyle |NO|}$, wie vorgegeben, ebenfalls im Hyperbelpunkt ${\displaystyle e}$ des gleichschenkligen Dreiecks ${\displaystyle DFe}$ (rosa).

Bild 2: Prinzipskizze, Führungsschiene
(ab ${\displaystyle C}$ durch ${\displaystyle D}$) liegt oberhalb der Raute ${\displaystyle DLFM}$

Animation der Prinzipskizze

Hyperbel zeichnen

Wird der Hyperbelzirkel wie oben beschrieben von Hand bewegt, läuft der Punkt ${\displaystyle D}$ auf dem Leitkreis ${\displaystyle k_{L}}$ und der Schreibstift (${\displaystyle e}$) im Spalt der Diagonalschiene ${\displaystyle |NO|.}$ Die Führungsschiene (${\displaystyle C}$ durch ${\displaystyle D}$ und ${\displaystyle e}$) zwingt die Diagonalschiene ${\displaystyle |NO|}$ als konstante Mittelsenkrechte ${\displaystyle M_{S},}$ der sich kontinuierlich verändernden gleichschenkligen Dreiecke ${\displaystyle FDL}$ und ${\displaystyle DFe}$, zu wirken. Daraus folgt: In jeder gedrehten Stellung des Parabelzirkels gilt

${\displaystyle |eD|=|eF|}$

Damit wird aufgezeigt: Die mit dem Hyperbelzirkel gezogenen Kurven sind exakte Hyperbeln.

Siehe auch

Fadenkonstruktion einer Hyperbel

Literatur

• C. Edward Sandifer: Van Schooten’s Ruler Constructions. In: Convergence August 2010. August 2010, doi:10.4169/convergence20141101 (englisch, Onlineversion vom November 2014). 

Einzelnachweise

1. ↑ Frans van Schooten: Exercitationum mathematicarum libri quinque. Lugdunum Batavorum (= Johannes Elsevir, Leiden 1657, Inhaltsübersicht, books.google.de).
2. ↑ Frans van Schooten: Exercitationum mathematicarum libri V. Buch IV. Johannes Elsevir, Leiden 1657 S. 293 (books.google.de).
3. ↑ Frans van Schooten: Exercitationum mathematicarum libri V. Band IV. Johannes Elsevir, Leiden 1657, S. 349 (books.google.de).