Hyperbelbewegung

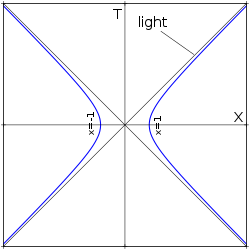
Die Hyperbelbewegung beschleunigter Objekte entlang der ${\displaystyle X}$-Achse kann mittels Minkowski-Diagramm visualisiert werden. Jede Hyperbel wird definiert durch ${\displaystyle x=\pm c^{2}/\alpha }$ und ${\displaystyle \eta =\alpha \tau /c}$ (mit ${\displaystyle c=1,\alpha =1}$) in Gleichung  (2)

Die Hyperbelbewegung ist in der speziellen Relativitätstheorie die Bewegung eines Objekts mit konstanter Eigenbeschleunigung, wobei diese Beschleunigung von einem mitbewegten Beobachter mittels Beschleunigungssensor gemessen wird. Der Name Hyperbelbewegung folgt aus dem Umstand, dass die Gleichung für den Pfad dieses Objekts im Minkowski-Diagramm einer Hyperbel entspricht. Diese Bewegung hat einige interessante Eigenschaften, wie die Möglichkeit, das Licht hinter sich zu lassen, wenn ein genügender Vorsprung gegeben ist.^[1] Für einen allgemeinen Überblick zu Beschleunigungen in der Minkowski-Raumzeit siehe Beschleunigung (Spezielle Relativitätstheorie).

Darüber hinaus ist es möglich, diese Bewegung durch Benutzung hyperbolischer Koordinaten in einem beschleunigten Bezugssystem darzustellen.^[1][2][3][4] Diese Koordinaten können weiter unterteilt werden bezüglich der Position des beschleunigten Beobachters oder der benutzten Längenmessung. Bekannt sind dabei die Ausdrücke Rindler-Koordinaten,^[5] Møller-Koordinaten,^[6] Kottler-Møller-Koordinaten,^[7] Radar-Koordinaten,^[2] Lass-Koordinaten,^[8][9] wobei alle diese Systeme häufig nur als Rindler-Koordinaten bezeichnet werden.^[10]

Die Hyperbelbewegung und das hyperbolisch beschleunigte Bezugssystem wurden bereits in der Frühzeit der SRT, oft im Zusammenhang mit der Bornschen Starrheit, diskutiert. Entsprechende Relationen für die flache Raumzeit finden sich bei Albert Einstein (1907, 1912),^{[H 1]} Max Born (1909),^{[H 2]} Gustav Herglotz (1909),^{[H 3]} Arnold Sommerfeld (1910),^{[H 4]} Max von Laue (1911),^{[H 5]} Hendrik Lorentz (1913),^{[H 6]} Friedrich Kottler (1914),^{[H 7]} Wolfgang Pauli (1921),^{[H 8]} Karl Bollert (1922),^{[H 9]} Stjepan Mohorovičić (1922),^{[H 10]} Georges Lemaître (1924),^{[H 11]} Einstein & Nathan Rosen (1935),^{[H 1]} Christian Møller (1943, 1952),^{[H 12]} Fritz Rohrlich (1963),^[11] Harry Lass (1963),^[12] und für die flache als auch gekrümmte Raumzeit der allgemeinen Relativitätstheorie bei Wolfgang Rindler (1960, 1966).^[13][14] Für Details siehe den Abschnitt zur Geschichte.

Weltlinie

Die Eigenbeschleunigung ${\displaystyle \alpha }$ eines Teilchens ist definiert als die Beschleunigung, die es erfährt, wenn es von einem Inertialsystem in ein anderes wechselt. Wenn ${\displaystyle \alpha }$ parallel zur Bewegungsrichtung ist, dann besteht folgende Beziehung zur gewöhnlichen Dreierbeschleunigung ${\displaystyle a=du/dT}$:

${\displaystyle \alpha =\gamma ^{3}a={\frac {1}{\left(1-u^{2}/c^{2}\right)^{3/2}}}{\frac {du}{dT}},}$

wo ${\displaystyle u}$ die momentane Geschwindigkeit des Teilchens ist, ${\displaystyle \gamma }$ der Lorentzfaktor, ${\displaystyle c}$ die Lichtgeschwindigkeit und ${\displaystyle T}$ die Koordinatenzeit, gemessen im externen Inertialsystem. Die daraus durch Integration folgenden Gleichungen der Weltlinie können als Funktion der Koordinatenzeit ${\displaystyle T}$ als auch der Eigenzeit ${\displaystyle \tau }$ des Teilchens ausgedrückt werden. Wenn alle Anfangswerte für Zeit, Ort und Geschwindigkeit auf 0 gesetzt werden, haben sie die folgende Form:^{[15][16][17][18]}

Das Teilchen ist also bei ${\displaystyle X=0}$ zur Zeit ${\displaystyle T=0}$ und beschreibt die Hyperbel ${\displaystyle \left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}}$. Wenn die Anfangswerte allerdings nicht 0 sind, folgt:^[19][20][21]

${\displaystyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {u_{0}\gamma _{0}+\alpha T}{\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}}\quad \\&=c\tanh \left\{\operatorname {asinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right\}\\X(T)&=X_{0}+{\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}-\gamma _{0}\right)\\&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {asinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right]-\gamma _{0}\right\}\\c\tau (T)&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\ln \left({\frac {{\sqrt {c^{2}+\left(u_{0}\gamma _{0}+\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T}{\left(c+u_{0}\right)\gamma _{0}}}\right)\\&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\left\{\operatorname {asinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)-\operatorname {atanh} \left({\frac {u_{0}}{c}}\right)\right\}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh \left\{\operatorname {atanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right\}\\\\X(\tau )&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {atanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-\gamma _{0}\right\}\\\\cT(\tau )&=cT_{0}+{\frac {c^{2}}{\alpha }}\left\{\sinh \left[\operatorname {atanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-{\frac {u_{0}\gamma _{0}}{c}}\right\}\end{aligned}}\end{array}}}$

Rapidität

Zur Vereinfachung kann die Position

${\displaystyle X={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)}$

einer räumlichen Verschiebung um ${\displaystyle c^{2}/\alpha }$ unterzogen werden, also

${\displaystyle X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}}$,^[22]

wodurch das Teilchen an der Position ${\displaystyle X=c^{2}/\alpha }$ zur Zeit ${\displaystyle T=0}$ ist. Wird nun ${\displaystyle x=c^{2}/\alpha }$ und durch Einführung der Rapidität ${\displaystyle \eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}}$ gesetzt,^[21] reduzieren sich die Gleichungen der Hyperbelbewegung auf^{[H 4][H 13]}

mit der Hyperbel ${\displaystyle X^{2}-c^{2}T^{2}=x^{2}}$.

Geladene Teilchen

Born (1909),^{[H 2]} Sommerfeld (1910),^{[H 4]} von Laue (1911)^{[H 5]} und Pauli (1921)^{[H 8]} formulierten auch die Gleichungen für das elektromagnetische Feld geladener Teilchen in Hyperbelbewegung.^[23] Dies wurde fortgeführt durch Hermann Bondi & Thomas Gold (1955)^[24] und Fulton & Fritz Rohrlich (1960)^[25][11]

${\displaystyle {\begin{aligned}E_{\rho '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 'z'}{\xi ^{\prime 3}}}\\E_{z'}'=&{\frac {-\left(4e/\alpha ^{2}\right)1/\alpha ^{2}+t^{\prime 2}+\rho ^{\prime 2}-z^{\prime 2}}{\xi ^{\prime 3}}}\\E_{\varphi '}'=&H_{\varphi '}'=H_{z'}'=0\\H_{\varphi '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 't'}{\xi ^{\prime 3}}}\\\xi '=&{\sqrt {\left(1/\alpha ^{2}+t^{\prime 2}-\rho ^{\prime 2}-z^{\prime 2}\right)^{2}+\left(2\rho '/\alpha \right)^{2}}}\end{aligned}}}$

Dies steht im Zusammenhang mit der kontrovers^[26][27] diskutierten Frage, ob Ladungen in immerwährender Hyperbelbewegung strahlen oder nicht, und ob dies mit dem Äquivalenzprinzip verträglich ist – obwohl es sich nur um eine hypothetische Frage handelt, da eine immer währende Hyperbelbewegung nicht möglich ist. Frühe Autoren wie Born (1909) oder Pauli (1921) gingen davon aus, dass keine Strahlung auftritt, jedoch wurde später von Bondi & Gold^[24] und Fulton & Rohrlich^[25][11] gezeigt, dass sehr wohl Strahlung auftritt.

Rindler-Koordinaten

(c) Dr Greg, CC BY-SA 3.0

Rindler-Koordinaten für ${\displaystyle \alpha =0{,}5}$ in Gleichung  (2), auf einem Minkowski-Diagramm. Die strichlierten Linien entsprechen dem Rindler-Horizont.

In Gleichung  (2) für die Hyperbelbewegung wurde der Ausdruck ${\displaystyle x}$ als Konstante verwendet, wohingegen die Rapidität ${\displaystyle \eta }$ eine Variable ist. Wie beispielsweise Sommerfeld (1910)^{[H 4]} ausführte, kann umgekehrt auch ${\displaystyle x}$ als variabel und ${\displaystyle \eta }$ als konstant angenommen werden. Das bedeutet, dass die Gleichungen eine Transformationen in ein mitbeschleunigtes Bezugssystem darstellen, und somit die Ruhegestalt des beschleunigten Körpers anzeigen. Die Eigenzeit des Beobachters wird dabei zur Koordinatenzeit des hyperbolisch beschleunigten Systems, dessen Koordinaten häufig als Rindler-Koordinaten bezeichnet werden:

${\displaystyle cT=x\sinh \eta ,\quad X=x\cosh \eta ,\quad Y=y,\quad Z=z}$

Durch Benutzung dieser Koordinaten, beispielsweise für die Analyse des Unruh-Effekts, ergibt sich für den Beobachter ein scheinbarer Ereignishorizont, oft als Rindler-Horizont bezeichnet, der die Grenze darstellt, von dem aus der Beobachter keine Lichtsignale mehr erhalten kann.

Eine allgemeinere Herleitung des Eigenbezugssystems (bzw. der Fermi-Koordinaten) für die Hyperbelbewegung folgt durch Verwendung eines begleitenden Vierbeins mittels Frenet-Serret-Formeln oder drehungsfreiem Fermi-Walker-Transport.^[17] Abhängig von der Wahl des Ursprungs können Metrik, Zeitdilatation zwischen der Zeit ${\displaystyle dt_{0}}$ am Ursprung und ${\displaystyle dt}$ am Ort ${\displaystyle x}$, und die Koordinatenlichtgeschwindigkeit ${\displaystyle |dx|/|dt|}$ hergeleitet werden (diese variable Lichtgeschwindigkeit steht nicht im Widerspruch zur Konstanz der Lichtgeschwindigkeit in Inertialsystemen gemäß SRT, da hier ein beschleunigtes Bezugssystem benutzt wird, und somit diese Variabilität ein bloßes Artefakt der benutzten Koordinaten ist). Anstelle eines derart definierten Eigenbezugssystems können auch Radar-Koordinaten benutzt werden, wobei die Entfernungen durch Lichtsignale bestimmt werden – auf diese Weise sind die Ausdrücke für Metrik, Zeitdilatation und Lichtgeschwindigkeit nicht mehr abhängig vom benutzten Koordinatenursprung. Insbesondere ist bei Benutzung von Radar-Koordinaten die Koordinatenlichtgeschwindigkeit immer gleich der Vakuumlichtgeschwindigkeit in Inertialsystemen. In folgender Tabelle werden verschiedene Koordinatensysteme für die Hyperbelbewegung dargestellt (wobei zur Vereinfachung die Lichtgeschwindigkeit gleich 1 gesetzt wird):

Spezielle konforme Transformation

Eine weniger bekannte Methode zur Definition eines Bezugssystems für die Hyperbelbewegung ist die spezielle konforme Transformation, die aus einer Inversion, einer Translation und einer weiteren Inversion besteht. Gewöhnlich wird sie als Eichtransformation in der Minkowski-Raumzeit interpretiert, jedoch wenden manche Autoren sie auch als Beschleunigungstransformation an:^[37]

${\displaystyle X^{\mu }={\frac {x^{\mu }-a^{\mu }x^{2}}{1-2ax+a^{2}x^{2}}}}$

Wird nur eine räumliche Dimension benutzt mit ${\displaystyle x^{\mu }=(t,x)}$, wobei ${\displaystyle x=0}$ gesetzt werden kann, und mit der Beschleunigung ${\displaystyle a^{\mu }=(0,-\alpha /2)}$, dann folgt^[38]

${\displaystyle T={\frac {t}{1-{\frac {1}{4}}\alpha {}^{2}t^{2}}},\quad X={\frac {-\alpha t^{2}}{2\left(1-{\frac {1}{4}}\alpha {}^{2}t^{2}\right)}}}$

mit der Hyperbel ${\displaystyle \left(X-1/\alpha \right)^{2}-T^{2}=1/\alpha ^{2}}$. Es zeigt sich, dass bei ${\displaystyle t=\pm (x+2/\alpha )}$ die Zeit singulär wird, weswegen man dieses Limit gemäß Fulton & Rohrlich & Witten^[38] einfach vermeiden sollte, wohingegen Kastrup^[37] (der sehr kritisch gegenüber der Beschleunigungsinterpretation ist) anmerkt, dass dies eines der „seltsamen“ Resultate dieser Interpretation ist.

Geschichte

Hyperbelbewegung

Hermann Minkowski (1908)^{[H 15]} demonstrierte den Zusammenhang zwischen dem Punkt auf einer Weltlinie, der Norm der Viererbeschleunigung, und einer Krümmungshyperbel. Im Zusammenhang mit seinem Konzept der Bornschen Starrheit, bezeichnete Max Born (1909) den Fall mit konstanter Eigenbeschleunigung als „Hyperbelbewegung“, und gab eine detaillierte Beschreibung von bewegten Ladungen. Borns Formeln wurden von Gustav Herglotz (1909),^{[H 3]} Arnold Sommerfeld (1910)^{[H 4]} und anderen ergänzt und vereinfacht.

Eigenbezugssystem

Albert Einstein (1907)^{[H 16]} studierte die Effekte in einem gleichförmig beschleunigten Bezugssystem, und erhielt die Gleichungen für koordinatenabhängige Zeitdilatation und Lichtgeschwindigkeit äquivalent mit  (2c), und um die Formeln unabhängig vom Beobachterursprung zu machen, die Zeitdilatation  (2i) in Übereinstimmung mit Radar-Koordinaten. Max Born (1909)^{[H 17]} benutzte seine Formeln für die Hyperbelbewegung als Transformationen in ein „hyperbolisch beschleunigtes Bezugssystem“ äquivalent mit  (2d), was von Arnold Sommerfeld (1910)^{[H 18]} und Max von Laue (1911)^{[H 5]} unter Benutzung imaginärer Zahlen fortgeführt wurde. Zusammengefasst wurde das alles von Wolfgang Pauli (1921),^[16] der sowohl  (2d) als auch die Metrik  (2e) mit imaginären Zahlen anführte. Parallel dazu studierte Einstein (1912)^{[H 19]} ein statisches Gravitationsfeld und leitete dabei erstmals die Kottler-Møller-Metrik  (2b) ab, und formulierte Näherungen zu  (2a).^[39] Einstein folgend erhielt auch Hendrik Lorentz (1913)^{[H 20]} ähnliche Koordinaten wie  (2d),  (2e) und  (2f).

Eine detaillierte Beschreibung gab Friedrich Kottler (1914),^{[H 21]} der das entsprechende orthonormale Vierbein, die Transformationsformeln und Metrik  (2a),  (2b) formulierte. Auch Karl Bollert (1922)^{[H 22]} erhielt die Metrik  (2b) in einer Studie über das gleichförmige Gravitationsfeld. In einer Arbeit zur Bornschen Starrheit, erhielt Georges Lemaître (1924)^{[H 23]} Koordinaten und Metrik  (2a),  (2b). Einstein und Nathan Rosen (1935) beschrieben  (2d),  (2e) als die „wohlbekannten“ Ausdrücke für ein homogenes Gravitationsfeld.^{[H 24]} Nachdem Christian Møller (1943)^{[H 12]} Gleichungen  (2a),  (2b) in einer Studie über homogene Gravitationsfelder erhalten hatte, benutzten er selbst (1952)^{[H 25]} als auch Misner & Thorne & Wheeler (1973)^[1] zur Herleitung derselben Gleichungen die Gleichungen für den Fermi-Walker-Transport.

Während obige Studien auf die flache Minkowski-Raumzeit beschränkt waren, analysierte Wolfgang Rindler (1960)^[13] die Hyperbelbewegung in einer gekrümmten Raumzeit und zeigte (1966)^[14] die Analogie zwischen hyperbolischen Koordinaten  (2d),  (2e) in der flachen Raumzeit mit Kruskal-Koordinaten in der gekrümmten Raumzeit. Das beeinflusse nachfolgende Autoren bei ihrer Untersuchung der Unruh-Strahlung eines Beobachters in Hyperbelbewegung, die ähnlich ist zur Beschreibung der Hawking-Strahlung von Schwarzen Löchern.

Horizont

Born (1909) zeigte, dass die inneren Punkte eines Born-starren Körpers in Hyperbelbewegung nur in der Region ${\displaystyle X/\left(X^{2}-T^{2}\right)>0}$ sein können.^{[H 26]} Sommerfeld (1910) definierte den erlaubten Bereich für die hyperbolischen Koordinaten mit ${\displaystyle T<X}$.^{[H 27]} Kottler (1914)^{[H 28]} definierte den Bereich mit ${\displaystyle X^{2}-T^{2}>0}$ und erkannte die Existenz einer Grenzebene ${\displaystyle c^{2}/\alpha +x}$, hinter der kein Lichtsignal den Beobachter in Hyperbelbewegung erreichen kann. Bollert (1922)^{[H 29]} bezeichnete dies als den „Horizont des Beobachters“. Schließlich demonstrierte Rindler (1966)^[14] den Zusammenhang dieses Horizonts mit dem Horizont in Kruskal-Koordinaten.

Radar-Koordinaten

Unter Benutzung von Bollerts Formalismus fällte Stjepan Mohorovičić (1922)^{[H 30]} eine unterschiedliche Entscheidung für einige Parameter und erhielt die Metrik  (2h) mit einem Druckfehler, was von Bollert (1922b) korrigiert wurde mit einem anderen Druckfehler, bis Mohorovičić (1923) die Formel ohne Druckfehler angab. Mohorovičić war irrigerweise der Meinung, dass die Kottler-Møller-Metrik  (2b) falsch sei, was von Bollert (1922) zurückgewiesen wurde.^{[H 31]} Die Metrik  (2h) wurde von Harry Lass (1963) wiederentdeckt,^[12] der auch die entsprechenden Koordinaten  (2g) angab, weswegen sie manchmal als „Lass-Koordinaten“ bezeichnet werden.^[8] Die Metrik  (2h) als auch  (2a),  (2b) wurde auch von Fritz Rohrlich (1963) hergeleitet.^[11] Schließlich wurden die Lass-Koordinaten  (2g),  (2h) durch Desloge & Philpott (1987) mit Radar-Koordinaten identifiziert.^[40][36]

Tabelle mit historischen Formeln

Einzelnachweise

1. ↑ ^{a b c} Misner, C. W.; Thorne, K. S.; Wheeler, J. A.: Gravitation. Freeman, 1973, ISBN 0-7167-0344-0. 
2. ↑ ^{a b} Kopeikin, S., Efroimsky, M., Kaplan, G.: Relativistic Celestial Mechanics of the Solar System. John Wiley & Sons, 2011, ISBN 3-527-40856-8. 
3. ↑ Padmanabhan, T.: Gravitation: Foundations and Frontiers. Cambridge University Press, 2010, ISBN 1-139-48539-3. 
4. ↑ N. D. Birrell, P. C. W. Davies: Quantum Fields in Curved Space. Cambridge Monographs on Mathematical Physics Auflage. Cambridge University Press, 1982, ISBN 1-107-39281-0. 
5. ↑ Leonard Susskind, James Lindesay: An Introduction to Black Holes, Information and the String Theory Revolution: The Holographic Universe. World Scientific, 2005, ISBN 981-256-131-5, S. 8–10. 
6. ↑ Øyvind Grøn: Lecture Notes on the General Theory of Relativity. Lecture Notes in Physics Auflage. Band 772. Springer, 2010, ISBN 0-387-88134-4, S. 86–91. 
7. ↑ Muñoz, Gerardo; Jones, Preston: The equivalence principle, uniformly accelerated reference frames, and the uniform gravitational field. In: American Journal of Physics. 78. Jahrgang, Nr. 4, 2010, S. 377–383, doi:10.1119/1.3272719, arxiv:1003.3022, bibcode:2010AmJPh..78..377M. 
8. ↑ ^{a b c} David Tilbrook: General Coordinatisations of the Flat Space-Time of Constant Proper-acceleration. In: Australian Journal of Physics. 50. Jahrgang, Nr. 5, 1997, S. 851–868, doi:10.1071/P96111. 
9. ↑ Jones, Preston; Wanex, Lucas F.: The Clock Paradox in a Static Homogeneous Gravitational Field. In: Foundations of Physics Letters. 19. Jahrgang, Nr. 1, 2006, S. 75–85, doi:10.1007/s10702-006-1850-3, arxiv:physics/0604025, bibcode:2006FoPhL..19...75J. 
10. ↑ Birrill & Davies (1982), pp. 110–111 oder Padmanabhan (2010), p. 126 bezeichnen  (2g),  (2h) als Rindler-Koordinaten; Tilbrook (1997) pp. 864-864 oder Jones & Wanex (2006) bezeichnen  (2a),  (2b) ebenfalls als Rindler-Koordinaten
11. ↑ ^{a b c d} Rohrlich, Fritz: The principle of equivalence. In: Annals of Physics. 22. Jahrgang, Nr. 2, 1963, S. 169–191, doi:10.1016/0003-4916(63)90051-4, bibcode:1963AnPhy..22..169R. 
12. ↑ ^{a b} Harry Lass: Accelerating Frames of Reference and the Clock Paradox. In: American Journal of Physics. 31. Jahrgang, Nr. 4, 1963, S. 274–276, doi:10.1119/1.1969430, bibcode:1963AmJPh..31..274L. 
13. ↑ ^{a b} Rindler, W.: Hyperbolic Motion in Curved Space Time. In: Physical Review. 119. Jahrgang, Nr. 6, 1960, S. 2082–2089, doi:10.1103/PhysRev.119.2082, bibcode:1960PhRv..119.2082R. 
14. ↑ ^{a b c} Rindler, W.: Kruskal Space and the Uniformly Accelerated Frame. In: American Journal of Physics. 34. Jahrgang, Nr. 12, 1966, S. 1174–1178, doi:10.1119/1.1972547, bibcode:1966AmJPh..34.1174R. 
15. ↑ von Laue, M.: Die Relativitätstheorie, Band 1. Vierte Ausgabe von "Das Relativitätsprinzip” Auflage. Vieweg, 1921 (Online). ; Erste Ausgabe 1911, zweite 1913, dritte 1919.
16. ↑ ^{a b} Pauli, Wolfgang: Die Relativitätstheorie. In: Encyclopädie der mathematischen Wissenschaften. 5. Jahrgang, Nr. 2, 1921, S. 539–776 (uni-goettingen.de). 
17. ↑ ^{a b} Møller, C.: The theory of relativity. Oxford Clarendon Press, 1952 (Online). 
18. ↑ PhysicsFAQ (2016), „Relativistic rocket“, siehe Weblinks
19. ↑ Gallant, J.: Doing Physics with Scientific Notebook: A Problem Solving Approach. John Wiley & Sons, 2012, ISBN 0-470-66597-1, S. 437–441. 
20. ↑ Müller, T., King, A., & Adis, D.: A trip to the end of the universe and the twin "paradox". In: American Journal of Physics. 76. Jahrgang, Nr. 4, 2006, S. 360–373, doi:10.1119/1.2830528, arxiv:physics/0612126, bibcode:2008AmJPh..76..360M. 
21. ↑ ^{a b} Fraundorf, P.: A traveler-centered intro to kinematics. In: arxiv. 2012, S. IV–B, arxiv:1206.2877, bibcode:2012arXiv1206.2877F. 
22. ↑ Pauli (1921), p. 628
23. ↑ Galeriu, C.: Electric charge in hyperbolic motion: the early history. In: Archive for History of Exact Sciences. 71. Jahrgang, Nr. 4, S. 1–16, doi:10.1007/s00407-017-0191-x, arxiv:1509.02504.  Fehler beim Aufruf der Vorlage:cite journal: Parameter 'day', 'month', 'year' oder 'date', hat ungültigen Wert.
24. ↑ ^{a b} Bondi, H., & Gold, T.: The field of a uniformly accelerated charge, with special reference to the problem of gravitational acceleration. In: Proceedings of the Royal Society of London. 229. Jahrgang, Nr. 1178, 1955, S. 416–424, doi:10.1098/rspa.1955.0098, bibcode:1955RSPSA.229..416B. 
25. ↑ ^{a b} Fulton, Thomas; Rohrlich, Fritz: Classical radiation from a uniformly accelerated charge. In: Annals of Physics. 9. Jahrgang, Nr. 4, 1960, S. 499–517, doi:10.1016/0003-4916(60)90105-6, bibcode:1960AnPhy...9..499F. 
26. ↑ Stephen Lyle: Uniformly Accelerating Charged Particles: A Threat to the Equivalence Principle. Springer, 2008, ISBN 3-540-68477-8. 
27. ↑ Øyvind Grøn: Review Article: Electrodynamics of Radiating Charges. In: Advances in Mathematical Physics. 2012. Jahrgang, 2012, S. 528631, doi:10.1155/2012/528631. 
28. ↑ Møller (1952), eq. 154
29. ↑ Misner & Thorne & Wheeler (1973), section 6.6
30. ↑ Muñoz & Jones (2010), eq. 37, 38
31. ↑ Pauli (1921), section 32-y
32. ↑ Rindler (1966), p. 1177
33. ↑ Don Koks: Explorations in Mathematical Physics. Springer, 2006, ISBN 0-387-30943-8, S. 235–269. 
34. ↑ Massimo Pauri, Michele Vallisneri: Märzke-Wheeler coordinates for accelerated observers in special relativity. In: Foundations of Physics Letters. 13. Jahrgang, Nr. 5, 2000, S. 401–425, doi:10.1023/A:1007861914639, arxiv:gr-qc/0006095. 
35. ↑ Dolby, Carl E.; Gull, Stephen F.: On radar time and the twin "paradox". In: American Journal of Physics. 69. Jahrgang, Nr. 12, 2001, S. 1257–1261, doi:10.1119/1.1407254, arxiv:gr-qc/0104077, bibcode:2001AmJPh..69.1257D. 
36. ↑ ^{a b} Minguzzi, E.: The Minkowski metric in non-inertial observer radar coordinates. In: American Journal of Physics. 73. Jahrgang, 2005, S. 1117–1121, doi:10.1119/1.2060716, arxiv:physics/0412024, bibcode:2005AmJPh..73.1117M. 
37. ↑ ^{a b} Kastrup, H. A.: On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics. In: Annalen der Physik. 520. Jahrgang, Nr. 9–10, 2008, S. 631–690, doi:10.1002/andp.200810324, arxiv:0808.2730, bibcode:2008AnP...520..631K. 
38. ↑ ^{a b} Fulton, T., Rohrlich, F., & Witten, L.: Physical consequences of a co-ordinate transformation to a uniformly accelerating frame. In: Il Nuovo Cimento. 26. Jahrgang, Nr. 4, 1962, S. 652–671, doi:10.1007/BF02781794, bibcode:1962NCim...26..652F. 
39. ↑ Blum, A. S., Renn, J., Salisbury, D. C., Schemmel, M., & Sundermeyer, K.: 1912: A turning point on Einstein's way to general relativity. In: Annalen der Physik. 524. Jahrgang, Nr. 1, 2012, S. A12-A13, doi:10.1002/andp.201100705, bibcode:2012AnP...524A..11B. 
40. ↑ Desloge, Edward A.; Philpott, R. J.: Uniformly accelerated reference frames in special relativity. In: American Journal of Physics. 55. Jahrgang, Nr. 3, 1987, S. 252–261, doi:10.1119/1.15197, bibcode:1987AmJPh..55..252D. 
41. ↑ Herglotz (1909), pp. 408, 414

Historische Quellen

1. ↑ ^{a b} Einstein, Albert: Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. In: Jahrbuch der Radioaktivität und Elektronik. 4. Jahrgang, S. 411–462, bibcode:1908JRE.....4..411E (soso.ch [PDF]).  Fehler beim Aufruf der Vorlage:cite journal: Parameter 'day', 'month', 'year' oder 'date', hat ungültigen Wert. Einstein, Albert: Lichtgeschwindigkeit und Statik des Gravitationsfeldes. In: Annalen der Physik. 343. Jahrgang, Nr. 343, 1912, S. 355–369. 
2. ↑ ^{a b} Born, Max: Die Theorie des starren Elektrons in der Kinematik des Relativitätsprinzips. In: Annalen der Physik. 335. Jahrgang, Nr. 11, 1909, S. 1–56, doi:10.1002/andp.19093351102, bibcode:1909AnP...335....1B. 
3. ↑ ^{a b c} Herglotz, Gustav: Über den vom Standpunkt des Relativitätsprinzips aus als starr zu bezeichnenden Körper. In: Annalen der Physik. 336. Jahrgang, Nr. 2, S. 393–415, doi:10.1002/andp.19103360208, bibcode:1910AnP...336..393H.  Fehler beim Aufruf der Vorlage:cite journal: Parameter 'day', 'month', 'year' oder 'date', hat ungültigen Wert.
4. ↑ ^{a b c d e} Sommerfeld, Arnold: Zur Relativitätstheorie II: Vierdimensionale Vektoranalysis. In: Annalen der Physik. 338. Jahrgang, Nr. 14, 1910, S. 649–689, doi:10.1002/andp.19103381402, bibcode:1910AnP...338..649S. 
5. ↑ ^{a b c} Laue, Max von: Das Relativitätsprinzip. Vieweg, Braunschweig 1911 (Online). 
6. ↑ Lorentz, Hendrik Antoon: Das Relativitätsprinzip. Drei Vorlesungen gehalten in Teylers Stiftung zu Haarlem (1913). B.G. Teubner, Leipzig/Berlin 1913. 
7. ↑ Kottler, Friedrich: Über die Raumzeitlinien der Minkowski'schen Welt. In: Wiener Sitzungsberichte 2a. 121. Jahrgang, 1912, S. 1659–1759 (hathitrust.org).  Kottler, Friedrich: Relativitätsprinzip und beschleunigte Bewegung. In: Annalen der Physik. 349. Jahrgang, Nr. 13, 1914, S. 701–748, doi:10.1002/andp.19143491303, bibcode:1914AnP...349..701K (bnf.fr).  Kottler, Friedrich: Fallende Bezugssysteme vom Standpunkte des Relativitätsprinzips. In: Annalen der Physik. 350. Jahrgang, Nr. 20, 1914, S. 481–516, doi:10.1002/andp.19143502003, bibcode:1914AnP...350..481K (bnf.fr).  Kottler, Friedrich: Über Einsteins Äquivalenzhypothese und die Gravitation. In: Annalen der Physik. 355. Jahrgang, Nr. 16, 1916, S. 955–972, doi:10.1002/andp.19163551605, bibcode:1916AnP...355..955K (bnf.fr).  Kottler, Friedrich: Über die physikalischen Grundlagen der Einsteinschen Relativitätstheorie. In: Annalen der Physik. 361. Jahrgang, Nr. 14, 1918, S. 401–461, doi:10.1002/andp.19183611402, bibcode:1918AnP...361..401K (bnf.fr). 
8. ↑ ^{a b} Pauli, W.: Encyclopädie der mathematischen Wissenschaften. Band 5.2, 1921, Die Relativitätstheorie, S. 539–776.  New edition 2013: Editor: Domenico Giulini, Springer, 2013, ISBN 3-642-58355-5.
9. ↑ Karl Bollert: Das homogene Gravitationsfeld und die Lorentztransformationen. In: Zeitschrift für Physik. 10. Jahrgang, Nr. 1, 1922, S. 256–266, doi:10.1007/BF01332567, bibcode:1922ZPhy...10..256B.  Karl Bollert: Die Entstehung der Lorentzverkürzung und die strenge Behandlung des Uhrenparadoxons. In: Zeitschrift für Physik. 12. Jahrgang, Nr. 1, 1922, S. 189–206, doi:10.1007/BF01328090, bibcode:1923ZPhy...12..189B. 
10. ↑ Mohorovičić, S.: Das „homogene“ Gravitationsfeld und die Lorentztransformation. In: Zeitschrift für Physik. 11. Jahrgang, Nr. 1, 1922, S. 88–92, doi:10.1007/BF01328404, bibcode:1922ZPhy...11...88M.  Mohorovičić, S.: Äther, Materie, Gravitation und Relativitätstheorie. In: Zeitschrift für Physik. 18. Jahrgang, Nr. 1, 1923, S. 34–63, doi:10.1007/BF01327684, bibcode:1923ZPhy...18...34M. 
11. ↑ Lemaître, G.: The motion of a rigid solid according to the relativity principle. In: Philosophical Magazine Series 6. 48. Jahrgang, Nr. 283, 1924, S. 164–176, doi:10.1080/14786442408634478. 
12. ↑ ^{a b} Møller, C.: On homogeneous gravitational fields in the general theory of relativity and the clock paradox. In: Dan. Mat. Fys. Medd. 8. Jahrgang, 1943, S. 3–25.  Møller, C.: The theory of relativity. Oxford Clarendon Press, 1952 (Online). 
13. ↑ Sommerfeld (1910), pp. 670–671.
14. ↑ Kottler (1914b), pp. 488–489, 492–493
15. ↑ Minkowski, Hermann: Raum und Zeit. Vortrag, gehalten auf der 80. Naturforscher-Versammlung zu Köln am 21. September 1908. In: Jahresbericht der Deutschen Mathematiker-Vereinigung. Leipzig 1909. 
16. ↑ Einstein, Albert & Rosen, Nathan: A Particle Problem in the General Theory of Relativity. In: Physical Review. 48. Jahrgang, 1935, S. 73, doi:10.1103/PhysRev.48.73, bibcode:1935PhRv...48...73E. 
17. ↑ ^{a b} Born (1909), p. 25
18. ↑ ^{a b} Sommerfeld (1910), pp. 670–671
19. ↑ ^{a b} Einstein (1912), pp. 358–359
20. ↑ ^{a b} Lorentz (1913), pp. 34–38; 50–52
21. ↑ Kottler (1912), pp. 1715; Kottler (1914a), Table I; pp. 747–748; Kottler (1914b), pp. 488–489, 503; Kottler (1916), pp. 958–959; (1918), pp. 453–454;
22. ↑ ^{a b} Bollert (1922a), p. 261, 266
23. ↑ ^{a b} Lemaitre (1921), pp. 166, 168
24. ↑ ^{a b} Einstein & Rosen (1935), p. 74
25. ↑ ^{a b} Møller (1952), pp. 121–123; 255–258
26. ↑ Born (1909), p. 35
27. ↑ Sommerfeld (1910), p. 672
28. ↑ Kottler (1914), pp. 489–490
29. ↑ Bollert (1922b), pp. 194–196
30. ↑ ^{a b} Mohorovičić (1922), p. 92, ohne ${\displaystyle x_{1}}$ im Exponenten durch Druckfehler, korrigiert durch Bollert (1922b), p. 189 und vollständig durch Mohorovičić (1923), p. 54
31. ↑ Bollert (1922b), p. 189
32. ↑ Einstein (1907), §§ 18–21
33. ↑ von Laue (1911), p. 109
34. ↑ Kottler (1912), pp. 1715
35. ↑ Kottler (1914a), Table I; pp. 747–748
36. ↑ Kottler (1914b), pp. 488–489, 503
37. ↑ Kottler (1916), pp. 958–959; (1918), pp. 453–454
38. ↑ Pauli (1921), pp. 647–648

Weblinks

Commons: Rindler Chart – Sammlung von Bildern, Videos und Audiodateien

• Physics FAQ: The Relativistic Rocket
• Mathpages: Accelerated Travels, Does A Uniformly Accelerating Charge Radiate?