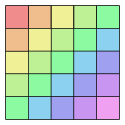
Hankel-Matrix

Besetzungsmuster einer Hankel-Matrix der Größe 5×5

Eine Hankel-Matrix, benannt nach Hermann Hankel (1839–1873), bezeichnet eine quadratische Matrix, bei der auf jeder von rechts oben nach links unten verlaufenden Gegendiagonalen jeweils nur ein konstanter Wert auftritt.^[1] Sie ist also durch die oberste Zeile und die äußerste rechte Spalte der Matrix vollständig beschrieben.

Eine Hankel-Matrix ist eine symmetrische Matrix. Die Dimension des Vektorraums der ${\displaystyle n\times n}$ Hankel-Matrizen ist ${\displaystyle 2n-1}$.

Diese Vereinfachung erlaubt ebenso wie bei den verwandten Toeplitz-Matrizen den Einsatz besonders effizienter Verfahren für Matrixoperationen wie Multiplikation und Inversion.

Beispiel

Hier ein Beispiel einer ${\displaystyle 4\times 4}$-Hankel-Matrix:

${\displaystyle M={\begin{pmatrix}1&2&3&4\\2&3&4&5\\3&4&5&6\\4&5&6&7\\\end{pmatrix}}}$

Ein sehr bekanntes Beispiel einer Hankel-Matrix ist die Hilbert-Matrix.

Einzelnachweise

1. ↑ Hankel-Matrix. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8 (google.de).