Grenzorbital



Als Grenzorbitale werden im Rahmen der Molekülorbitaltheorie das höchste besetzte und das niedrigste unbesetzte Molekülorbital zusammen bezeichnet.[1] Mittels der Grenzorbitaltheorie lassen sich verschiedene Konzepte der Chemie, z. B. die Reaktivität von Molekülen, qualitativ verstehen.[2] Als Begründer der Grenzorbitaltheorie gilt der Chemienobelpreisträger Kenichi Fukui.
HOMO
Highest Occupied Molecular Orbital (HOMO, engl.) bezeichnet das höchste besetzte Orbital eines Moleküls.
In einem Molekül stehen verschiedene Molekülorbitale zur Verfügung, die von den vorhandenen Elektronen besetzt werden. Diese Orbitale weisen verschiedene Orbitalenergien auf. Sie werden nach zunehmendem Energieniveau besetzt. Das HOMO ist das energiereichste besetzte Orbital.
LUMO
Lowest Unoccupied Molecular Orbital (LUMO) bezeichnet auf Englisch das niedrigste unbesetzte Orbital eines Moleküls.
Die energetische Höhe des LUMOs wird auch als Maß für die Elektrophilie verwendet.
HOMO und LUMO Energien in der Anwendung
Bedeutsam ist der Energieunterschied zwischen dem HOMO und dem LUMO, in der Halbleiterforschung als Band Gap bezeichnet wird. Vom Betrag dieses Energieunterschiedes hängt es nämlich näherungsweise ab, wie leicht die Elektronen vom Grundzustand in den angeregten Zustand erreichen.[3][4]
In organischen Solarzellen erreicht man durch die Kombination verschiedener Materialien[5] mit unterschiedlichen Energiedifferenzen zwischen HOMO und LUMO (Heteroübergang), dass die durch das eingestrahlte Licht angeregten Zustände (Exzitonen) besser aufgespalten werden können. Eine solche Aufspaltung ist nötig, um freie Ladungsträger und somit Strom aus den Solarzellen gewinnen zu können.
Siehe auch
Einzelnachweise
- ↑ Ian Fleming: Molecular Orbitals and Organic Chemical Reactions. John Wiley & Sons, 24. August 2011, S. 215 ff.
- ↑ Frank Jensen: Introduction to Computational Chemistry. Wiley, 2007, ISBN 978-0-470-05804-6, S. 487 ff.
- ↑ Peter Atkins: Physikalische Chemie. Hrsg.: Wiley-VCH. 5. Auflage. John Wiley & Sons, 2013.
- ↑ Die Differenz der Grenzorbitalenergien stellt eine grobe Näherung für die Anregungsenergie dar. Zieht man z. B. die Anregungsenergie im Formalismus der Configuration Interaction heran (z. B. CIS), so sieht man, dass die Orbitalenergiedifferenzen eine wichtige Rolle spielen. Allerdings vernachlässigt diese Näherung die (durch die Anregung) veränderten Elektron-Elektron-Wechselwirkungen:
- ↑ von D. Dick, TU Kaiserslautern ( vom 14. Juli 2014 im Internet Archive)
Auf dieser Seite verwendete Medien
Autor/Urheber: FD, Lizenz: CC BY-SA 4.0
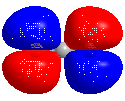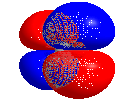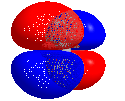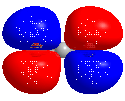
Three dimensional rotating model of CO2, showing its HOMO. Minimum energy conformation calculated using Gaussian 09 (DFT, 6-311G), molecular model created using Chem3D 16.0.
Diagram of HOMO and LUMO molecular orbitals.
Autor/Urheber: FD, Lizenz: CC BY-SA 4.0
Three dimensional rotating model of CO2, showing its LUMO. Minimum energy conformation calculated using Gaussian 09 (DFT, 6-311G), molecular model created using Chem3D 16.0.