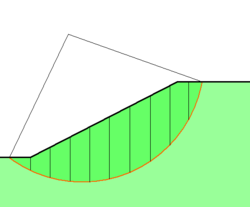
Gleitkreisverfahren

Das Gleitkreisverfahren (englisch: Method of Slices und general limit equilibrium method) ist eine Methode zur Berechnung der Standsicherheit von Böschungen in der Geotechnik (Nachweis gegen Böschungsbruch).
Beschreibung


Da beim Abrutschen einer Böschung häufig kreisbogenförmige Rutschflächen entstehen (besonders deutlich in Ton, wo Alexandre Collin dies in den 1840er Jahren zuerst beobachtete), untersucht man kreisförmige Bruchkörper und spricht deshalb vom Gleitkreisverfahren.
Bei der Berechnung unterscheidet man (s. u.):
- lamellenfreie Verfahren (hierbei gibt es einen einzigen Bruchkörper)
- Lamellenverfahren (hierbei wird der Bruchkörper in viele vertikale Scheiben, die Lamellen, unterteilt).
Die Verfahren unterteilen sich weiter nach
- den Kräften (Eigengewicht, Erddruck, Wasserdruck, Auftrieb, Verkehrslast usw.)
- den Widerständen (Reibung, Scherfestigkeit)
- den Mechanismen, die dabei berücksichtigt bzw. vernachlässigt werden.
Bei einem konkreten Standsicherheitsnachweis einer Böschung variiert man den Mittelpunkt und den Radius der Gleitkreise schrittweise solange, bis man den Kreisbogen mit der niedrigsten und damit maßgebenden Sicherheit gefunden hat.
Lamellenfreies Verfahren
Beim lamellenfreien Verfahren wird der Bruchkörper so betrachtet, als ob er als Ganzes auf einer kreisbogenförmigen Fläche abrutscht. Alle angreifenden äußeren Kräfte werden zu einer resultierenden Kraft zusammengefasst und mit den widerstehenden Kräften in der Gleitfuge verglichen. Die Standsicherheit wird nach Fellenius für den ermittelten Gleitkreis bestimmt aus dem Verhältnis der widerstehenden Kräfte zu den angreifenden Kräften und der Drehmomente um den Kreismittelpunkt.
Lamellenverfahren
Beim Lamellenverfahren nach Krey/Bishop teilt man den Bruchkörper in mehrere senkrechte Lamellen, auf die die verschiedenen Kräfte einwirken. An jeder Lamelle formuliert man das Kräftegleichgewicht. Hierbei gibt es neben den oben genannten Kräften zusätzlich Erddruckkräfte an den beiden Seiten der Lamellen. Die Kräfte der Lamellen summiert man zum Gesamtgleichgewicht auf.
Geschichte
Die ersten, die Berechnungen nach dem Gleitkreisverfahren durchführten, waren Knut Petterson und Sven Hultin von der Hafenbehörde in Göteborg im Jahr 1916.[1][2] Sie berechneten die Rutschung einer Hafenkaimauer.[3] Fellenius[4] (und auch Krey[5]) verbesserten das Verfahren in den 1920er Jahren so weit, dass es heute eher unter dem Namen Fellenius-Verfahren oder auch als Krey-Bishop-Verfahren bekannt ist. Verschiedene Autoren haben später (in den 1950ern und danach) Beiträge und Verbesserungen geliefert (Otto Karl Fröhlich[6], Alan W. Bishop[7], Nilmar Janbu[8], Hubert Borowicka[9] usw.).
Alternativen
Neben den Gleitkreisverfahren gibt es auch Verfahren mit polygonartigen Gleitflächen, z. B. nach Janbu. Auch Morgenstern/Price haben eine Methode zur Böschungsbruchberechnung beschrieben (Lamellenmethode, nicht kreisförmige Bruchflächen, keine Rotation, Gleichgewicht exakt erfüllt).[10]
Heute findet man Richtlinien für Gelände- und Böschungsbruch-Berechnungen nach diesen Methoden in der DIN 4084.
Ein alternatives Verfahren für die Berechnung von Böschungen ist die Kinematische-Elemente-Methode.
Literatur
- Konrad Simmer, Grundbau, Band 1, Kapitel 6.4 (Gelände- und Böschungsbruch), 19. Auflage, Teubner 1994, S. 211–232
Einzelnachweise
- ↑ SWEDISH GEOTECHNICAL SOCIETY ( des vom 9. Oktober 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis. sowie K. E. Petterson The early history of circular sliding surfaces, Geotechnique, Band 5, 1955, S. 275–296
- ↑ Historische Talsperren, Garbrecht 1987
- ↑ Karl-Eugen Kurrer The History of the Theory of Structures. Searching for Equilibrium, Ernst & Sohn, Berlin 2018, S. 341ff
- ↑ Fellenius Erdstatische Berechnungen mit Reibung und Kohäsion, Ernst und Sohn, Berlin 1927, Fellenius Calculation of the Stability of Earth Dams, Transactions Second Congress on Large Dams, Washington D.C., 1936, Band 4, S. 445
- ↑ Krey: Erddruck, Erdwiderstand und Tragfähigkeit des Baugrundes, 5. Auflage, 1936, Ernst und Sohn, Berlin
- ↑ Fröhlich General Theory of Stability of Slopes, Geotechnique, Band 5, 1955, S. 37, Grundzüge einer Statik der Erdböschungen, Der Bauingenieur 1963, Heft 10
- ↑ Bishop Use of the slip circle in the stability analysis of slopes, Geotechnique, Band 5, 1955, S. 7
- ↑ Janbu Stability analysis of slopes with dimensionless parameters, Harvard Soil Mechanics Series Nr. 46, 1954
- ↑ Borowicka Die Standsicherheit der Böschung in Theorie und Praxis, Bauingenieur, Band 40, 1965, S. 21, Ein statisch einwandfreies Verfahren zur Ermittlung der Standsicherheit von Böschungen, Der Bauingenieur 1970, Heft 9
- ↑ Morgenstern/Price, GEOTECHNIQUE. VOL. 15,' NO.1, 1965: The analysis of the stability of general slip surfaces. Abgerufen am 27. Januar 2018.
Weblinks
- TUM: Lehrstuhl für Grundbau, Bodenmechanik, Felsmechanik und Tunnelbau: Böschungen und Geländesprünge ( vom 18. Juli 2013 im Internet Archive) (PDF-Datei; 1,3 MB)
- TUM: Lehrstuhl für Grundbau, Bodenmechanik, Felsmechanik und Tunnelbau: Böschungsstabilität (PDF-Datei; 539 kB)
- METHOD OF SLICES
- ORDINARY METHOD OF SLICES (FELLENIUS METHOD) (PDF-Datei; 60 kB)
Auf dieser Seite verwendete Medien
Autor/Urheber: ProfessorX, Lizenz: CC BY-SA 3.0
Böschungsbruch, Erdrutsch an einer Böschung
Gleitkreis-Bruchkörper beim Gleitkreisverfahren (Böschungsbruch)