Gleichschenkliges Dreieck

Ein gleichschenkliges Dreieck ist ein Dreieck mit mindestens zwei gleich langen Seiten. Folglich sind auch die beiden Winkel gleich groß, die den gleich langen Seiten gegenüberliegen. Zur vollständigen Bestimmung werden zwei Bestimmungsstücke benötigt, davon zumindest eine Seite.
Die beiden gleich langen Seiten heißen Schenkel, die dritte Seite heißt Basis. Der der Basis gegenüberliegende Eckpunkt heißt Spitze. Die an der Basis anliegenden Winkel heißen Basiswinkel.
Jedes gleichschenklige Dreieck ist achsensymmetrisch. Es kann spitzwinklig, rechtwinklig oder stumpfwinklig sein. Schließt die Spitze den Winkel oder ein, wird es Goldenes Dreieck erster bzw. zweiter Art genannt.
Berechnung und Konstruktion
| Mathematische Formeln zum gleichschenkligen Dreieck | ||
|---|---|---|
| Flächeninhalt | ||
| Umfang | ||
| Seitenlängen | ||
| Winkel | ||
| Höhe[1] | ||
| Inkreisradius[1] | ||
| Umkreisradius | ||
Basiswinkelsatz
Der Basiswinkelsatz besagt, dass in einem gleichschenkligen Dreieck die beiden Basiswinkel, also die Winkel, die den gleich langen Seiten gegenüberliegen, gleich groß sind. Umgekehrt gilt auch: Sind in einem Dreieck zwei Winkel gleich groß, so sind auch die beiden gegenüberliegenden Seiten gleich lang.
Zwei Seiten
Im gleichschenkligen Dreieck ist bei gegebenen zwei Seiten das Dreieck nur dann bestimmt, wenn eine der gegebenen Seiten weniger als halb so lang wie die andere. In diesem Fall ist die kurze Seite wegen der Dreiecksungleichung immer die Basis. Dadurch ergibt sich dann indirekt eine Bestimmtheit durch drei gegebene Seiten. Die Winkel können mit Hilfe des Kosinussatzes berechnet werden.
Eine Seite und ein Winkel
Ist ein Winkel gegeben, so lassen sich aus der Beziehung
sofort alle übrigen Winkel berechnen. Dadurch kann man das Dreieck nach dem WSW-Fall behandeln. Die fehlenden Seiten können mit dem Sinussatz berechnet werden.
Ausgezeichnete Punkte
Gleichschenklige Dreiecke sind achsensymmetrisch. Die Symmetrieachse stimmt mit der Höhe, der Mittelsenkrechten (Streckensymmetrale) und der Seitenhalbierenden (Schwerlinie) der Basis und mit der Winkelhalbierenden (Winkelsymmetrale) des Winkels an der Spitze überein. Der Höhenschnittpunkt, der Umkreismittelpunkt, der Schwerpunkt und der Inkreismittelpunkt liegen auf dieser Symmetrieachse.
In einem gleichschenkligen Dreieck, das nicht gleichseitig ist, stimmt die eulersche Gerade also mit der Symmetrieachse überein.
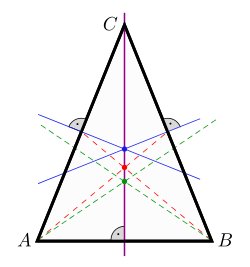 | Gleichschenkliges Dreieck mit
|
Siehe auch: Ausgezeichnete Punkte im Dreieck
Sehnenvielecke

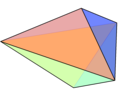
Jedes Sehnenvieleck, das den Mittelpunkt seines Umkreises enthält, kann von den Radien dieses Kreises, die durch seine Eckpunkte verlaufen, in gleichschenklige Dreiecke unterteilt werden. Diese Dreiecke sind gleichschenklig, weil alle Radien eines Kreises gleich lang sind. Diese Zerlegung kann verwendet werden, um eine Formel für den Flächeninhalt des Polygons als Funktion seiner Seitenlängen abzuleiten, auch für Sehnenvielecke, die ihren Umkreismittelpunkt nicht enthalten. Diese Formel verallgemeinert den Satz des Heron für Dreiecke und Brahmaguptas Formel für Sehnenvierecke.
Polyeder mit gleichschenkligen Dreiecken
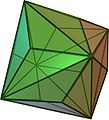
Einige besondere Polyeder haben gleichschenklige Dreiecke als Seitenflächen, zum Beispiel regelmäßige Pyramiden und regelmäßige Doppelpyramiden. Die Oberfläche einiger catalanischer Körper besteht aus kongruenten gleichschenkligen Dreiecken. Die genannten Polyeder sind drehsymmetrisch, d. h. sie können durch Drehung um bestimmte Rotationsachsen auf sich selbst abgebildet werden.
- Quadratische Pyramide
- Regelmäßige fünfseitige Pyramide
- Dreiseitige regelmäßige Doppelpyramide
- Quadratische Doppelpyramide
- (c) Cyp, CC BY-SA 3.0
Siehe auch
- Dreieck
- Gleichseitiges Dreieck
- Rechtwinkliges Dreieck
- Spitzwinkliges Dreieck
- Stumpfwinkliges Dreieck
- Schenkeltransversalensatz (Lehrsatz über gleichschenklige Dreiecke)
Literatur
- H. S. M. Coxeter: Unvergängliche Geometrie. Birkhäuser, Basel [u. a.] 1963 (Deutsche Übersetzung von: Introduction to Geometry. Wiley, 1961).
Weblinks
- Eric W. Weisstein: Isosceles Triangle. In: MathWorld (englisch).
Einzelnachweise
- ↑ a b Jürgen Köller: Gleichschenkliges Dreieck. Höhe und Radius des Inkreises. Abgerufen am 8. Juni 2019.
Auf dieser Seite verwendete Medien
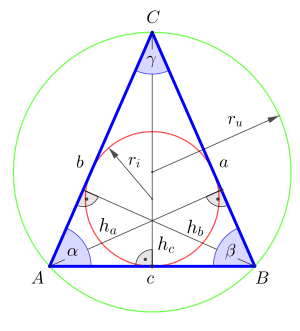
Autor/Urheber: MartinThoma, Lizenz: CC BY 3.0
Gleichschenkliges Dreieck mit
Autor/Urheber: David Eppstein, Lizenz: CC0
A cyclic polygon (in this case a pentagon) can be partitioned into isosceles triangles by the radii of its circumscribing circle through its vertices.
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Gleichschenkliges Dreieck mit dessen Größen
An SVG drawing of isosceles triangle, marked in the Russian textbook tradition