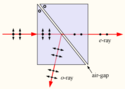
Glan-Taylor-Prisma
Das Glan-Taylor-Prisma (nach Paul Glan und A. M. Taylor) ist ein auf Doppelbrechung und Totalreflexion basierender Polarisator, der unpolarisiertes Licht linear polarisiert. Der Grundaufbau des Prismas entspricht dem 1880 von Paul Glan[1] vorgestellten Polarisationsprisma mit Einfallsflächen senkrecht zur optischen Achse (OA) des doppelbrechenden Kristalls (Glan-Prisma oder auch Glan-Foucault-Prisma bzw. namensgebend für den Typ auch Glan-Typ genannt) und 1948 von John Frederick Archard und A. M. Taylor[2] modifiziert (AO um 90° gedreht) und in bestimmten Eigenschaften verbessert wurde.
Aufbau
Das Glan-Taylor-Prisma besteht wie alle Polarisationsprismen aus einem doppelbrechenden Kristall (typischerweise Kalkspat), der so geschnitten und poliert wurde, dass die Stirnflächen (Eintritts- und Austrittsfläche) parallel zur optischen Achse liegen. Der so geschnittene Kristall wird anschließend diagonal in zwei Teile geschnitten. Der Schnittwinkel der beiden Prismenhälften ist dabei so gewählt, dass der Brechungsindexunterschied zwischen ordentlichem und außerordentlichem Strahl ein unterschiedliches Reflexionsverhalten an der Grenzfläche zum Luftspalt bewirkt (Totalreflexion und normale Reflexion/Transmission). Die beiden Hälften werden danach wieder zusammengesetzt, aber nicht direkt zusammengefügt, sondern ein Luftspalt (hinreichend dick um Transmission ins zweite Prisma durch verhinderte Totalreflexion minimal zu halten) zwischen den Prismenteilen liefert Grenzflächen zu einem optisch dünneren Medium.
Der genaue Schnittwinkel ist abhängig von genutzten doppelbrechenden Materials und der Wellenlänge der Anwendung. Im Fall eines optisch negativen doppelbrechenden Materials wie Kalkspat ist der Brechungsindex für den ordentlichen Strahl (no = 1,658 bei 589 nm, Natrium-D-Linie) größer als für den außerordentlichen Strahl (nao = 1,486). Der Schnittwinkel liegt dabei zwischen dem kritischen Winkel des ordentlichen (37,1°) und dem kritischen Winkel des außerordentlichen Strahls (42,3°). Die Grundform eines Prismas aus Kalkspat ist daher ein näherungsweise gleichseitiger Würfel und damit deutlich kürzer als Prismen von Nicol-Typ.
Funktionsweise
Im Folgenden wird die Funktionsweise des Prismas am Beispiel des üblicherweise genutzten negativ doppelbrechenden Materials Kalkspat bei einer Wellenlänge von 589 nm (Natrium-D-Linie) beschrieben. Eventuell angebende Werte können für andere Wellenlängen und Materialien abweichen bzw. die Strahlselektion sich bei positiv doppelbrechenden Materialien umkehren.
Beim Eintritt in ein Material wird der einfallende Lichtstrahl nach dem Snellius-Brechungsgesetz gebrochen. Aufgrund der anisotropen Brechungsindices von doppelbrechenden Materialien wird sich der einfallende Strahl je nach seiner Polarisierungsrichtung unterschiedlich verhalten. Man unterscheidet den ordentlichen (senkrecht zur optischen Achse des Kristalls polarisierten) und den außerordentlichen (parallel zur optischen Achse polarisierten) Strahl.
Beim Einfall schräg zur optischen Achse, beispielsweise beim Nicol-Prisma, werden diese Strahlen unterschiedlich stark gebrochen. Bei Prismen vom Glan-Typ sind die beiden Kalkspat-Prismen so geschliffen, dass die Schnittflächen des Kristalls parallel zur optischen Achse liegen. Auf diesem Weg wird verhindert, dass nach der Brechung des einfallenden Strahls der ordentliche und der außerordentliche Strahl unterschiedliche Brechungswinkel aufweist. Bei senkrechtem Einfall werden beide Strahlenanteile also nicht gebrochen und bewegen sich auf einem gemeinsam Weg im Kristall, wenn auch aufgrund der unterschiedlichen Brechungsindizes mit unterschiedlicher Geschwindigkeit. Ein weiterer Vorteil dieser Strahlführung ist, die Minimierung des Reflexionsgrad auf der Stirnfläche und damit einen besseren Transmissionsgrad als Nicol-Typ-Prismen. Es ist jedoch zu beachten, dass anders als bei Nicol-Typ in diesem Fall keine Einfallsebene festgelegt werden kann, wo durch die Begriffe senkrecht und parallel polarisiertes Licht nicht klar zugeordnet werden können. Die Zuordnung erfolgt daher über die Schnittebene bzw. den Einfall auf der Schnittfläche.
Nach dem Eintritt in das Prisma laufen der ordentliche und der außerordentliche Strahl weiter parallel zur Längsrichtung des Prismas auf die Schnittfläche zu. Wie im Abschnitt Aufbau beschrieben liegt der Schnittwinkel der beiden Prismenhälften so, dass aufgrund des Brechungsindexunterschieds der beiden Strahlen nur der ordentliche Strahl totalreflektiert wird. Der außerordentliche Strahl wird hingegen in das Zwischenmedium Luft und anschließend in das zweite Prisma gebrochen. Das zweite (in der Abbildung rechte) Prisma dient nur der Kompensation der Strahlablenkung.[3] Beim Austritt aus dem Prisma an der hinteren Stirnfläche (parallel zum einfallenden Strahl) liegt nur noch der linear polarisierte außerordentliche Strahl vor, dessen Polarisationsebene parallel zu optischen Achse des Kristalls liegt.
In der Regel kann für die verfügbaren Materialien (und genutzten Wellenlängen) der Schnittwinkel nicht so gewählt werden, dass der Einfallswinkel der beiden Strahlen auf die Schnittfläche gleich dem Brewster-Winkel des außerordentlichem Strahl (θB,ao = 33,9°) entspricht und trotzdem die Grundfunktion gewahrt bleibt. Daher entstehen zusätzliche Reflexionsverluste an den Grenzflächen zum Zwischenmedium, was die Transmissionseigenschaften vor allem für Laseranwendungen verschlechtert, sie sind aber immer noch deutlich besser als bei anderen Polarisationsprismen. Des Weiteren kann es in diesem Fall auch zu Störungen durch Interferenzeffekten in der Luftschicht kommen und sich negativ auf die Qualität der Linearpolarisation auswirken.
Abgrenzung zu anderen Prismenarten
Das ebenfalls sehr ähnlich aufgebaute Glan-Foucault-Prisma (entspricht eher einem Glan-Thompson-Prisma mit Luft als Zwischenmedium) nutzt Prismenteile mit einer um 90° gedrehten optischen Achse. Dadurch wird eine um 90° gedrehte Polarisation selektiert (auf die Schnittfläche bezogen: s-polarisiert). Im Vergleich dazu zeigt das Glan-Taylor-Prisma deutlich verbesserte Transmissioneigenschaften und die Intensität der Mehrfachreflexionen durch die Luftschicht ist auf unter 10 % reduziert.[4]
Das Lippich-Prisma (nach Ferdinand Franz Lippich (1838–1913)) hat die gleiche Ausrichtung der optischen Achse wie das Glan-Taylor-Prisma, verfügt aber über keinen Luftspalt, sondern die beiden Prismenteile wurden mit einem durchsichtigen Kleber aneinander gefügt. Damit ist die Reflexion des außerordentlichen Stahls nicht mehr durch dessen Grenzwinkel der Totalreflexion begrenzt und ein Lippich-Prisma weist, wie andere Nicht-Luft-Polarisationsprismen, einen höheren Akzeptanzwinkel auf. Der Kleber ist jedoch nachteilig für Anwendungen mit hohen Strahlungsleistungen wie Laseroptiken, da dieser sich erwärmt und ggf. zersetzt.
Zwei rückseitig hintereinander positionierte Glan-Taylor-Prismen wird auch Marple-Hess-Prisma genannt.
Einzelnachweise
- ↑ Paul Glan: Ueber einen Polarisator. In: Repertorium für Experimental-Physik, für Physikalische Technik, Mathematische und Astronomische Instrumentenkunde. Band 16, 1880, S. 570.
- ↑ J. F. Archard, A. M. Taylor: Improved Glan-Foucault Prism. In: Journal of Scientific Instruments. Band 25, Nr. 12, 1948, S. 407–409, doi:10.1088/0950-7671/25/12/304.
- ↑ Gerd Litfin (Hrsg.): Technische Optik in der Praxis. 3. Auflage, Springer, Berlin 2006, ISBN 3-540-21884-X, S. 58 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Michael Bass (Hrsg.): Handbook of Optics, Third Edition Volume I : Geometrical and Physical Optics, Polarized Light, Components and Instruments. McGraw-Hill Professional, 2009, ISBN 978-0-07-162925-6, S. 13.9–13.12.
Auf dieser Seite verwendete Medien
(c) DrBob aus der englischsprachigen Wikipedia, CC-BY-SA-3.0
A Glan-Foucault prism. By Bob Mellish.
Autor/Urheber:
- Glan-taylor.png: Bob Mellish
- Glan-Thompson_prism_DE.svg: Cepheiden
- derivative work: Cepheiden (talk)
Schematische Darstellung der Strahlwege in einem Glan-Taylor-Prisma.