Gewöhnliche Differentialgleichung

Eine gewöhnliche Differentialgleichung (oft abgekürzt mit GDGL oder ODE, englisch ordinary differential equation) ist eine Differentialgleichung, bei der zu einer gesuchten Funktion nur Ableitungen nach genau einer Variablen auftreten.

Viele physikalische, chemische und biologische Vorgänge in der Natur lassen sich mit solchen Gleichungen mathematisch beschreiben, z. B. der radioaktive Zerfall, Bewegungsvorgänge von Körpern, viele Arten von Schwingungsvorgängen oder das Wachstumsverhalten von Tier-Populationen. In naturwissenschaftlichen Modellen werden gewöhnliche Differentialgleichungen daher häufig eingesetzt, um solche Vorgänge zu analysieren, zu simulieren oder um Vorhersagen abgeben zu können. In vielen Fällen kann die Differentialgleichung nicht analytisch gelöst werden. Man ist daher auf numerische Verfahren angewiesen. Siehe Hauptartikel: Liste numerischer Verfahren#Numerik gewöhnlicher Differentialgleichungen.

Historisch gesehen wurden die ersten Differentialgleichungen verwendet, um die Bewegung von Objekten zu modellieren. Besonders hervorzuheben sind dabei die Gleichungen für die Bewegung mit konstanter Geschwindigkeit bzw. konstanter Beschleunigung. Im Jahr 1590 erkannte Galileo Galilei den Zusammenhang zwischen der Fallzeit eines Körpers und seiner Fallgeschwindigkeit sowie dem Fallweg und formulierte (noch) mit geometrischen Mitteln das Gesetz des freien Falles.

Als Isaac Newton auch Bewegungen mit Reibungen betrachtete, die zum Betrag oder zum Quadrat der Geschwindigkeit proportional sind, war er genötigt, die Differentialrechnung und den heute geläufigen Formalismus der Differentialgleichungen einzuführen.

Durch die exakte Formulierung des Grenzwertbegriffes, der Ableitung und des Integrals stellte schließlich Augustin-Louis Cauchy im 19. Jahrhundert die Theorie der gewöhnlichen Differentialgleichungen auf ein festes Fundament und machte sie somit vielen Wissenschaften zugänglich.

Das wissenschaftliche Interesse an Differentialgleichungen ist im Wesentlichen darin begründet, dass mit ihnen auf Grund vergleichsweise einfacher Beobachtungen und Experimente vollständige Modelle geschaffen werden können.

Nur wenige Typen von Differentialgleichungen lassen sich analytisch lösen. Trotzdem lassen sich qualitative Aussagen wie Stabilität, Periodizität oder Bifurkation auch dann treffen, wenn die Differentialgleichung nicht explizit gelöst werden kann. Eines der wichtigsten Hilfsmittel für skalare Differentialgleichungen sind Argumente mittels eines Vergleichssatzes.

Allgemein enthält eine Differenzialgleichung (DGL) außer der gesuchten Funktion z. B. ${\displaystyle y(t)}$ auch mindestens eine Ableitung der gesuchten Funktion. Die Notation einer DGL mit dem Differentialquotienten ${\displaystyle {\frac {dy}{dx}}}$ einer bestimmten Ordnung wird zur Vereinfachung nicht immer mit der unabhängigen Variablen ${\displaystyle x}$ oder bei zeitabhängigen Funktionen mit ${\displaystyle t}$ dargestellt, sondern z. B. als ${\displaystyle y'}$ oder ${\displaystyle {\dot {y}}}$ für eine Ableitung 1. Ordnung. Eine DGL ist linear, wenn die gesuchte Funktion y(x) und deren Ableitungen keine Winkelfunktionen, Logarithmen oder Wurzeln enthält.

(c) HeinrichKü in der Wikipedia auf Deutsch, CC BY-SA 3.0

Ein bekanntes Beispiel einer linearen GDGL mit konstanten Koeffizienten einer Verzögerungsfunktion 1. Ordnung (PT1-Glied) lautet in expliziter Darstellung:

${\displaystyle y'(t)={\frac {K_{PT1}\cdot u(t)-y(t)}{T_{1}}}}$. ${\displaystyle \qquad ({K_{PT1}\cdot u(t)}\ {\text{ist die Störfunktion}})}$

Bei dieser linearen inhomogenen DGL mit Störfunktion (${\displaystyle u(t)}$ = Eingangssprung) bedeutet ${\displaystyle T_{1}}$ die Zeitkonstante, und ${\displaystyle K_{PT1}}$ der Proportionalitätsfaktor.

Anmerkung: Bei der expliziten Darstellung der DGL werden sämtliche Koeffizienten der übrigen Ableitungen einschließlich Störfunktion durch den Koeffizienten der höchsten Ableitung dividiert.

Prinzipiell ist die Lösung ${\displaystyle y(x)}$ einer DGL eine Funktion mit einem kontinuierlichen Werteverlauf in Abhängigkeit von der unabhängigen Variable ${\displaystyle x}$. Eine DGL hat in der Regel unendlich viele Lösungen von Werteverläufen. Deshalb wird eine spezielle Lösung für eine Anfangsbedingung ${\displaystyle y_{0}}$ und der unabhängigen Variablen ${\displaystyle x=0}$ bzw. bei zeitabhängigen Systemen ${\displaystyle t=0}$ gewählt. Die grafische Darstellung der Lösung einer DGL mit Berücksichtigung des Anfangswertes bezeichnet man als Trajektorie.

Die im Beispiel genannte Lösung der linearen DGL ${\displaystyle y(t)}$ stellt eine bekannte asymptotisch verlaufende e-Funktion im Zeitbereich dar.

Klassische Lösungsverfahren:

Die klassischen Lösungsverfahren von GDGL wie „Separation der Variablen“, „Exponentialansatz“, „Laplace-Transformation mit Partialbruchzerlegung“ oder „Laplace-Transformation mit Laplace-Transformationstabellen“ sind zum Teil aufwendig.

Numerische zeitdiskrete Lösungsverfahren:

Erheblich einfacher ist die Lösung von linearen und nichtlinearen DGL-en 1. O. und den meisten linearen und nichtlinearen DGL höherer Ordnung durch Anwendung numerischer zeitdiskreter Verfahren. Der Approximationsfehler gegenüber der analytischen Funktion fällt beim Einschrittverfahren linear mit reduzierter Schrittweite ${\displaystyle \Delta t}$. Partielle Differenzialgleichungen können oft nur mit numerischen Methoden approximiert werden.

Siehe auch in diesem Artikel Übersicht Numerik: ${\displaystyle \to }$ #Lösung von linearen gewöhnlichen Differenzialgleichungen mittels der numerischen Berechnung.

Anmerkung: Die Begriffe „Nichtlineare DGL“ und „Nichtlineares dynamisches System“ unterscheiden sich, wobei ein dynamisches System auch nichtlineare statische Funktionen wie „Begrenzungseffekte“, Hysterese, „Nichtlineare Kennlinie“ oder „Totzone“ enthalten kann, die nicht mit DGL-en beschrieben werden können. Diese Systeme mit statischen Nichtlinearitäten können durch numerische Methoden in Verbindung mit logischen Befehlen dem tatsächlichen Systemverhalten angenähert werden.

Siehe auch ${\displaystyle \to }$ Differentialgleichung

Siehe auch ${\displaystyle \to }$ Lineare gewöhnliche Differentialgleichung

Seien ${\displaystyle \Omega \subseteq \mathbb {R} \times \left(\mathbb {R} ^{m}\right)^{n+1},n\in \mathbb {N} }$ und ${\displaystyle f\colon \Omega \to \mathbb {R} ^{m}}$ eine stetige Funktion. Dann heißt

${\displaystyle f\left(x,y,y',y'',\dotsc ,y^{(n)}\right)=0}$

ein gewöhnliches Differentialgleichungssystem ${\displaystyle n}$-ter Ordnung von ${\displaystyle m}$ Gleichungen (${\displaystyle x}$ ist hier die unabhängige Variable, ${\displaystyle y'={\tfrac {dy}{dx}}}$ usw.). Im Fall ${\displaystyle m=1}$ nennt man dies eine gewöhnliche Differentialgleichung ${\displaystyle n}$-ter Ordnung.

Ihre Lösungen sind ${\displaystyle n}$-mal differenzierbare Funktionen ${\displaystyle y\colon I\to \mathbb {R} ^{m}}$, welche die Differentialgleichung auf einem zu bestimmenden Intervall ${\displaystyle I\subset \mathbb {R} }$ erfüllen. Sucht man eine spezielle Lösung, welche zu gegebenen ${\displaystyle x_{0}\in I}$ und ${\displaystyle y_{0},\dotsc ,y_{n-1}\in \mathbb {R} ^{m}}$ zusätzlich

${\displaystyle y(x_{0})=y_{0},\;y'(x_{0})=y_{1},\dotsc ,y^{(n-1)}(x_{0})=y_{n-1}}$

erfüllt, so bezeichnet man dies als Anfangswertproblem.

Kann die Differentialgleichung nach der höchsten vorkommenden Ableitung aufgelöst werden und hat somit die Form

${\displaystyle y^{(n)}=f\left(x,y,y',y'',\dotsc ,y^{(n-1)}\right)}$,

so heißt sie explizit, andernfalls implizit; siehe auch Satz von der impliziten Funktion.

In der Literatur zu gewöhnlichen Differentialgleichungen werden standardmäßig zwei unterschiedliche Notationen verwendet. In der einen Variante wird die unabhängige Variable mit ${\displaystyle x}$ bezeichnet und die Ableitungen der Funktion ${\displaystyle y}$ nach ${\displaystyle x}$ mit ${\displaystyle y',y''}$ usw. Die andere Schule verwendet eine auf Newton zurückgehende Notation. Dabei ist die unabhängige Variable ${\displaystyle t}$ bereits mit einem Sinn versehen; ${\displaystyle t}$ ist die Zeit. Lösungen werden dann oft mit ${\displaystyle x}$ bezeichnet und die Ableitungen nach der Zeit werden als ${\displaystyle {\dot {x}},{\ddot {x}}}$ notiert. Da dieser Artikel von Vertretern beider Schulen bearbeitet wurde, finden sich beide Notationen wieder.

Ob überhaupt eine Lösung existiert, lässt sich anhand einiger Kriterien erkennen. Die Differentialgleichung selbst reicht im Allgemeinen nicht aus, um die Lösung eindeutig zu bestimmen.

Beispielsweise ist der grundsätzliche Bewegungsablauf aller schwingenden Pendel gleich und kann durch eine einzige Differentialgleichung beschrieben werden. Der konkrete Bewegungsablauf ist jedoch durch die Rand- oder Anfangsbedingung(en) (wann wurde das Pendel angestoßen, und wie groß ist die Anfangsauslenkung) bestimmt.

Die lokale Lösbarkeit von Anfangswertproblemen bei gewöhnlichen Differentialgleichungen erster Ordnung wird durch den Satz von Picard-Lindelöf und den Satz von Peano beschrieben. Aus der Existenz einer lokalen Lösung kann man in einem zweiten Schritt auf die Existenz einer nicht-fortsetzbaren Lösung schließen. Mit Hilfe des Satzes vom maximalen Existenzintervall kann man darauf aufbauend von dieser nicht-fortsetzbaren Lösung dann gelegentlich Globalität nachweisen. Die Eindeutigkeit bekommt man als Anwendung der gronwallschen Ungleichung.

Gewöhnliche Differentialgleichungen beliebiger Ordnung lassen sich immer auf ein System von gewöhnlichen Differentialgleichungen erster Ordnung zurückführen. Hat eine gewöhnliche Differentialgleichung die Ordnung ${\displaystyle n}$, so führt man dazu die voneinander abhängigen Funktionen ${\displaystyle y_{1},y_{2},\dotsc ,y_{n}}$ ein:

${\displaystyle {\begin{aligned}y_{1}&:=y\\y_{2}&:=y'_{1}\\y_{3}&:=y'_{2}\\&\vdots \\y_{n}&:=y'_{n-1}\\\end{aligned}}}$

Aus der expliziten Differentialgleichung ${\displaystyle n}$-ter Ordnung für ${\displaystyle y}$ wird dabei:

${\displaystyle y'_{n}=f(x,y_{1},\ldots ,y_{n})}$

Man erhält also ein System von ${\displaystyle n}$ gewöhnlichen Differentialgleichungen erster Ordnung:

${\displaystyle (y_{1},\dotsc ,y_{n-1},y_{n})'=(y_{2},\dotsc ,y_{n},f(x,y_{1},\ldots ,y_{n}))}$.

Umgekehrt kann man aus manchen Differentialgleichungssystemen eine einzige Differentialgleichung höherer Ordnung erzeugen.

• Ein einfaches Beispiel aus der Physik ist das Zerfallsgesetz:

${\displaystyle {\dot {N}}\sim N}$

Dieses besagt, dass bei einer Menge instabiler Atome die Anzahl der zerfallenden Atome von der gesamten Anzahl ${\displaystyle N}$ der vorhandenen Atome proportional abhängt.

• Eine wichtige Klasse weiterer Differentialgleichungen bilden die newtonschen Bewegungsgleichungen:

${\displaystyle m\cdot {\ddot {\vec {r}}}(t)={\vec {F}}\left({\vec {r}}(t),t\right)}$

Durch die Kenntnis der von der Zeit ${\displaystyle t}$ und der Position ${\displaystyle r}$ eines Teilchens abhängenden Kraft ${\displaystyle F}$ treffen diese Gleichungen Aussagen über die Bewegung des Teilchens selbst.

• Neben einfachen Zusammenhängen der Änderungen einer einzelnen Größe lassen sich aber auch Vorhersagen über mehrere Größen in einem System treffen. In etwa die Lotka-Volterra-Gleichungen der Ökologie:

${\displaystyle {\dot {r}}=Z_{r}rb-M_{r}r}$

${\displaystyle {\dot {b}}=Z_{b}b-M_{b}rb}$

Dieses System beschreibt die zeitliche Veränderung der Räuberpopulation ${\displaystyle r}$ und der Beutepopulation ${\displaystyle b}$ bei konstanten natürlichen Geburtenraten ${\displaystyle Z}$ und Sterberaten ${\displaystyle M}$. Einige wichtige Eigenschaften dieses Modells lassen sich in Form der sogenannten Lotka-Volterra-Regeln zusammenfassen. Dieses und ähnliche Systeme finden in der theoretischen Biologie auch zur Beschreibung von Ausbreitungsprozessen und in Epidemiemodellen breite Anwendung.

Den bekanntesten Typ der gewöhnlichen Differentialgleichungen bildet die lineare Differentialgleichung ${\displaystyle n}$-ter Ordnung mit:

${\displaystyle \sum _{i=0}^{n}a_{i}(x)y^{(i)}(x)=b(x)}$ für stetige ${\displaystyle a_{i}\colon \mathbb {R} \rightarrow \mathbb {R} }$.

Weitere wichtige Typen von gewöhnlichen Differentialgleichungen sind die folgenden:

• d’Alembertsche Differentialgleichung

${\displaystyle y(x)=xg(y'(x))+f(y'(x))\,}$.

• Bernoullische Differentialgleichung

${\displaystyle y'(x)=f(x)y(x)+g(x)y^{\alpha }(x)\,}$ mit ${\displaystyle \alpha \neq 1}$.

• Exakte Differentialgleichung

${\displaystyle p\left(x,y(x)\right)+q(x,y(x))y'(x)=0\,}$, worin das Vektorfeld ${\displaystyle (p,q)}$ eine Potentialfunktion besitzt.

• Jacobische Differentialgleichung

${\displaystyle y'(x)=f\left({\frac {ax+by(x)+c}{\alpha x+\beta y(x)+\gamma }}\right)}$.

• Lineares Differentialgleichungssystem erster Ordnung von ${\displaystyle m}$ Gleichungen

${\displaystyle \ y'(x)=A(x)y(x)+b(x)}$ für stetige ${\displaystyle A\colon \mathbb {R} \rightarrow \mathbb {R} ^{m\times m}}$ und ${\displaystyle b\colon \mathbb {R} \rightarrow \mathbb {R} ^{m}\,}$.

• Riccatische Differentialgleichung

${\displaystyle y'(x)=f(x)y^{2}(x)+g(x)y(x)+h(x)\,}$.

• Separierbare Differentialgleichung

${\displaystyle y'(x)=f\left(y(x)\right)g(x)\,}$.

Ein Differentialgleichungssystem heißt autonom oder zeitinvariant, falls die beschreibende Gleichung nicht von der unabhängigen Variable ${\displaystyle x}$ abhängt, d. h., falls das System von der Form

${\displaystyle f\left(y,y',y'',\dotsc ,y^{(n)}\right)=0}$

ist.

Ein Differentialgleichungssystem

${\displaystyle y'=f(y)\ ,\ y(0)=y_{0}\in \mathbb {R} ^{m}}$

heißt vollständig, wenn zu jedem Anfangswert ${\displaystyle y_{0}}$ die globale Lösung auf ganz ${\displaystyle \mathbb {R} }$ definiert und eindeutig ist. Dies ist z. B. der Fall, wenn ${\displaystyle f\colon \mathbb {R} ^{m}\rightarrow \mathbb {R} ^{m}}$ linear beschränkt und Lipschitz-stetig ist. Es bezeichne ${\displaystyle \varphi (\cdot ,y_{0})}$ diese (eindeutig bestimmte globale) Lösung. Dann nennt man ${\displaystyle \varphi \colon \mathbb {R} \times \mathbb {R} ^{m}\to \mathbb {R} ^{m}}$ den Fluss der Differentialgleichung ${\displaystyle y'=f(y)}$, und ${\displaystyle (\mathbb {R} ,\mathbb {R} ^{m},\varphi )}$ bildet dann ein dynamisches System.

Besonders einfach zu analysieren ist der Fall ${\displaystyle n=1,\ m=2}$ der ebenen autonomen Systeme. Mit Hilfe des Satzes von Poincaré und Bendixson kann man oft die Existenz periodischer Lösungen nachweisen. Ein wichtiges ebenes autonomes System bildet das Lotka-Volterra-Modell.

Da die Poincaré-Bendixson-Theorie zentral auf den jordanschen Kurvensatz aufbaut, sind höherdimensionale Analoga falsch. Insbesondere ist es sehr schwierig, periodische Lösungen höherdimensionaler autonomer Systeme zu finden.

Durch gewöhnliche Differentialgleichungen lassen sich viele dynamische Systeme aus der Technik, Natur und Gesellschaft beschreiben. Viele auf den ersten Blick sehr verschiedene physikalische Probleme lassen sich mit der GDGL jedoch formal identisch darstellen.

Ein dynamisches System ist eine Funktionseinheit zur Verarbeitung und Übertragung von Signalen, wobei die Eingangsgröße ${\displaystyle u(t)}$ als Ursache und die Ausgangsgröße ${\displaystyle y(t)}$ als Folge des zeitlichen Übertragungsverhaltens des Systems definiert ist. Ist die Eingangsgröße ${\displaystyle u(t)=0}$, so handelt es sich um eine homogene GDGL, anderenfalls um eine inhomogene GDGL.

Ein dynamisches System verhält sich linear, wenn die Wirkungen zweier linear überlagerter Eingangssignale sich am Ausgang des Systems in gleicher Weise linear überlagern. Eine lineare GDGL enthält die gesuchte Funktion und deren Ableitungen nur in der ersten Potenz. Es dürfen keine Produkte der gesuchten Funktion und ihren Ableitungen auftreten. Die gesuchte Funktion darf auch nicht in Argumenten von Winkelfunktionen, Logarithmen usw. erscheinen.

Ein bekanntes Beispiel aus der Mechanik ist die lineare GDGL zweiter Ordnung eines gedämpften Federpendels mit der Federsteifigkeit ${\displaystyle c}$, Masse ${\displaystyle m}$ und Dämpfungskonstante ${\displaystyle d}$. Dabei ist die Eingangsgröße: die Kraft ${\displaystyle F}$, die Ausgangsgröße der Weg ${\displaystyle x}$.

${\displaystyle {\ddot {x}}(t)+{\frac {d}{m}}\cdot {\dot {x}}(t)+{\frac {c}{m}}\cdot x(t)={\frac {1}{m}}\cdot F(t)}$.

Linear zeitinvariante Systeme können durch die nachfolgenden Verfahren berechnet werden:

• Klassisch mit Hilfe des Exponentialansatzes,
• Laplace-Transformation,
• Numerisch.

Die Lösung einer inhomogenen GDGL besteht aus der allgemeinen Lösung der homogenen GDGL plus einer speziellen Lösung (partikuläre Lösung) der inhomogenen GDGL. Deshalb erfolgt das Lösungsverfahren der inhomogenen GDGL, unabhängig von der Ordnung, in zwei Stufen. Die Gesamtlösung ist die Summe der beiden Lösungen:

• Die Lösung der homogenen GDGL beschreibt das Systemverhalten mit Anfangswerten der Systemspeicher zum Zeitpunkt ${\displaystyle t=0}$ und dem Eingangssignal ${\displaystyle u(t)=0}$. Dies bedeutet für das dynamische System, es ist sich selbst überlassen und hat nur ein Ausgangssignal. Die Lösung der inhomogenen GDGL ist Null, wenn alle Anfangsbedingungen von ${\displaystyle y_{0}=0}$ und deren Ableitungen Null sind.

• Die partikuläre Lösung der GDGL beschreibt das Übertragungsverhalten von ${\displaystyle y(t)}$ für ${\displaystyle u(t)\neq 0}$ als erzwungene Bewegung. Je nach Systemordnung müssen alle Anfangsbedingungen ${\displaystyle y_{0}=0}$ und deren Ableitungen Null sein.

Ist die Übertragungsfunktion ${\displaystyle G(s)}$ als Laplace-transformierte GDGL gegeben, so ist die Berechnung des System-Ausgangssignals ${\displaystyle Y(s)}$ für ein gegebenes Eingangssignal ${\displaystyle U(s)}$ bei Anwendung der inversen Laplace-Transformation immer eine partikuläre Lösung. Die partikuläre Lösung der GDGL ist in der Regelungstechnik meist von hauptsächlichem Interesse.

Mit Hilfe des Exponentialansatzes und der sich daraus ergebenden charakteristischen Gleichung lassen sich auch GDGL höherer Ordnung lösen. Dieser Exponentialansatz gilt als universelles Lösungsverfahren für homogene GDGL beliebiger Ordnungen mit konstanten Koeffizienten.

Hat eine GDGL die Ordnung n, so hat ihre Lösung n Integrationskonstanten. Dazu müssen n Anfangsbedingungen gegeben sein.

Der Exponentialansatz ${\displaystyle y(t)=e^{\lambda \cdot t}}$ liefert Ableitungen der Form: ${\displaystyle y^{(n)}(t)=\lambda ^{n}\cdot e^{\lambda \cdot t}}$.

Werden diese Beziehungen in die homogene GDGL eingesetzt, entsteht die charakteristische Gleichung als Polynom n-ter Ordnung für ${\displaystyle \lambda }$. Die Lösung der homogenen zu einer inhomogenen Differenzialgleichung gehörenden Differenzialgleichung lautet damit allgemein für den Fall reeller ungleicher Nullstellen ${\displaystyle \lambda _{i}}$ des charakteristischen Polynoms:

${\displaystyle y_{H}(t)=C_{1}\cdot e^{{\lambda }_{1}\cdot t}+C_{2}\cdot e^{{\lambda }_{2}\cdot t}+\cdots +C_{n}\cdot e^{{\lambda }_{n}\cdot t}}$

Die Lösung einer GDGL erfolgt durch Integration. Jede Integration ergibt Integrationskonstanten ${\displaystyle C_{i}}$, deren Anzahl durch die Ordnung der GDGL bestimmt ist. Die Lösung einer GDGL n-ter Ordnung enthält ${\displaystyle n}$ voneinander unabhängige Integrationskonstanten. Diese sind für eine spezielle (partikuläre) Lösung der GDGL abhängig von den Eigenwerten und gegebenen Anfangsbedingungen des Übertragungssystems zu bestimmen.

Die Bestimmung der Integrationskonstanten ${\displaystyle C_{i}}$ bei Systemen höherer Ordnung (> 2) ist sehr umständlich. Weitere Informationen liefert die Fachliteratur.^[2]

Eine homogene GDGL n-ter Ordnung hat ${\displaystyle n}$ Anfangswerte. Für die homogene GDGL zweiter Ordnung mit zwei vorzugebenden Anfangswerten ${\displaystyle y_{0}}$ und ${\displaystyle {\dot {y}}_{0}}$ können die Koeffizienten ${\displaystyle C_{1}}$ und ${\displaystyle C_{2}}$ errechnet werden, wenn die Nullstellen des charakteristischen Polynoms bekannt sind.

Für jede Anfangsbedingung ergibt sich eine Gleichung (${\displaystyle y_{H}(0)=y_{0}}$, ${\displaystyle {\dot {y}}_{H}(0)={\dot {y}}_{0}}$).

Beispiel für eine homogene GDGL mit zwei reellen Nullstellen ${\displaystyle \lambda _{1}=-0{,}5}$ und ${\displaystyle \lambda _{2}=-1}$ und Anfangswerten ${\displaystyle {\dot {y}}_{0}=1}$; ${\displaystyle y_{0}=1}$:

Lösung ${\displaystyle y_{H}(t)}$ der homogenen DGL 2. Ordnung:

${\displaystyle y_{H}(t)=C_{1}\cdot e^{-0{,}5\cdot t}+C_{2}\cdot e^{-1\cdot t}}$

Berechnung der Koeffizienten:

${\displaystyle y_{0}\ {\xrightarrow {t=0}}1=C_{1}+C_{2}}$

${\displaystyle {\dot {y}}_{0}{\xrightarrow {d/dt}}1=C_{1}\cdot -0{,}5\cdot e^{-0{,}5\cdot t}+C_{2}\cdot -1\cdot e^{-1\cdot t}}$

${\displaystyle {\dot {y}}_{0}{\xrightarrow {t=0}}1=C_{1}\cdot -0{,}5+C_{2}\cdot -1=-0{,}5\cdot C_{1}-C_{2}}$

Aus den beiden Gleichungen von ${\displaystyle y_{0}}$ für ${\displaystyle t=0}$ und ${\displaystyle {\dot {y}}_{0}}$ für ${\displaystyle t=0}$ lassen sich die Koeffizienten ${\displaystyle C_{1}}$ und ${\displaystyle C_{2}}$ bestimmen.

Anmerkung: Die Ableitung nach ${\displaystyle t}$ von ${\displaystyle e^{-a\cdot t}}$ ist ${\displaystyle -a\cdot e^{-a\cdot t}}$.

Tabelle: Durch die verschiedenen Arten der Lösungen der quadratischen Gleichung, bedingt durch die Größe der Diskriminante, ergeben sich drei unterschiedliche Fälle der Eigenwerte λ der GDGL wie:

Lösung der homogenen linearen Differenzialgleichung 2. Ordnung mit konstanten Koeffizienten	Nullstellen	Anfangswertproblem Bestimmung C1, C2
Radikand > 0: 2 reelle Nullstellen ${\displaystyle y_{H}(t)=C_{1}\cdot e^{{\lambda }_{1}\cdot t}+C_{2}\cdot e^{{\lambda }_{2}\cdot t}}$	${\displaystyle {\lambda }_{1;2}=-{\frac {a_{1}}{2}}\pm {\sqrt {{\frac {{a_{1}}^{2}}{4}}-a_{0}}}}$	${\displaystyle C_{1}={\frac {{\dot {y}}_{0}-y_{0}\cdot \lambda _{2}}{\lambda _{1}-\lambda _{2}}}\,}$ ${\displaystyle C_{2}=y_{0}-C_{1}\,}$
Radikand = 0: 2 gleiche Nullstellen ${\displaystyle y_{H}(t)=C_{1}\cdot e^{{\lambda }_{1}\cdot t}+C_{2}\cdot t\cdot e^{{\lambda }_{1}\cdot t}}$	${\displaystyle \lambda =\lambda _{1;2}=-{\frac {a_{1}}{2}}}$	${\displaystyle C_{1}=y_{0}\,}$ ${\displaystyle C_{2}={\dot {y}}_{0}-y_{0}\cdot \lambda \,}$
Radikand < 0: konjugiert komplexen Nullstellen ${\displaystyle y_{H}(t)=e^{\alpha \cdot t}\cdot [C_{1}\cdot \cos(\beta \cdot t)+C_{2}\cdot \sin(\beta \cdot t)]}$	${\displaystyle {\lambda }_{1;2}=\alpha \pm i\cdot \beta }$ ${\displaystyle \alpha =-a_{1}/2\,}$ ${\displaystyle \beta ={\sqrt {a_{0}-{\frac {{a_{1}}^{2}}{4}}}}}$	${\displaystyle C_{1}={\frac {{\dot {y}}_{0}-\alpha \cdot y_{0}}{\beta }}}$ ${\displaystyle C_{2}=y_{0}\,}$

(c) HeinrichKü in der Wikipedia auf Deutsch, CC BY-SA 3.0

Übertragungsfunktion eines dynamischen Systems bestehend aus zwei PT1-Gliedern ${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{(2\cdot s+1)\cdot (s+1)}}={\frac {1}{2\cdot s^{2}+3\cdot s+1}}}$ Zugehörige systembeschreibende GDGL: ${\displaystyle 2\cdot {\ddot {y}}(t)+3\cdot {\dot {y}}(t)+y(t)=u(t)}$ Die höchste Ableitung freigestellt: ${\displaystyle {\ddot {y}}(t)+1{,}5\cdot {\dot {y}}(t)+0{,}5\cdot y(t)=0{,}5\cdot u(t)\qquad {\text{Koeffizienten:}}\ a_{1}=1{,}5\quad a_{0}=0{,}5\quad b_{0}=0{,}5}$ Vorgegeben: Willkürlich gewählte Anfangswerte der Energiespeicher (Integratoren): ${\displaystyle y'_{0}(t)=1}$; ${\displaystyle y_{0}(t)=1}$; Vorgegeben: Eingangsgröße ${\displaystyle u(t)=1}$ ist eine normierte Sprungfunktion für ${\displaystyle t>0}$. Gesucht: Lösung der zugehörigen homogenen GDGL ${\displaystyle y_{H}(t)}$ und partikuläre Lösung ${\displaystyle y_{p}(t)}$: Für die Lösung der homogenen GDGL wird ${\displaystyle u(t)=0}$ gesetzt. Errechnet laut der oben dargestellten Tabelle der Lösung der homogenen GDGL Es ergeben sich zwei reelle Nullstellen: ${\displaystyle {\lambda }_{1}=-0{,}5;\quad {\lambda }_{2}=-1}$ Errechnet: Die Integrationskonstanten errechnen sich laut Tabelle mit ${\displaystyle C_{1}=4}$; ${\displaystyle C_{2}=-3}$. Analytische Lösung der homogenen GDGL laut Tabelle für zwei reelle Nullstellen: ${\displaystyle y_{H}(t)=C_{1}\cdot e^{{\lambda }_{1}\cdot t}+C_{2}\cdot e^{{\lambda }_{2}\cdot t}\qquad \to }$ daraus folgt: Mit den eingesetzten Zahlenwerten lautet die analytische Lösung der homogenen GDGL: ${\displaystyle {\underline {\underline {y_{H}(t)=4\cdot e^{-0{,}5\cdot t}-3\cdot e^{-t}}}}}$ Partikuläre Lösung: Die Berechnung der Systemantwort ${\displaystyle y_{p}(t)}$ des Eingangs-Ausgangsverhaltens über das Faltungsintegral ist aufwendig. Einfacher ist die Lösung – wie nachfolgend dargestellt – durch die Anwendung der Laplace-Transformation.

Die allgemeine Form einer Differentialgleichung mit konstanten Koeffizienten ${\displaystyle a_{i}}$ der Ausgangsgröße ${\displaystyle y(t)}$ und mit ${\displaystyle b_{i}}$ der Eingangsgröße ${\displaystyle u(t)}$ lautet:

${\displaystyle a_{n}\cdot y^{(n)}(t)+\ \cdots \ +a_{2}\cdot {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)+b_{1}\cdot {\dot {u}}(t)+b_{2}\cdot {\ddot {u}}(t)+\ \cdots \ +b_{m}\cdot u^{(m)}(t)}$.

Durch Anwendung des Laplace-Differentiationssatzes einer GDGL entstehen algebraische Gleichungen mit sogenannten Zähler- und Nennerpolynomen. ${\displaystyle s=\delta +j\cdot \omega }$ ist die komplexe Laplace-Variable, die mit einem Exponenten anstelle der Ordnung einer Ableitung steht. Die Übertragungsfunktion ${\displaystyle G(s)}$ ist definiert als das Verhältnis des Ausgangssignals ${\displaystyle Y(s)}$ zum Eingangssignal ${\displaystyle U(s)}$, wobei die Anfangswerte des Systems gleich Null sind.

${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\dotsb +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\dotsb +a_{2}s^{2}+a_{1}s+a_{0}}}}$.

Die Berechnung des Zeitverhaltens eines Übertragungssystems aus der Übertragungsfunktion ${\displaystyle G(s)}$ wird üblicherweise für normierte Eingangssignale ${\displaystyle U(s)}$ durchgeführt. Zur Berechnung der Sprungantwort mit dem Eingangssignal ${\displaystyle u(t)=1(t):=U(s):={\frac {1}{s}}}$ wird der Übertragungsfunktion der Term ${\displaystyle {\frac {1}{s}}}$ multiplikativ angehängt. Wird letzteres nicht durchgeführt, erhält man an Stelle der Sprungantwort die Impulsantwort.

Übertragungsfunktion in Polynomdarstellung, Pol-Nullstellendarstellung und Zeitkonstantendarstellung:

Die Pole und Nullstellen der Übertragungsfunktion sind die wichtigsten Kenngrößen des Systemverhaltens. Die Pole (Nullstellen des Nennerpolynoms) sind gleichzeitig die Lösung des Systems und bestimmen das System-Zeitverhalten. Die Nullstellen des Zählerpolynoms haben nur Einfluss auf die Amplituden der Systemantwort.

${\displaystyle {\begin{aligned}G(s)&={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\dotsb +b_{1}s+b_{0}}{a_{n}s^{n}+a_{n-1}s^{n-1}+\dotsb +a_{1}s+a_{0}}}\\\\&=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{(s-s_{p1})(s-s_{p2})\dotsm (s-s_{pn})}}=K\cdot {\frac {(T_{v1}\cdot s+1)(T_{v2}\cdot s+1)\cdots }{(T_{1}\cdot s+1)(T_{2}\cdot s+1)\cdots }}\end{aligned}}}$

Die Lösung erfolgt durch Partialbruch-Zerlegung der Produktdarstellung in einfache additive Terme, die sich leicht in den Zeitbereich transformieren lassen. Die Partialbruch-Zerlegung von Übertragungsfunktionen höherer Ordnung ist nicht immer einfach, insbesondere wenn konjugiert komplexe Nullstellen vorliegen.

Alternativ können Laplace-Transformationstabellen benutzt werden, welche die häufigsten korrespondierenden Gleichungen im Zeitbereich enthalten.

Die partikuläre Lösung beschreibt das Übertragungsverhalten des Systems als Funktion des Eingangssignals ${\displaystyle u(t)}$ und ist meist von hauptsächlichem Interesse. Die Anfangsbedingungen ${\displaystyle y_{0}}$ und ${\displaystyle {\dot {y}}_{0}}$ haben dabei den Wert 0.^[3]

Lösung der gegebenen GDGL 2. Ordnung:

${\displaystyle {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)}$.

Die Übertragungsfunktion eines Systems entsteht nach dem Differentiationssatz durch Austausch der zeitabhängigen Terme einer GDGL mit den Laplace-Transformierten. Voraussetzung ist, dass die Anfangsbedingung des Systems Null ist. Je nach Grad der Ableitungen einer Funktion y(t) entstehen nach der Transformation folgende Laplace-Transformierte Y(s):

${\displaystyle s^{2}\cdot Y(s)+a_{1}\cdot s\cdot Y(s)+a_{0}\cdot Y(s)=b_{0}\cdot U(s)}$

Mit den transformierten Termen kann die Übertragungsfunktion des dynamischen Systems G(s) aufgestellt werden:

${\displaystyle G(s)={\frac {Y}{U}}(s)={\frac {b_{0}}{s^{2}+a_{1}\cdot s+a_{0}}}}$

Polynome einer Übertragungsfunktion werden durch Nullstellenbestimmungen in Linearfaktoren (Grundpolynome: Monom, Binom und Trinom) zerlegt. Liegen Zahlenwerte der Koeffizienten einer Übertragungsfunktion 2. Ordnung vor, können die Pole (= Nullstellen im Nenner der Übertragungsfunktion) durch die bekannte Formel zur Lösung einer gemischt-quadratischen Gleichung ermittelt werden.

Durch die verschiedenen Arten der Lösungen der Pole bedingt durch die Größe des Radikanden der quadratischen Gleichung ergeben sich drei unterschiedliche Fälle der Eigenwerte ${\displaystyle s_{i}}$ (der Pole ${\displaystyle s_{pi}}$) der Übertragungsfunktion. Nachfolgend ist eine Korrespondenztabelle des s-Bereichs mit ${\displaystyle Y(s)=U(s)\cdot G(s)}$ und des Zeitbereichs für ${\displaystyle y(t)}$ für einen transformierten Eingangssprung ${\displaystyle u(t)=1(t)\to \ U(s):=1/s}$.

Folgende Grundpolynome (Binome und Trinome bei konjugiert komplexen Polen) entstehen in Abhängigkeit von den Nullstellen. Die Lösungen der Übertragungsfunktionen als Sprungantwort im Zeitbereich sind einer Laplace-Transformationstabelle entnommen worden:

Die Laplace-Transformationstabellen können in zwei Formen der Produkt-Darstellung aufgeführt sein, wobei unterschiedliche Faktoren a₀ und K berücksichtigt werden müssen. Die Umrechnung der Pole-Nullstellen-Darstellung in Zeitkonstanten-Darstellung ist einfach, sie sind algebraisch identisch. ${\displaystyle T_{i}=1/{s_{pi}}}$.

Pol-Nullstellen-Darstellung (Stabiles System) und Zeitkonstanten-Darstellung:

${\displaystyle G(s)={\frac {a_{0}}{(s+s_{p1})\cdot (s+s_{p2})}}={\frac {K}{(T_{1}\cdot s+1)\cdot (T_{2}\cdot s+1)}}}$

Tabelle: Berechnung der Sprungantworten ${\displaystyle y(t)}$ eines Übertragungssystems 2. Ordnung in Abhängigkeit von den Polstellenarten:

f(s) Übertragungsfunktion 2. Ordnung Eingangssprung u(t) = 1 := Multiplikation mit 1/s	f(t) Partikuläre Lösung Sprungantwort im Zeitbereich	Bestimmung der Pole ${\displaystyle s_{p1}}$ und ${\displaystyle s_{p2}}$ aus der Polynom-Darstellung
2 reelle Polstellen: ${\displaystyle Y(s)={\frac {1}{s\cdot (T_{1}\cdot s+1)\cdot (T_{2}\cdot s+1)}}}$	${\displaystyle y(t)=1-{\frac {1}{T_{1}-T_{2}}}\cdot }$ ${\displaystyle \cdot \left(T_{1}\cdot e^{-{\frac {t}{T_{1}}}}-{T_{2}\cdot e^{-{\frac {t}{T_{2}}}}}\right)}$	${\displaystyle s_{p1;2}=-{\frac {a_{1}}{2}}\pm {\sqrt {{\frac {{a_{1}}^{2}}{4}}-a_{0}}}}$ ${\displaystyle T_{1}=-{\frac {1}{s_{p1}}}\quad T_{2}=-{\frac {1}{s_{p2}}}}$
2 gleiche Polstellen: ${\displaystyle Y(s)={\frac {1}{s\cdot (T\cdot s+1)^{2}}}}$	${\displaystyle y(t)=1-{\frac {T+t}{T}}\cdot e^{-{\frac {t}{T}}}}$	${\displaystyle s_{p1}=s_{p2}=-{\frac {a_{1}}{2}}}$ ${\displaystyle T=-{\frac {1}{s_{p}}}}$
Konjugiert komplexe Polstellen: ${\displaystyle Y(s)={\frac {{\omega _{0}}^{2}}{s\cdot (s^{2}+2\cdot D\cdot \omega _{0}\cdot s+{\omega _{0}}^{2})}}\quad {\text{oder:}}}$ ${\displaystyle Y(s)={\frac {1}{s\cdot (T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1)}}}$ ${\displaystyle \omega _{0}={\text{ungedämpfte Kreisfrequenz}},\quad T=1/\omega _{0}}$	${\displaystyle y(t)=1-{\frac {1}{\sqrt {1-D^{2}}}}\cdot }$ ${\displaystyle \cdot e^{-D\cdot \omega _{0}\cdot t}\cdot \sin(\omega _{d}\cdot t+\phi )}$ ${\displaystyle \omega _{d}=\omega _{0}\cdot {\sqrt {1-D^{2}}}}$ ${\displaystyle \phi =\arccos(D)}$	${\displaystyle s_{p1;2}=-D\cdot \omega _{0}\pm j\omega _{0}\cdot {\sqrt {1-D^{2}}}}$ Dämpfung D:${\displaystyle \quad -1<D<1}$ ${\displaystyle D={\frac {a_{1}}{2\cdot {\sqrt {a_{0}}}}}}$

Wird für den Fall der zwei reellen Nullstellen in die Gleichung für ${\displaystyle f(t)\to T_{1}=T_{2}}$ eingesetzt, entsteht eine Division durch Null ${\displaystyle 1/(T_{1}-T_{1})}$, was nicht zulässig ist. Als „verschiedene“ Nullstellen gelten bereits Nullstellen, wenn sie sich in einer theoretisch unendlichen Dezimalstelle eines Wertes unterscheiden.

Die Gesamtlösung einer GDGL ergibt sich aus der Überlagerung der Systemantworten auf die Anfangsbedingungen und auf das Eingangssignal:

${\displaystyle y(t)=y_{H}(t)+y_{P}(t)}$

Die partikuläre Lösung der GDGL bezieht sich darauf, dass die Anfangswerte ${\displaystyle y_{0};\ {\dot {y}}_{0};\ {\ddot {y}}_{0}\dots }$ gleich Null sind und das Eingangssignal ${\displaystyle u(t)\neq 0}$ ist. Sie lässt sich aus der Übertragungsfunktion ${\displaystyle G(s)}$ bestimmen, indem die Differentialgleichung einer Laplace-Transformation unterzogen wird.

Vorgegeben: Eingangssignal: Sprungfunktion ${\displaystyle U(s)=1/s}$. Übertragungsfunktion des Systems: ${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{(2\cdot s+1)\cdot (s+1)}}\qquad T_{1}=2;\,T_{2}=1}$ Gesucht: Partikuläre Lösung ${\displaystyle y_{P}(t)}$ für die gegebene Übertragungsfunktion: Suchbegriff für die Laplace-Transformationstabelle: ${\displaystyle {Y(s)}={\frac {U(s)}{(2\cdot s+1)\cdot (s+1)}}={\frac {1}{s\cdot (2\cdot s+1)\cdot (s+1)}}\qquad T_{1}=2;\,T_{2}=1}$ Errechnet: Die gefundene analytische Gleichung ${\displaystyle f(t)}$ der partikulären Lösung laut Transformationstabelle durch Eingabe der Koeffizienten lautet: ${\displaystyle y_{p}(t)=1-{\frac {1}{T_{1}-T_{2}}}\cdot [T_{1}\cdot e^{-{\frac {t}{T_{1}}}}-T_{2}\cdot e^{-{\frac {t}{T_{2}}}}]}$. Zahlenwerte der Zeitkonstanten eingesetzt: ${\displaystyle {\underline {\underline {y_{p}(t)=\ 1-[2\cdot {e^{-{\frac {t}{2}}}-e^{-t}}]}}}}$. 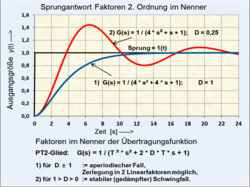Grafische Darstellung der partikulären Lösung siehe vorletztes Bild.

Anmerkung: Enthält die Ausgangsgröße eines Übertragungssystems Schwingungsanteile, ergeben sich laut Transformationstabellen aufwendige trigonometrische Gleichungen.

Eine lineare gewöhnliche Differentialgleichung (GDGL) mit konstanten Koeffizienten, die ein dynamisches System mit einem Eingangssignal und einem Ausgangssignal beschreibt, wird nach dem Differenzenverfahren in eine Differenzengleichung umgeformt, indem die Differentialquotienten der GDGL durch Differenzenquotienten ausgetauscht werden.

Eine Differenzengleichung ist eine numerisch lösbare rekursive Berechnungsvorschrift für eine diskret definierte Folge von nummerierten Folgeelementen bzw. Stützstellen ${\displaystyle y_{k}}$ im Abstand eines meist konstanten Intervalls ${\displaystyle \Delta x}$ oder bei zeitabhängigen Systemen ${\displaystyle \Delta t}$.

Mit dem Austausch des Differenzialquotienten durch einen Differenzenquotienten entsteht automatisch das rekursive Verhalten der Differenzengleichung, bei der sich je nach Ordnung ${\displaystyle n}$ jedes aktuelle Folgeelement ${\displaystyle y_{k}}$ sich auf ein oder mehrere zurückliegende Folgeelemente bezieht.

Die numerische Gesamtlösung des Systems erfolgt – bei einfachen Differenzengleichungen – rekursiv (sich selbst aufrufend) über viele Berechnungsfolgen ${\displaystyle k=(0,1,2,3,\dots ,k_{\mathrm {max} })}$ in meist je kleinen konstanten Zeitstufen. Die Form der Gesamtlösung ist damit tabellarisch für die gesuchten Werte ${\displaystyle y_{(k)}}$ (Stützpunkt, Knoten) eines Funktionsverlaufs im zeitlichen Abstand ${\displaystyle \Delta t}$.

Das einfachste und älteste Einschrittverfahren ist das explizite Euler-Verfahren. Zu den Einschrittverfahren gehören das Implizites Euler-Verfahren, das Differenzenverfahren, Runge-Kutta-Verfahren, Heun-Verfahren. Bei den Mehrschrittverfahren wird die Information aus den zuvor bereits errechneten Stützpunkten gebildet.

Bereits die Anwendung des Differenzenverfahrens für GDGL 2. Ordnung erfordert einen beträchtlichen algebraischen Aufwand. Anfangswerte ${\displaystyle y_{0}>0}$ können nicht verarbeitet werden.

Mit Hilfe des Signalflussplanes der Regelungsnormalform lassen sich GDGL dynamischer Systeme höherer Ordnung einfach lösen. Die systembeschreibende GDGL wird in expliziter Darstellung (geordnet nach der höchsten Ableitung y(t)) in ein Signalflussdiagramm gebracht, wobei die Anzahl der Ableitungen von y(t) die Anzahl der Integratoren bestimmen.^[4]

Beispiel einer GDGL 2. Ordnung eines dynamischen Systems:

${\displaystyle a\cdot y''(t)+b\cdot y'(t)+c\cdot y(t)=u(t);\qquad \qquad {\text{u(t) = normierter Sprung 1(t)}}}$

• Enthält die Gleichung 2 reelle negative Pole, handelt es sich um 2 Verzögerungsglieder (PT1-Glieder).
• Enthält die Gleichung ein konjugiert komplexes Polpaar, handelt es sich um ein Schwingungsglied (${\displaystyle PT2_{kk}}$-Glied).

Für die Anwendung der Regelungsnormalform wird die höchste Ableitung der GDGL freigestellt und die Gleichung durch den Koeffizienten a dividiert.:

${\displaystyle y''(t)={\frac {b}{a}}\cdot y'(t)+{\frac {c}{a}}\cdot y(t)={\frac {1}{a}}\cdot {u}(t)}$

Dieser Signalflussplan der Regelungsnormalform für eine beliebige Ordnung lässt sich numerisch leicht berechnen. Für jede Ableitung der GDGL muss numerisch eine Differenzengleichung der Integration (I-Glied) mit den zugehörigen Koeffizienten berechnet werden. Jede Integration einer Ableitung wird mit den zugehörigen Koeffizienten als Zustandsvariable negativ auf den Wert der höchsten Ableitung zurückgeführt.

Sind Anfangswerte gegeben, werden die Integratoren direkt auf die Anfangswerte gesetzt, d. h. die tabellarisch geordneten Folgeglieder der numerisch berechneten Integratoren starteten mit den Anfangswerten. Normalerweise ist dabei ${\displaystyle u(t)=0}$.

→ Siehe ausführliche Details mit Anwendung Differenzengleichung (Differenzenverfahren)

→ Siehe auch Artikel Seminumerischer Algorithmus

Einige CAS können Differentialgleichungen lösen, z. B.:

• Maple:^[5] dsolve
• SageMath:^[6] desolve
• Xcas:^[7] desolve(y'=k*y,y)

• Partielle Differentialgleichung
• Anfangswertproblem
• Randwertproblem

• Jürgen Koch / Martin Stämpfle: Mathematik für das Ingenieurstudium 4. Auflage 2018, Carl Hanser Verlag München, ISBN 978-3-446-45166-7
• Herbert Amann: Gewöhnliche Differentialgleichungen, 2. Auflage, Gruyter – de Gruyter Lehrbücher, Berlin New York, 1995, ISBN 3-11-014582-0
• Bernd Aulbach: Gewöhnliche Differenzialgleichungen, Elsevier Spektrum Akademischer Verlag, Heidelberg, 2004, ISBN 3-8274-1492-X
• Harro Heuser: Gewöhnliche Differentialgleichungen, Teubner, März 2004, ISBN 3-519-32227-7
• Edward Lincey Ince: Die Integration gewöhnlicher Differentialgleichungen, Dover Publications, 1956, ISBN 0-486-60349-0
• Wolfgang Walter: Gewöhnliche Differentialgleichungen, Springer, 2000, ISBN 3-540-67642-2

1. ↑ Fachbuch: Jürgen Koch / Martin Stämpfle: „Mathematik für das Ingenieurstudium“, Kapitel: „Gewöhnliche Differenzialgleichungen“, „Lineare Differenzialgleichungen“.
2. ↑ May-Britt Kallenrode, Universität Osnabrück, Fachbereich Physik: Vorlesungsskript „Mathematik für Physiker“, Kapitel: „Gewöhnliche Differenzialgleichungen“, 611 Seiten, ausgestellt 2007.
3. ↑ Oliver Nelles, Universität Siegen: Vorlesungskonzept Mess- und Regelungstechnik I, Kapitel: „Laplace-Transformation“, 446 Seiten vom 8. Oktober 2009.
4. ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6. Siehe Kapitel: "Normalformen von Übertragungssystemen"
5. ↑ dsolve - Maple Programming Help. Abgerufen am 17. Mai 2020. 
6. ↑ Basic Algebra and Calculus — Sage Tutorial v9.0. Abgerufen am 17. Mai 2020. 
7. ↑ Symbolic algebra and Mathematics with Xcas. Abgerufen am 17. Mai 2020.