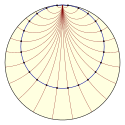
Geodätischer Fluss

In Mathematik und Physik beschreibt der geodätische Fluss eine Bewegung entlang kürzester Verbindungsstrecken (Geodäten). Weil Geodäten nicht nur von ihrem Ausgangspunkt, sondern auch von ihrer Ausgangsrichtung abhängen, kann der geodätische Fluss nur auf dem Tangentialbündel definiert werden.

Definition

Es sei ${\displaystyle M}$ eine vollständige Riemannsche Mannigfaltigkeit mit Tangentialbündel ${\displaystyle TM}$. Nach dem Satz von Hopf-Rinow gibt es für jeden Tangentialvektor ${\displaystyle v\in T_{x}M,x\in M}$ eine eindeutige Geodäte

${\displaystyle \gamma _{v}\colon (-\infty ,\infty )\to M}$

mit

${\displaystyle \gamma _{v}(0)=x,{\dot {\gamma }}_{v}(0)=v}$.

Wir definieren nun

${\displaystyle \phi \colon TM\times (-\infty ,\infty )\to TM}$

durch

${\displaystyle \phi (v,t):={\dot {\gamma }}_{v}(t)}$.

Dies definiert einen Fluss auf ${\displaystyle TM}$, d. h. es gilt ${\displaystyle \phi (v,s+t)=\phi (\phi (v,t),s)}$ und ${\displaystyle \phi (v,0)=v}$.

Häufig wird auch die Einschränkung des geodätischen Flusses auf das Einheitstangentialbündel ${\displaystyle T^{1}M}$ als geodätischer Fluss bezeichnet.

Geodätischer Fluss als Hamiltonscher Fluss

Der geodätische Fluss ist der Hamiltonsche Fluss der in lokalen Koordinaten durch

${\displaystyle H(x,p):={\frac {1}{2}}\sum _{i,j}g^{ij}(x)p_{i}p_{j}}$ gegebenen Hamilton-Funktion

${\displaystyle H\colon T^{*}M\to \mathbb {R} }$.

Hierbei bezeichnet ${\displaystyle g^{ij}(x)}$ die Einträge der zur Riemannschen Metrik ${\displaystyle g_{ij}(x)}$ inversen Matrix.

Physik

Die Eulerschen Gleichungen für die Bewegung eines starren Körpers lassen sich interpretieren als geodätischer Fluss auf der Lie-Gruppe ${\displaystyle \mathrm {Isom} (\mathbb {R} ^{3})}$.

Die Eulerschen Gleichungen zur Fluiddynamik eines inviskosen inkompressiblen Flusses lassen sich interpretieren als geodätischer Fluss auf der unendlich-dimensionalen Lie-Gruppe ${\displaystyle \mathrm {Sdiff} (\mathbb {R} ^{3})}$ der maßerhaltenden Abbildungen.

Beide Interpretationen gehen auf Wladimir Arnold zurück.^[1]

Geodätischer Fluss auf Mannigfaltigkeiten nichtpositiver Schnittkrümmung

Im Folgenden sei ${\displaystyle M}$ eine Riemannsche Mannigfaltigkeit nichtpositiver Schnittkrümmung.

Maßtheorie

Der geodätische Fluss erhält das Liouville-Maß. Wenn ${\displaystyle M}$ kompakt ist, dann ist der geodätische Fluss ergodisch.^[2][3] Weiterhin ist er in diesem Fall exponentiell mischend, hat positive Entropie, dichte Orbiten, die Menge der periodischen Orbiten ist dicht und es gibt unendlich viele (linear unabhängige) invariante Maße.

Stabile und instabile Mannigfaltigkeiten

Wenn ${\displaystyle M}$ strikt negative Schnittkrümmung hat (und auch noch unter schwächeren Voraussetzungen) ist der geodätische Fluss ein Anosov-Fluss.

Beziehung zur Dynamik der Sphäre im Unendlichen

Wenn ${\displaystyle M}$ nichtpositive Schnittkrümmung hat und der geodätische Fluss nicht-wandernd ist, dann hat die Wirkung von ${\displaystyle \pi _{1}M}$ auf der Sphäre im Unendlichen ${\displaystyle \partial _{\infty }{\widetilde {M}}}$ genau dann dichte Orbiten, wenn der geodätische Fluss auf dem Einheitstangentialbündel dichte Orbiten hat.

Beispiel: Hyperbolische Ebene

Es sei ${\displaystyle H^{2}}$ die hyperbolische Ebene und ${\displaystyle T^{1}H^{2}}$ ihr Einheitstangentialbündel. Die Wirkung der Gruppe der orientierungserhaltenden Isometrien

${\displaystyle \mathrm {Isom} ^{+}(H^{2})\simeq {PSL}(2,\mathbb {R} )}$

auf ${\displaystyle T^{1}H^{2}}$ induziert eine Bijektion zwischen ${\displaystyle PSL(2,\mathbb {R} )}$ und ${\displaystyle T^{1}H^{2}}$. Wir betrachten die Wirkung von ${\displaystyle PSL(2,\mathbb {R} )}$ auf ${\displaystyle T^{1}H^{2}=PSL(2,\mathbb {R} )}$ als Links-Wirkung. Dann entspricht der geodätische Fluss ${\displaystyle \Phi _{t}}$ der Rechts-Wirkung von ${\displaystyle \left({\begin{array}{cc}e^{t}&0\\0&e^{-t}\end{array}}\right)}$ auf ${\displaystyle PSL(2,\mathbb {R} )}$. Die stabilen und instabilen Mannigfaltigkeiten des geodätischen Flusses sind die Einschränkungen des Einheitstangentialbündels auf die Horozykel, algebraisch lassen sie sich beschreiben als die Nebenklassen von ${\displaystyle N^{+}=\left\{\left({\begin{array}{cc}1&n\\0&1\end{array}}\right):n\in \mathbb {R} \right\}}$ bzw. ${\displaystyle N^{-}=\left\{\left({\begin{array}{cc}1&0\\n&1\end{array}}\right):n\in \mathbb {R} \right\}}$.

Literatur

• Patrick Eberlein: Geodesic flows in manifolds of nonpositive curvature. In: Proc. Sympos. Pure Math. Band 69, 2001, S. 525–571. (citeseerx.ist.psu.edu; PDF)

Weblinks

• Terence Tao: The Euler-Arnold equation.
• Terence Tao: Noether’s theorem, and the conservation laws for the Euler equations.

Einzelnachweise

1. ↑ V. Arnold: Sur la géométrie différentielle des groupes de Lie de dimension infinie et ses applications à l'hydrodynamique des fluides parfaits. In: Ann. Inst. Fourier. (Grenoble). Band 16, Nr. 1, 1966, S. 319–361.
2. ↑ D. V. Anosov: Geodesic flows on closed Riemannian manifolds of negative curvature. In: Trudy Mat. Inst. Steklov. Volume 90, 1967, S. 3–210. (online)
3. ↑ W. Ballmann, M. Brin: On the ergodicity of geodesic flows. In: Erg. Th. Dyn. Syst. 2, 1982, S. 311–315.