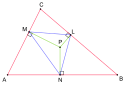
Fußpunktdreieck

Dreieck ABC (rot), Lote vom Punkt P auf die Seiten (grün), Fußpunktdreieck von P (blau)

Fußpunktdreieck ist ein Begriff aus der Dreiecksgeometrie. Sind ein Dreieck ABC und ein Punkt P gegeben, so ist das Fußpunktdreieck von P durch die Fußpunkte der drei Lote von P auf die (gegebenenfalls verlängerten) Dreiecksseiten gegeben. Liegt P auf dem Umkreis von ABC, so entartet das Fußpunktdreieck zu einer Strecke, die auf der simsonschen Geraden liegt.

Ist der gegebene Punkt P der Höhenschnittpunkt des Dreiecks, so spricht man vom Höhenfußpunktdreieck.

Die Seitenlängen eines Fußpunktdreiecks lassen sich aus den Seitenlängen des ursprünglichen Dreiecks, den Abständen von dessen Eckpunkten zum Punkt P und dem Radius r des Umkreises berechnen. Es gilt:

${\displaystyle {\begin{aligned}&|MN|&={\frac {|AP|\cdot |BC|}{2r}}\\&|NL|&={\frac {|BP|\cdot |AC|}{2r}}\\&|LM|&={\frac {|CP|\cdot |AB|}{2r}}\\\end{aligned}}}$

Diese Beziehungen gelten auch im Falle des entarteten Dreiecks, wenn P auf dem Umkreis liegt und die entsprechenden Streckenabschnitte auf der simsonschen Geraden.

Beweis

Dreieck ${\displaystyle \triangle ABC}$ mit Fußpunktdreieck ${\displaystyle \triangle LMN}$
Aufgrund des Satz des Thales ist ${\displaystyle |AP|}$ der Durchmesser des Umkreises von ${\displaystyle \triangle ANM}$, daher gilt nach dem Sinussatz: ${\displaystyle |MN|=|AP|\cdot \sin \alpha }$

Wenn das Dreieck ${\displaystyle ABC}$ die Winkel ${\displaystyle \alpha ,\beta ,\gamma }$ hat, so gilt aufgrund des erweiterten Sinussatzes:

${\displaystyle {\begin{aligned}&\sin \alpha &={\frac {|BC|}{2r}}\\&\sin \beta &={\frac {|AC|}{2r}}\\&\sin \gamma &={\frac {|AB|}{2r}}\\\end{aligned}}}$

Wendet man den Sinussatz auf die Dreiecke ${\displaystyle \triangle ANM}$, ${\displaystyle \triangle BLN}$ und ${\displaystyle \triangle CML}$ an, so gilt zudem (siehe auch Zeichnung):

${\displaystyle {\begin{aligned}&|MN|&=|AP|\cdot \sin \alpha \\&|NL|&=|BP|\cdot \sin \beta \\&|LM|&=|CP|\cdot \sin \gamma \\\end{aligned}}}$

Beides zusammen liefert dann die obigen Gleichungen.

Literatur

• J. Vályi: Über Fußpunktdreiecke. In: Monatshefte für Mathematik, Band 14, Nr. 1, Dezember 1903, Springer
• H. S. M. Coxeter, S. L. Greitzer: Geometry Revisited. MAA, 1967, S. 22–26
• M. S. Klamkin: On Pedal Triangles. In: The Mathematics Teacher, Band 91, Nr. 6, National Council of Teachers of Mathematics, 1998, S. 513–513 (JSTOR)
• S. G. Emslie: 2868. The Area of the Pedal Triangle. In: The Mathematical Gazette, Band 43, Nr. 346, Mathematical Association, 1959, S. 276–77 (JSTOR)
• Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 11, 135–144 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry)

Weblinks

• Eric W. Weisstein: Pedal Triangle. In: MathWorld (englisch).