Faserbündel
In der algebraischen Topologie, einem Teilgebiet der Mathematik, ist ein Faserbündel ein topologischer Raum, der lokal als kartesisches Produkt zweier topologischer Räume dargestellt werden kann, zusammen mit einer Abbildung, die diese Ähnlichkeit wiedergibt.
Faserbündel spielen eine wichtige Rolle in der Homotopietheorie, Differentialgeometrie und Differentialtopologie.

Geschichte
Das Konzept eines Faserbündels kam erstmals im Zusammenhang mit der Topologie und Geometrie von Mannigfaltigkeiten auf.[1] Herbert Seifert führte im Jahr 1933 die Begriffe Faser und gefaserter Raum ein.[2]
Die erste Definition eines Faserbündels gab Hassler Whitney im Jahr 1935 unter dem Namen Sphären-Raum (engl. sphere space). In den Jahren von 1935 bis 1940 wurden Faserbündel in der Mathematik ein eigenes Forschungsgebiet. Die Arbeiten von Whitney, Heinz Hopf und Eduard Stiefel gaben Ausblicke auf die Bedeutung von Faserbündeln in Topologie und Differentialgeometrie.[3]
Bis zum Jahr 1950 wurde die Definition eines Faserbündels klar notiert und die Theorie über Homotopieklassifikation und Charakteristikklassen von Faserbündeln von mehreren Mathematikern, darunter Shiing-Shen Chern, Lew Pontrjagin, Stiefel und Whitney, vorangetrieben. In den Jahren von 1950 bis 1955 konnte Friedrich Hirzebruch unter Verwendung der Charakteristikklassen von Faserbündeln den Satz von Hirzebruch-Riemann-Roch beweisen. John Milnor gab eine Konstruktion eines universellen Faserbündels für beliebige topologische Gruppen im Jahr 1955 an. In den frühen 1960ern entwickelten Alexander Grothendieck, Michael Atiyah und Hirzebruch eine verallgemeinerte Kohomologietheorie, die K-Theorie, mit Hilfe von Stabilitätsklassen von Vektorbündeln.[4]
Definition
Ein Faserbündel ist ein Quadrupel bestehend aus topologischen Räumen , und und einer stetigen surjektiven Abbildung , wobei für jedes eine offene Umgebung von und ein Homöomorphismus existieren, sodass das folgende Diagramm kommutiert:
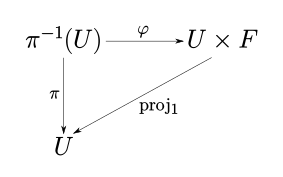
Hierbei ist die natürliche Projektion. Ein solcher Homöomorphismus wird lokale Trivialisierung des Bündels und die Abbildung Projektion genannt. Der Raum heißt der Basisraum des Bündels, der Totalraum und die Faser.
Der Raum ist mit der Produkttopologie versehen und mit der Teilraumtopologie.
Um zusätzlich die Faser des Bündels zu nennen, wird auch die Notation für ein Faserbündel verwendet. Hierbei ist die Abbildung die Inklusion und wird mit , der Faser über einem Punkt , identifiziert.[5]
Jedes Faserbündel ist eine Serre-Faserung.[6]
Beispiele
Triviales Bündel
Sei und die Projektion auf den ersten Faktor, dann ist nicht nur lokal ein Produkt, sondern auch global. Ein solches Faserbündel heißt triviales Bündel oder Produktbündel.[7]
Überlagerung
Ein Faserbündel mit diskreter Faser ist eine Überlagerung. Ebenso ist jede Überlagerung, deren Fasern alle die gleiche Kardinalität haben, ein Faserbündel mit diskreter Faser. Insbesondere ist eine Überlagerung über einem zusammenhängenden Basisraum ein Faserbündel.[8]
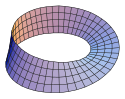
Möbiusband

Das Möbiusband ist ein anschauliches Beispiel für ein nichttriviales Faserbündel. Der Basisraum ist die Kreislinie , die mittig des Bandes verläuft. Die Faser ist durch ein abgeschlossenes Intervall gegeben, z. B.
Der Totalraum ist gegeben durch den Quotientenraum mit der Äquivalenzrelation gegeben durch Die Bündelprojektion ist die von der Projektion induzierten Abbildung, d. h., eine Äquivalenzklasse wird unter der Bündelprojektion auf die Äquivalenzklasse abgebildet, wobei die Äquivalenzrelation auf durch gegeben ist.
Das entsprechende triviale Bündel ist ein Zylinder. Möbiusband und Zylinder unterscheiden sich durch eine Verdrehung der Faser. Diese Verdrehung ist nur global sichtbar, lokal sind Möbiusband und Zylinder identisch.[9]
Kleinsche Flasche

Ein weiteres nichttriviales Faserbündel ist die Kleinsche Flasche. Der Basisraum und die Faser sind durch und der Totalraum durch den Quotientenraum gegeben, wobei die Äquivalenzrelation durch und gegeben ist. Die Bündel-Projektion bildet ein Element auf mit der Äquivalenzrelation auf ab.
Das entsprechende triviale Bündel ist ein Torus, der lokal von der Kleinschen Flasche nicht unterscheidbar ist.[10]
Hopf-Bündel
Das Hopf-Bündel hat als Faser, Totalraum und Basisraum Sphären und ist eines der ersten entdeckten nicht trivialen Faserbündel. Es ist ein Spezialfall für des Faserbündels über dem -dimensionalen komplexen projektiven Raum. Weitere Hopf-Bündel, auch verallgemeinerte Hopf-Bündel genannt, lassen sich durch Ersetzen der komplexen Zahlen durch die reellen Zahlen, die Quaternionen und die Oktonionen herleiten:
- Die Überlagerung über dem -dimensionalen projektiven Raum ergibt für das reelle Hopf-Bündel .
- Für die Quaternionen ergibt sich das Hopf-Bündel .
- Für die Oktionen ergibt sich das Hopf-Bündel .
Weitere Faserbündel, deren Faser, Totalraum und Basisraum Sphären sind, existieren nicht. Dies ist eine Folgerung aus dem Satz von Adam, welcher das Problem von Hopf über die Anzahl der Abbildungen zwischen Sphären mit Hopf-Invariante 1 löst.[11]
Schnitt
Ein globaler Schnitt eines Faserbündels ist eine stetige Abbildung , die zur Projektion rechtsinvers ist. Für alle gilt also, dass die Verknüpfung von Projektion und Schnitt gleich der Identität ist: . Anders ausgedrückt liegt für alle das Bild des Schnitts in der Faser über : .
Ein lokaler Schnitt eines Faserbündels ist eine stetige Abbildung , wobei eine offene Teilmenge ist und für alle gilt.[12]
Bündelmorphismus
Ein Bündelmorphismus (auch Bündelabbildung genannt) zwischen zwei Faserbündeln und ist eine Abbildung, die die Bündelstruktur erhält; in gewissem Sinne ist er eine Faser-erhaltende Abbildung. Genauer ist ein Bündelmorphismus durch ein Tupel von zwei Abbildungen und gegeben, sodass gilt. Die Situation wird durch das folgende kommutative Diagramm verdeutlicht:

Eine Faser über wird unter auf eine Faser über abgebildet; dies wird durch die Beziehung dargestellt.
Sind die Basisräume identisch, so ist der Bündelmorphismus durch gegeben und man spricht von einem -Morphismus oder einem Bündelmorphismus über , wobei gilt. Die Beziehung ist durch das folgende Diagramm gegeben:

Für alle gilt die Bedingung , weshalb auch Faser-erhaltend genannt wird.[13]
Koordinatenbündel
Für jeden Basisraum eines Faserbündels existiert ein Atlas von Karten, wobei offene Teilmengen und lokale Trivialisierungen des Faserbündels sind. Zwei Karten und können mittels stetiger Kartenwechsel gewechselt werden. Die Kartenwechsel geben Auskunft darüber, welche Symmetrien der Fasern beim Übergang benutzt werden, weshalb sie auch Übergangsfunktionen genannt werden. Für ein Punkt ist die Übergangsfunktion durch den Ausdruck gegeben. Das folgende Diagramm verdeutlicht die Situation:

In der ersten Zeile ist die erste Komponente durch die Identität und die zweite Komponente durch die Übergangsfunktion gegeben.[14]
Eine topologische Transformationsgruppe eines topologischen Raumes relativ zu einer Abbildung ist eine topologische Gruppe sodass:
- stetig ist
- wobei die Identität von ist und
- für alle und
Oft betrachtet man mehr als nur eine solche Abbildung und ersetzt deshalb durch [15]
Ein Koordinatenbündel ist ein Faserbündel zusammen mit einer effektiven topologischen Transformationsgruppe sodass die folgenden zwei Bedingungen gelten:
- Für jedes und entspricht der Homöomorphismus der Operation eines Gruppenelements in
- für jedes ist die Abbildung mit stetig.
Die Abbildungen heißen Koordinaten-Übergangsfunktionen (teilweise auch nur Übergangsfunktionen genannt[16]) und heißt die Strukturgruppe des Bündels. Die Koordinaten-Übergangsfunktionen haben die folgenden drei Eigenschaften:
- für jedes und jedes
- für jedes
- für jedes
Zwei Koordinatenbündel mit selbem Basisraum und Totalraum, gleicher Faser, Projektion und Strukturgruppe heißen äquivalent, wenn die Atlanten und für zwei Indexmengen und die folgenden zwei Bedingungen erfüllen:
- Für jedes stimmt mit der Operation eines Gruppenelements überein und
- die so definierten Koordinaten-Übergangsfunktionen sind stetig.
Ein -Faserbündel ist eine Äquivalenzklasse von Koordinatenbündeln. Häufig wird ein -Faserbündel auch als maximales Koordinatenbündel definiert.[17]
Der Bündelkonstruktionssatz liefert Bedingungen, unter welchen die Existenz eines Koordinatenbündels garantiert ist:
Für jede topologische Transformationsgruppe von einem Raum und System von Übergangsfunktionen in einem Raum , das heißt eine Überdeckung und eine Menge von stetigen Abbildungen mit den drei oben genannten Eigenschaften für Koordinaten-Übergangsfunktionen, existiert ein Koordinatenbündel mit Basisraum Faser Strukturgruppe und Übergangsfunktionen [18]
Hauptfaserbündel
Ein -Hauptfaserbündel ist ein Faserbündel mit Faser und einer Strukturgruppe die auf der Faser durch Linksmultiplikation operiert. Die Strukturgruppe operiert frei auf dem Totalraum durch Rechtsmultiplikation mit Bahnenraum [19]
Eine offene Überdeckung von wird abzählbar genannt, falls eine lokal endliche Zerlegung der Eins existiert:
- mit für jedes
Ein -Hauptfaserbündel heißt abzählbar, falls eine abzählbare Überdeckung von existiert, sodass die eingeschränkten Bündel für jedes triviale Bündel sind. Ein abzählbares -Hauptfaserbündel heißt universelles Bündel, falls für jeden Raum die Abbildung von der Menge der Homotopieklassen von Abbildungen von nach in die Menge der Isomorphieklassen von -Hauptfaserbündeln eine Bijektion ist. Bei einem universellen Bündel wird der Basisraum klassifizierender Raum von genannt.[20]
Hauptfaserbündel spielen eine wichtige Rolle bei der Klassifikation von Bündeln. Zudem kann jedes -Faserbündel mit einem Hauptfaserbündel assoziiert werden und umgekehrt jedes Hauptfaserbündel mit einem -Faserbündel.
Assoziierte Hauptfaserbündel
Für ein gegebenes -Faserbündel lässt sich ein -Hauptfaserbündel konstruieren. Die Existenz ist durch den Bündelkonstruktionssatz gegeben, wobei die Faser als gewählt wird und zusätzlich auf sich selbst durch Linksmultiplikation operiert. Der Basisraum und das System von Übergangsfunktionen werden identisch mit denen des -Faserbündels gewählt.[21]
Assoziierte G-Faserbündel
Für ein gegebenes -Hauptfaserbündel und einen links -Raum lässt sich ein -Faserbündel konstruieren:
Auf dem Produktraum ist eine rechts -Raum Struktur durch definiert. Das -Faserbündel ist durch die Abbildung mit und der Faser gegeben.[22]
Vektorbündel
Ein Vektorbündel vom Rang über einem Körper ist ein Faserbündel dessen Fasern die Struktur eines -dimensionalen -Vektorraumes haben und zusätzlich jede lokale Trivialisierung für ein einen -linearen Isomorphismus auf den einzelnen Fasern induziert. Das bedeutet, dass die Abbildung eingeschränkt auf ein ein Isomorphismus ist und somit gilt. Häufig betrachtet man reelle oder komplexe Vektorbündel, bei denen der Körper durch die reellen Zahlen bzw. durch die komplexen Zahlen gegeben sind.
Es gibt eine natürliche Bijektion zwischen den Isomorphieklassen von Vektorbündeln mit Rang von parakompakten Räumen und der Menge der Homotopieklassen von Abbildungen von in die Graßmann-Mannigfaltigkeit von -dimensionalen Unterräumen in [23]
Beispiele
- Das Tangentialbündel der mit Totalraum und Projektion ist ein Vektorbündel mit Fasern für jedes
- Das kanonische Vektorbündel mit Rang der Graßmann-Mannigfaltigkeit ist durch den Totalraum und die Projektion gegeben.[24]
Sphärenbündel
Ein -Sphärenbündel ist ein Faserbündel mit der -Sphäre als Faser. Oft ist ein Sphärenbündel zusammen mit der orthogonalen Gruppe als Strukturgruppe gegeben.[25]
Ein Sphärenbündel wird orientierbar genannt, falls die Strukturgruppe durch die Drehgruppe gegeben ist.[26]
Die Kohomologie von Sphärenbündeln kann mittels der Gysin-Sequenz berechnet werden.
Kohomologie von Faserbündeln
Die Bestimmung der Kohomologiegruppen von Faserbündeln ist deutlich schwieriger, als die Bestimmung der Homotopiegruppen. Die Homotopiegruppen sind durch eine lange exakte Sequenz gegeben, die Kohomologiegruppen haben dagegen nur unter bestimmten Voraussetzungen eine lange exakte Sequenz.
Für ein triviales Bündel ist die Beziehung der Kohomologiegruppen durch die Künneth-Formel gegeben. Für beliebige Faserbündel werden Hilfsmittel, wie Spektralsequenzen benötigt.
Der Satz von Leray-Hirsch liefert ausreichende Bedingungen an ein Faserbündel, sodass die Struktur der Kohomologiegruppen der eines trivialen Bündels sehr ähnlich ist.
Für -Sphärenbündel die zusätzlich eine Orientierbarkeitsbedingung erfüllen, existiert eine lange exakte Sequenz von Kohomologiegruppen. Die Sequenz ist unter dem Namen Gysin-Sequenz bekannt:
Hierbei ist eine bestimmte Eulerklasse in [27]
Beispiele
- Das Hopf-Bündel hat nicht die Kohomologiestruktur eines trivialen Bündels, da gilt.[28]
- Für das Faserbündel gilt: [29]
Einzelnachweise
- ↑ Herbert Seifert: Topologie Dreidimensionaler Gefaserter Räume. Band 60. Acta Mathematica, 1933, S. 147–238, doi:10.1007/BF02398271.
- ↑ Hassler Whitney: Sphere-Spaces. Band 21, Nr. 7. Proceedings of the National Academy of Science of the United States of America, 12. Juni 1935, S. 464–468, doi:10.1073/pnas.21.7.464, PMC 1076627 (freier Volltext).
- ↑ Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951, ISBN 0-691-08055-0. Preface
- ↑ Dale Husemoller: Fibre Bundles. Springer Verlag, Princeton NJ 1994, ISBN 0-387-94087-1. Preface
- ↑ Allen Hatcher: Algebraic Topology. Cambridge University Press, NY 2001, ISBN 0-521-79160-X, S. 376–377.
- ↑ Allen Hatcher: Algebraic Topology. Cambridge University Press, NY 2001, ISBN 0-521-79160-X, S. 379.
- ↑ Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951, ISBN 0-691-08055-0, S. 3.
- ↑ Allen Hatcher: Algebraic Topology. Cambridge University Press, NY 2001, ISBN 0-521-79160-X, S. 377.
- ↑ Allen Hatcher: Algebraic Topology. Cambridge University Press, NY 2001, ISBN 0-521-79160-X, S. 377.
- ↑ Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951, ISBN 0-691-08055-0, S. 4.
- ↑ Allen Hatcher: Algebraic Topology. Cambridge University Press, NY 2001, ISBN 0-521-79160-X, S. 377–379.
- ↑ Dale Husemoller: Fibre Bundles. Springer Verlag, Princeton NJ 1994, ISBN 0-387-94087-1, S. 11.
- ↑ Dale Husemoller: Fibre Bundles. Springer Verlag, Princeton NJ 1994, ISBN 0-387-94087-1, S. 14.
- ↑ Gerd Laures, Markus Szymik: Grundkurs Topologie. 2. Auflage. Springer Spektrum, Berlin / Heidelberg 2014, ISBN 978-3-662-45952-2, S. 184, doi:10.1007/978-3-662-45953-9.
- ↑ Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951, ISBN 0-691-08055-0, S. 7.
- ↑ James F. Davis, Paul Kirk: Lecture Notes in Algebraic Topology. 1991, S. 77–80.
- ↑ Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951, ISBN 0-691-08055-0, S. 6–9.
- ↑ Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951, ISBN 0-691-08055-0, S. 14.
- ↑ James F. Davis, Paul Kirk: Lecture Notes in Algebraic Topology. 1991, S. 84.
- ↑ Dale Husemoller: Fibre Bundles. Springer Verlag, Princeton NJ 1994, ISBN 0-387-94087-1, S. 48–50.
- ↑ Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951, ISBN 0-691-08055-0, S. 36.
- ↑ Dale Husemoller: Fibre Bundles. Springer Verlag, Princeton NJ 1994, ISBN 0-387-94087-1, S. 43–44.
- ↑ Dale Husemoller: Fibre Bundles. Springer Verlag, Princeton NJ 1994, ISBN 0-387-94087-1, S. 23.
- ↑ Dale Husemoller: Fibre Bundles. Springer Verlag, Princeton NJ 1994, ISBN 0-387-94087-1, S. 12–13.
- ↑ Edwin H. Spanier: Algebraic Topology. Springer Science & Business Media, ISBN 978-0-387-94426-5, S. 91, doi:10.1007/978-1-4684-9322-1.
- ↑ Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951, ISBN 0-691-08055-0, S. 34.
- ↑ Allen Hatcher: Algebraic Topology. Cambridge University Press, NY 2001, ISBN 0-521-79160-X, S. 438.
- ↑ Allen Hatcher: Algebraic Topology. Cambridge University Press, NY 2001, ISBN 0-521-79160-X, S. 432.
- ↑ Allen Hatcher: Algebraic Topology. Cambridge University Press, NY 2001, ISBN 0-521-79160-X, S. 434.
Weblinks
Auf dieser Seite verwendete Medien
Autor/Urheber: Julian Nill, Lizenz: CC BY-SA 4.0
Das Diagramm zeigt einen Bündelmophismus
Autor/Urheber: Julian Nill, Lizenz: CC BY-SA 4.0
Das Diagramm zeigt einen Bündelmorphismus für identische Basisräume
Autor/Urheber: Krishnavedala, Lizenz: CC BY-SA 3.0
This immersion of the Klein bottle into R3 is given by the following parameterization. Here the parameters u and v run from 0 to 2π and r is a fixed positive constant (=1 in this figure).
For :
For :
лента мёбиуса
Autor/Urheber: Julian Nill, Lizenz: CC BY-SA 4.0
Das Diagramm zeigt den Kartenwechsel eines Faserbündels
Autor/Urheber: IkamusumeFan, Lizenz: CC BY-SA 4.0
The local triviality of fibre bundles.