Evolventenverzahnung

Abb. 1: Entstehung einer Evolvente

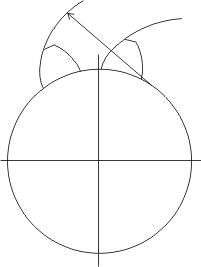
Die Evolventenverzahnung ist eine von mehreren Verzahnungsarten für Zahnräder. Sie ist die bedeutendste Verzahnungsart im Maschinenbau.

Die Evolventenform erfüllt die geometrischen Anforderungen an die Zahnflankengeometrie aus dem Verzahnungsgesetz:

Die gemeinsame Normale (Senkrechte) der beiden Zahnprofile (Kurven) geht in jedem möglichen Berührungspunkt immer durch den Wälzpunkt C (siehe Abbildung 3), der die Verbindungslinie zwischen den Drehpunkten der beiden Zahnräder im umgekehrten Verhältnis der Winkelgeschwindigkeiten teilt.

Grundbegriffe

Bezeichnungen

Abb. 2: Wichtigste Bezeichnungen eines Stirnrades

${\displaystyle d_{a}}$: Kopfkreisdurchmesser

${\displaystyle d}$: Teilkreisdurchmesser

${\displaystyle d_{b}}$: Grundkreisdurchmesser

${\displaystyle d_{f}}$: Fußkreisdurchmesser

${\displaystyle d_{w}}$:Wälzkreisdurchmesser

${\displaystyle h_{aP}}$: Kopfhöhe

${\displaystyle h_{fP}}$: Fußhöhe

${\displaystyle s}$: Zahndicke (am Teilkreis)

${\displaystyle e}$: Zahnlücke (am Teilkreis)

${\displaystyle p}$: Teilung (am Teilkreis) mit ${\displaystyle p=s+e}$

${\displaystyle z}$: Anzahl der Zähne

${\displaystyle x}$: Profilverschiebungsfaktor (ohne Einheit)

${\displaystyle x\cdot m}$: Profilverschiebung (in mm)

In der Skizze hat das hellgrau dargestellte Zahnrad eine positive Profilverschiebung.

Bezugsprofil

Das Bezugsprofil entspricht dem theoretischen Zahnstangenprofil, auf dem das Zahnrad spielfrei abwälzt. In der Praxis ist es die Form des Werkzeugs, mit dem das Zahnrad im Wälzfräsverfahren hergestellt wird.

Das Bezugsprofil heute gebräuchlicher Zahnräder ist in DIN 867 genormt.

Modul

Der Modul (Formelzeichen m, Einheit mm) ist die wichtigste Bezugsgröße bei Evolventenverzahnungen. Alle Abmessungen des Bezugsprofils werden als Faktoren des Moduls angegeben, was durch ein Sternchen (*) im Variablennamen gekennzeichnet wird. Beträgt beispielsweise der Fußhöhenfaktor (h_fP*) des Zahnes 1,2, so ergibt sich bei einem Modul von 2 mm eine Fußhöhe von 2,4 mm. Der Modul gibt gewissermaßen die Größenkategorie der Zähne an; Zahnräder unterschiedlicher Größe mit gleichem Modul können miteinander gepaart werden. Verändert man bei einem Zahnrad nur den Modul und behält die anderen Faktoren bei, so erhält man demnach ein geometrisch ähnliches Zahnrad. Daraus ist zu erkennen, dass auch der Zahnraddurchmesser proportional zum Modul ist, über den Zusammenhang:

${\displaystyle m={\frac {d}{z}}={\frac {p}{\pi }}}$

Abwälzung

Abb. 3: Zahneingriff eines Stirnradpaares

Der Berührpunkt zweier Zahnflanken bewegt sich während des gesamten Eingriffs auf einer Geraden, der Eingriffsstrecke AE (siehe Abbildung 3). Den Winkel, um den die Eingriffsstrecke geneigt ist, nennt man Eingriffswinkel. Dieser entspricht dem Flankenwinkel des Bezugsprofils (gilt nur ohne Profilverschiebung). Üblich sind hierbei 20°, wobei es vor allem in der Feinwerktechnik auch Zahnräder mit bis zu 5° Eingriffswinkel (Hochverzahnungen) gibt. In Fahrzeuggetrieben werden häufig aus Geräuschgründen (längere Eingriffsstrecke und damit größere Profilüberdeckung) Bezugsprofile mit einem Profilwinkel von 17,5° eingesetzt. Größere Eingriffswinkel ergeben zwar im Allgemeinen eine höhere Zahnfußtragfähigkeit, sind bei zu großen Werten (>30°) aber nur bedingt sinnvoll, weil sich dadurch die Eingriffsstrecke erheblich verkürzt, was im Allgemeinen im Hinblick auf die Laufruhe nachteilig ist.

Während der Berührpunkt auf der Eingriffsstrecke entlangwandert, variiert die Gleitgeschwindigkeit der Zähne zueinander. Vom Standpunkt des treibenden Zahnrads aus herrscht am Anfang des Eingriffs schiebendes Gleiten vor, das bis zur Mitte der Eingriffsstrecke hin abnimmt. Im so genannten Wälzpunkt C (auch Berührpunkt beider Wälzkreise d_w), wird die Gleitgeschwindigkeit zu Null. Der Wälzpunkt C liegt nicht wie häufig behauptet im Mittelpunkt der Eingriffsstrecke, sondern befindet sich im Schnittpunkt zwischen Eingriffslinie und Mittellinie der Zahnradachsen^[1]. In diesem Punkt liegt reines gleitfreies Abwälzen vor. In der zweiten Hälfte der Eingriffsstrecke steigt die Gleitgeschwindigkeit in ziehender Bewegungsrichtung wieder an. Die Vorzeichen der Geschwindigkeiten sind für das angetriebene Zahnrad dementsprechend vertauscht.

Die Gleitrichtungsumkehr am Wälzpunkt kann durch den sog. Reibwechselstoß eine Geräuschursache darstellen.

Profilverschiebung

Unter einer Profilverschiebung versteht man, dass der Abstand des herstellenden Werkzeugs zum Zahnrad vergrößert oder verkleinert wird. Der Profilverschiebungsfaktor trägt das Formelzeichen x und gibt die auf den Normalmodul bezogene radiale Verschiebung des Werkzeuges an (siehe Abbildung 2), wobei bei Außenverzahnungen ein positiver Wert eine Verschiebung vom Zahnradmittelpunkt weg bedeutet und ein negativer Wert eine Verschiebung zum Mittelpunkt hin bedeutet.

Vorteile

Die blaue Pfeile zeigen die Kontaktkräfte zwischen den Zahnflanken am Kontaktpunkt. Die Kraft verläuft entlang einer Tangente, die beiden Grundkreisen gemeinsam ist.

Konstante Drehwinkelübertragung

Bei Verzahnungsauslegung nach dem Verzahnungsgesetz, richtiger Fertigung und Montage der Evolventenverzahnung befindet sich immer mindestens ein Zahnpaar im Eingriff. Dadurch erlaubt die Evolventenverzahnung in der Theorie die gleichmäßige Übertragung von Drehwinkeln durch eine konstante Übersetzung.

In der Praxis jedoch können aufgrund der wechselnden Eingriffsverhältnisse (momentaner Kraftangriffspunkt am Zahn und momentane Profilüberdeckung) Drehschwingungen auftreten, die zu Geräuschen führen können.

Zur Steigerung der übertragbaren Drehmomente und zur Verbesserung der Laufruhe wird versucht, möglichst viele Zahnpaare gleichzeitig an der Drehmomentübertragung zu beteiligen.

Dies ist z. B. auch mithilfe von Schrägverzahnung möglich, bei der sich zu der Profilüberdeckung noch die Sprungüberdeckung zur resultierenden Gesamtüberdeckung addiert.

Konstante Drehmomentübertragung

Bei Vernachlässigung der auftretenden Gleitreibung im Zahneingriff ist die Drehmomentübertragung konstant. Diese Betrachtungsweise ist in vielen Anwendungsfällen ausreichend.

In speziellen Anwendungen kann dies jedoch nicht vernachlässigt werden.

Wie bereits weiter oben unter Abwälzung beschrieben, beginnt der Zahneingriff mit schiebendem Gleiten bei abnehmender Geschwindigkeit bis zum Wälzpunkt (C), das dort seine Richtung in ziehendes Gleiten bei zunehmender Geschwindigkeit bis zum Zahnaustritt umkehrt. Da die Reibungsverluste in der Verzahnung von der jeweiligen Gleitgeschwindigkeit abhängig sind, ändern sich diese während eines Zahneingriffs. Und die Energie, die in der Verzahnung durch Reibung verloren geht, kann am Abtrieb nicht ankommen. Somit kann die Drehmomentübertragung nicht vollkommen gleichmäßig sein.

In manchen Anwendungen ist dieser Effekt unerwünscht, z. B. bei hoch ins Schnelle übersetzenden, evtl. mehrstufigen Getrieben, wie beispielsweise mechanischen Uhrwerken. Ein am Antrieb während eines Zahneingriffs anliegendes konstantes Drehmoment (aus Feder oder Gewicht) würde beim Gangregler (Pendel oder Unruh) in längeren Perioden stark schwankend ankommen und damit die Ganggenauigkeit der Uhr^[2][3][4][5] herabsetzen.

Deshalb werden hier meist andere Flankenformen bevorzugt.  

Achsabstandstoleranz

Die Evolventenverzahnung ist im Gegensatz zu anderen Verzahnungsarten in Grenzen und bezüglich Drehwinkelübertragung unempfindlich gegen Veränderungen des Achsabstandes der beiden Zahnräder zueinander. Lediglich Eingriffswinkel und Überdeckung ändern sich dabei.

Einfache Herstellbarkeit und Kombinierbarkeit

Die Evolventenverzahnung eignet sich zur Herstellung im Wälzfräsverfahren.

Da das Bezugsprofil gerade Flanken besitzt, haben auch die zur Fertigung der Verzahnung eingesetzten Wälzfräser gerade Flanken und sind dadurch einfach herzustellen. Das Bezugsprofil üblicher Zahnräder ist in DIN 867 genormt.

Literatur

• Gustav Niemann, Hans Winter: Maschinenelemente. Band 2: Getriebe allgemein, Zahnradgetriebe – Grundlagen, Stirnradgetriebe. 2., völlig neubearbeitete Auflage, 2., berichtigter Nachdruck. Springer, Berlin u. a. 1989, ISBN 3-540-11149-2.

Einzelnachweise

1. ↑ tec-science: Eingriff von Evolventenzahnräder. In: tec-science. 31. Oktober 2018, abgerufen am 21. Oktober 2019 (deutsch). 
2. ↑ Gustav Niemann, Hans Winter,: Maschinenelemente. 2. überarbeitete Auflage. Band, Nr. 2. Springer, Berlin 1989, ISBN 3-540-11149-2. 
3. ↑ A. K. Thomas: Grundzüge der Verzahnung. Carl Hanser, München 1957. 
4. ↑ Karlheinz Roth: Zahnradtechnik. Band, Nr. 1. Springer, Berlin / Heidelberg / New York 1989, ISBN 3-540-51168-7. 
5. ↑ DIN 21772:2012-07 Allgemeine Begriffe und Bestimmungsgrößen für Zahnräder, Zahnradpaare und Zahnradgetriebe. Beuth Verlag, Berlin Köln Juli 2012.