Eulerscher Polyedersatz

 Der uns vertraute Würfel mit 8 Ecken, 12 Kanten und 6 Flächen erfüllt mit den Eulerschen Polyedersatz
Der uns vertraute Würfel mit 8 Ecken, 12 Kanten und 6 Flächen erfüllt mit den Eulerschen PolyedersatzDer Eulersche Polyedersatz (auch: die Eulersche Polyederformel), benannt nach Leonhard Euler, beschreibt eine fundamentale Eigenschaft von beschränkten, zur Sphäre homöomorphen Polyedern[1] bzw. allgemeiner: von zusammenhängenden planaren Graphen.
Hinter der Formel steckt das topologische Konzept der Euler-Poincaré-Charakteristik . Die Eulersche Polyederformel ist der Spezialfall für (drei Dimensionen) unter stillschweigender Vernachlässigung von (wir betrachten immer einen Körper) und ergibt dann ein :
- ( nach Eulerschem Polyedersatz)
- ( nach Euler-Poincaré-Charakteristik)
mit Anzahl der Ecken, Anzahl der Kanten, Anzahl der Flächen und Anzahl der Zellen.
Sie gilt (da so definiert) allgemein für Polyeder der Charakteristik (bzw. ), zu denen ausnahmslos alle konvexen und viele „gutmütige“ konkave Polyeder gehören, siehe dazu Abschnitt Gültigkeit.[2]
Allgemein

Der Satz besagt:
- Sind die Anzahl der Ecken, die Anzahl der Kanten und die Anzahl der Flächen eines beschränkten konvexen Polyeders, dann gilt:
Oder in Worten:
- Anzahl der Ecken minus Anzahl der Kanten plus Anzahl der Flächen gleich zwei.
Er wurde 1750 von Euler aufgeschrieben und 1758 in Latein als „Elementa doctrine solidorum“ veröffentlicht. Im Euler-Archiv[3] ist die Publikation unter dem Eneström-Index E 230, der unvollständige Beweis unter E 231 zu finden.
In Bezugnahme auf das topologische Problem (es sind keine Polyeder notwendig) und der Darstellung als planarer Graph kann der Satz auch als
- Ist die Kugeloberfläche durch ein Kurvennetz derart zerlegt, dass durch kreuzungsfreies(!) Verbinden von Eckpunkten Kurvenstücke und Flächenstücke entstehen, dann gilt:
geschrieben werden.
In der folgenden Tabelle wird die Gültigkeit für einige Polyeder, darunter die fünf platonischen Körper, mit den zugehörigen Werten für , und gezeigt.
| Polyeder | E | K | F | E − K + F |
|---|---|---|---|---|
| Dreieckskuppel | 9 | 15 | 8 | 2 |
| Trigondodekaeder | 8 | 18 | 12 | 2 |
| Pseudo-Rhombenkuboktaeder | 24 | 48 | 26 | 2 |
| Großes Rhombenikosidodekaeder | 120 | 180 | 62 | 2 |
| Tetraeder | 4 | 6 | 4 | 2 |
| Würfel | 8 | 12 | 6 | 2 |
| Oktaeder | 6 | 12 | 8 | 2 |
| Dodekaeder | 20 | 30 | 12 | 2 |
| Ikosaeder | 12 | 30 | 20 | 2 |
Gültigkeit
Der Eulersche Polyedersatz gilt für alle konvexen Polyeder. Die Konvexität ist eine zu starke Bedingung:
- Das Hineindrücken einer Ecke des Ikosaeders ändert weder Ecken-, Kanten- noch die Flächenzahl, die Konvexität spielt daher keine Rolle.
- Selbst das Durchstoßen einer Ecke durch eine andere Fläche ändert nichts daran, solange man die nur in der Geometrie entstehenden Schnittpunkte und Schnittlinien ignoriert.
- Es ist auch kein Polyeder erforderlich, da gekrümmte Flächen und gekrümmte Kanten keinen Einfluss haben, solange die Vernetzung sich nicht ändert.
- In der Topologie gibt es im Gegensatz zur Geometrie den Begriff der Konvexität nicht. Die Lage spielt keine Rolle, nur deren Verbindungen.
Sie schließt aber zuverlässig alle Fälle aus, die zu einer Verletzung des Eulerschen Polyedersatzes führen.

Zu Abweichungen führt:
- Fehlende Kreuzungsfreiheit bzw. fehlende eindeutige Orientierung von Flächen.
- Das Gesamt-Polyeder darf räumlich nicht aus zwei oder mehr separaten Einzel-Polyedern bestehen, die sich nur in einer Ecke oder an einer Kante berühren. Sonst erhöht sich um . In der allgemeineren Form als Euler-Poincaré-Charakteristik stellt dies kein Problem dar, da sich gleichzeitig auch die Anzahl der Zellen um erhöht, somit gilt dann wieder .
- Das Netzwerk aus Ecken und Kanten muss topologisch zusammenhängend sein, d. h., es muss ein gemeinsamer Graph entstehen. Weitere Graphen erhöhen um oder anders betrachtet: gilt jeweils für jeden Graphen getrennt.
- Das Polyeder darf keine „Löcher“ bzw. „Henkel“ enthalten, muss also das topologische Geschlecht haben. Jedes Loch reduziert um (wenn das Polyeder aus orientierbaren Flächen besteht), sonst um .
Gleichen sich diese Fehler exakt aus, kann wiederum der Eulersche Polyedersatz erfüllt werden, wie z. B. bei einem Würfel mit einem Quader als eingestanztem Loch (16 Ecken, 24 Kanten, 10 Flächen).
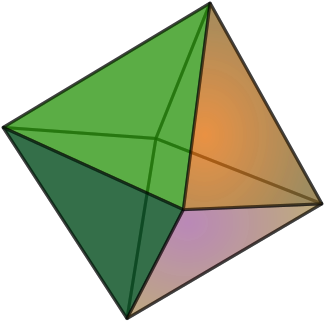
 Das konkave Tetrahemihexaeder mit 6 Ecken, 12 Kanten, aber nur 7 Flächen verletzt mit den Eulerschen Polyedersatz. Die 3 inneren, gelben Quadrate kreuzen sich und haben keine definierten Innen- und Außenseiten mehr. Der Körper ist homöomorph zur Steinerschen Fläche. Er lässt sich nicht mehr als planarer Graph darstellen.
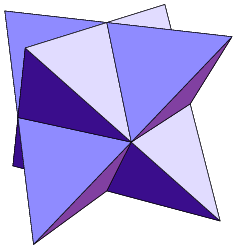
Das konkave Tetrahemihexaeder mit 6 Ecken, 12 Kanten, aber nur 7 Flächen verletzt mit den Eulerschen Polyedersatz. Die 3 inneren, gelben Quadrate kreuzen sich und haben keine definierten Innen- und Außenseiten mehr. Der Körper ist homöomorph zur Steinerschen Fläche. Er lässt sich nicht mehr als planarer Graph darstellen. Das konkave Sterntetraeder mit 14 Ecken, 36 Kanten und 24 Flächen erfüllt wiederum mit den Eulerschen Polyedersatz.
Das konkave Sterntetraeder mit 14 Ecken, 36 Kanten und 24 Flächen erfüllt wiederum mit den Eulerschen Polyedersatz. Das konkave Szilassi-Polyeder mit einem „Loch“ () mit 14 Ecken, 21 Kanten und 7 Flächen verletzt mit den Eulerschen Polyedersatz.
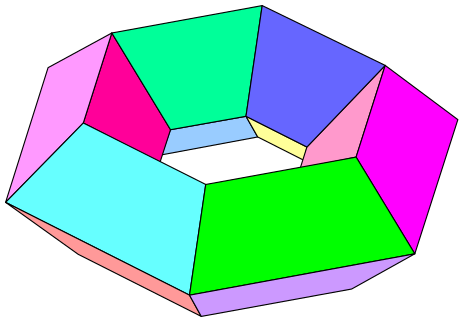
Das konkave Szilassi-Polyeder mit einem „Loch“ () mit 14 Ecken, 21 Kanten und 7 Flächen verletzt mit den Eulerschen Polyedersatz. Ein „Polyeder-Donut“ mit 30 Ecken, 60 Kanten und 30 Vierecken als Flächen verletzt mit den Eulerschen Polyedersatz.
Ein „Polyeder-Donut“ mit 30 Ecken, 60 Kanten und 30 Vierecken als Flächen verletzt mit den Eulerschen Polyedersatz. Dieses konkave Polyeder hat 32 Ecken, 90 Kanten und 60 Flächen und erfüllt mit den Eulerschen Polyedersatz. Allerdings …
Dieses konkave Polyeder hat 32 Ecken, 90 Kanten und 60 Flächen und erfüllt mit den Eulerschen Polyedersatz. Allerdings … … weist der auf den ersten Blick gleich aussehende Dodekaederstern als Kepler-Poinsot-Körper nur 12 Ecken (golden markiert, die anderen 20 sind nur Schnittpunkte der Kanten), 30 Kanten (die durch die 20 Schnittpunkte jeweils dreigeteilt werden) und 12 Flächen (Pentagramme, die in jeweils 5 Dreiecke zerfallen) auf und verletzt mit den Eulerschen Polyedersatz.
… weist der auf den ersten Blick gleich aussehende Dodekaederstern als Kepler-Poinsot-Körper nur 12 Ecken (golden markiert, die anderen 20 sind nur Schnittpunkte der Kanten), 30 Kanten (die durch die 20 Schnittpunkte jeweils dreigeteilt werden) und 12 Flächen (Pentagramme, die in jeweils 5 Dreiecke zerfallen) auf und verletzt mit den Eulerschen Polyedersatz.

Unterschied zwischen Oktaeder und Tetrahemihexaeder
Beide haben die gleiche Eckenzahl und Kantenzahl. Allerdings stellt das Flächenmodell des Tetrahemihexaeders keinen kreuzungsfreien planaren Graphen mehr dar.
- Wir sehen jeweils die 6 Ecken und die 12 Kanten beider Körper.
- Die Flächen des Oktaeders sind die 4 rötlichen und die 4 bläulichen Flächen (davon ist eine die Außenfläche).
- Die Flächen des Tetrahemihexaeder sind die 4 rötlichen Flächen (entsprechen den roten Flächen im rotierenden Modell) sowie 3 weitere zusammengesetzte Flächen (entsprechen den gelben Flächen im rotierenden Modell), die keinen einfachen Gebieten des Graphen mehr entsprechen. Dazu nehme man sich jeweils eine der 6 Ecken und folge den vier Kanten dieser Ecke zu den mit dieser Ecke direkt verbundenen Ecken. Dies sind die jeweils 4 Eckpunkte der 3 Quadrate mit jeweils den beiden möglichen Orientierungen (die Flächen haben keine Innen- und keine Außenseite mehr), die die 3 weiteren Flächen bilden.
Geschichte
Euler erwähnte den Satz zuerst in einem Brief an Christian Goldbach 1750 und veröffentlichte 1758 einen Beweis,[4] allerdings enthielt dieser nach den heutigen Maßstäben für die Strenge mathematischer Beweise einen Fehler, worauf Henri Lebesgue 1924 hinwies. Später wurde bekannt, dass der Satz schon René Descartes bekannt war (unveröffentlicht),[5] weshalb er in der französischen Literatur auch als „Satz von Descartes und Euler“ bezeichnet wird. Der Beweis von Euler benutzt die Zerlegung eines Polyeders in Tetraeder, wobei eine Ecke nach der anderen beseitigt wird.[6] Der erste strenge Beweis wurde von Adrien-Marie Legendre 1794 veröffentlicht, in seinem Buch Élements de Géométrie. Legendres Beweis benutzt die Flächenformel eines geodätischen Dreiecks auf der Kugeloberfläche. Einen korrekten Beweis fand auch Augustin Louis Cauchy 1811, veröffentlicht 1813.[7] Bis heute sind viele verschiedene Beweise bekannt.
Eine Verallgemeinerung auf -dimensionale Polyeder fanden Ludwig Schläfli und Henri Poincaré (1895). Poincaré erkannte auch die volle topologische Bedeutung des Satzes.
Beweise
Klassischer Beweis
Dieser Beweis zeigt mit struktureller Induktion die Gültigkeit des Satzes für planare Graphen.
Der einfachste planare Graph besteht aus nur einer Ecke. Es gibt eine Fläche (die Außenfläche) und keine Kanten. Es gilt also . Aus diesem einfachsten Graphen können alle weiteren ausschließlich durch die beiden folgenden Operationen konstruiert werden, welche die Gültigkeit des Satzes nicht verändern:
- Hinzufügen einer Ecke, die über eine neue Kante mit dem Rest des Graphen verbunden ist. Die Anzahl der Ecken und Kanten steigt jeweils um , während die Anzahl der Flächen gleich bleibt. Galt für den alten Graphen , so gilt es auch für den neuen, da in der Klammer der Gleichung und jeweils um erhöht werden.
- Hinzufügen einer Kante, die zwei bereits bestehende Ecken verbindet. Während die Anzahl der Ecken gleich bleibt, steigt die Anzahl der Kanten und Flächen jeweils um . Wieder bleibt die Summe gleich, da in der Klammer der Gleichung und jeweils um erhöht werden.
Da der Satz für den ersten, einfachsten Graphen galt, muss er auch für jeden Graphen gelten, der durch eine der beiden Operationen aus diesem entsteht. Jeder Graph, der durch eine weitere Operation aus einem solchen Graphen entsteht, muss den Satz ebenfalls erfüllen usw. Daher gilt der Satz für alle planaren Graphen und damit auch für alle konvexen Polyeder.
Der Beweis stammt von Augustin-Louis Cauchy. Er war der Erste, der das Problem auf ein solches der Graphentheorie reduzierte.[8]
Beweis nach von Staudt
Karl von Staudt gab 1847 einen einfachen, nichtrekursiven Beweis in seiner Geometrie der Lage.[9]
Dazu betrachte man den Graphen der planaren Projektion des Polyeders, das Knoten, Kanten und Flächen hat. Der Graph ist für die betrachteten Polyeder zusammenhängend[10] und hat damit einen Spannbaum . Da genau Knoten enthält und ein zusammenhängender Baum ist (ohne Zykel), hat er Kanten. Man betrachte nun den zu dualen Graphen , gebildet aus den Mittelpunkten der Flächen von , und verbinde diese so mit Kanten, dass diese die Kanten in nicht schneiden. Dieser Kantenzug ist zusammenhängend, da keine Kreise enthält. Er ist ebenfalls ein Baum, sonst würde er einen Kreis (Zykel) enthalten, der die Knoten von in zwei Teile teilt und somit eine Kante von schneidet, entgegen der Konstruktionsvoraussetzung. hat damit Knoten und Kanten. Die Kanten in setzen sich aus den Kanten von zusammen oder werden von einer Kante von gekreuzt, somit gilt .
Ein ungewöhnlicher Beweis

Dieser Beweis zeigt die Gültigkeit des Satzes für planare Graphen mit Hilfe des Satzes von Pick. Umgekehrt lässt sich auch der Satz von Pick aus dem Eulerschen Polyedersatz herleiten, sodass beide äquivalent sind.[11]
Um den Satz von Pick anwenden zu können, muss der Graph in ein Gitternetz eingebettet werden, sodass die Knotenpunkte des Graphen auf Gitterpunkten liegen. Der Graph bleibt äquivalent, wenn man jeden Knotenpunkt innerhalb einer geeignet kleinen Umgebung bewegt. Der Radius des kleinsten Kreises um einen Knotenpunkt, der vollständig in die Umgebung eingebettet ist, sei . Es wird ein beliebiges Gitternetz mit Einheit auf der Ebene betrachtet. Dann können wir jeden Knotenpunkt auf einen Gitterpunkt verschieben und erhalten sicher einen äquivalenten Graphen. Der planare Graph besitzt jetzt insgesamt Knotenpunkte, Kanten und innere Flächen.
Der gesamte (innere) Flächeninhalt des planaren Graphen kann mit Hilfe des Satzes von Pick auf zwei Arten bestimmt werden. Beide Berechnungen müssen das gleiche Ergebnis liefern. Wir werden diese Berechnungen ((1) und (2)) am Ende gleichsetzen und den Eulerschen Polyedersatz erhalten.
Zunächst müssen alle Gitterpunkte innerhalb des Graphen oder auf ihm charakterisiert werden:
| Inneres | Rand | Formel für A | |||||
|---|---|---|---|---|---|---|---|
| z | y | v | x | u | A | ||
| Gesamter Graph | 57 | 8 | 4 | 2 | 4 | 71 | |
| F1 (o. r.) | 17 | 4 | 2 | 0 | 2 | 20 | Bei dieser Summe liegen die Punkte und auf dem Rand. |
| F2 (o. l.) | 14 | 3 | 2 | 1 | 2 | 17 | |
| F3 (mittlere) | 11 | 2 | 4 | 0 | 0 | 13 | |
| F4 (u. r.) | 8 | 4 | 2 | 0 | 2 | 11 | |
| F5 (u. l.) | 7 | 3 | 2 | 1 | 2 | 10 | |
| Summe F1−5 | 57 | 16 | 12 | 2 | 8 | 71 | |
- Die Punkte innerhalb werden in drei Kategorien eingeteilt: Knotenpunkte , Punkte auf Kanten und sonstige .
- Die Punkte auf dem Rand werden in zwei Kategorien eingeteilt: Knotenpunkte und Punkte auf Kanten .
- Die Anzahl der Punkte sei jeweils: .
- Die Anzahl der Ecken (bzw. Knoten) ist offensichtlich die Summe derer im Inneren und derer auf dem Rand:
- . (1)
Betrachten wir nun den Graphen nur anhand seiner belegten Flächen unter Vernachlässigung seiner genauen inneren Struktur.
- Der Flächeninhalt des gesamten Graphen ist gleich der Summe der Flächeninhalte der Teilflächen:
- .
- Für die Gesamtfläche sind , und innere Punkte und und Randpunkte.
- Für die Teilflächen sind innere Punkte und , , und Randpunkte. und werden für die Teilflächen zu Randpunkten.
- Die Flächeninhalte berechnen sich daher unter Anwendung des Satzes von Pick zu:
- und
- .
- Daraus folgt:
- und ausgeschrieben
- .
- und
- Die sonstigen Punkte kommen in beiden Summen je einmal vor, daher gilt:
- .
- Gleiches gilt für die Gitterpunkte auf dem äußeren Rand , daher gilt:
- .
- Die inneren Punkte auf den Kanten kommt in der Gesamtsumme einmal vor, in der Summe der Teilsummen zweimal, da sie von beiden angrenzenden Flächen je einmal aufsummiert werden. Daher gilt:
- .
- Das ergibt:
- .
- .
- .
- Wir addieren zu beiden Seiten und bringen auf die linke Seite:
- . (2)
- Die inneren Knotenpunkte werden bei dieser Summation genau so oft gezählt wie die Anzahl der Flächen, die in diesen Knotenpunkten enden, angibt. Allerdings ist diese identisch mit der Anzahl der dort jeweils beginnenden Kanten.
- stellt damit die Anzahl der Kantenanfänge durch die inneren Knotenpunkte dar.
- Die Rand-Knotenpunkte werden bei dieser Summation um weniger gezählt als dort Flächen enden. Addiert man zu der Summe die Anzahl der Rand-Knotenpunkte dazu, ist dieser Makel beseitigt.
- stellt damit die Anzahl der Kantenanfänge durch die äußeren Knotenpunkte dar.
- Die Summe beider Ausdrücke stellt daher selbst die Anzahl aller Kantenanfänge dar.
- Da aber jede Kante zwei Kantenanfänge hat, haben Kanten Kantenanfänge. Diese Summe beträgt daher , da sie alle Kantenanfänge zählt (unabhängig davon, ob sie bei der „Planierung“ des Polyeders gerade innere oder Rand-Knotenpunkte geworden sind) und die Anzahl aller Kantenanfänge den Wert hat.
- .
- Das setzen wir in (2) ein:
- .
- Wir setzen noch (1) ein und erhalten
- bzw. . ∎
- Hinweis
Man kann den Beweis auch anhand des Beispiels numerisch Schritt für Schritt durchrechnen. Das erleichtert das Verständnis.
Verallgemeinerung auf planare Graphen
Vom Polyeder zum planaren Graphen
Hat ein Polyeder ein zusammenhängendes Inneres ohne Löcher, kann die Beziehung seiner Flächen, Kanten und Ecken auch als planarer Graph (ein ebenes, zusammenhängendes Netz, dessen Kanten einander nicht schneiden) dargestellt werden. Man bezeichnet diesen Graphen auch als Schlegeldiagramm.
Dies kann man sich wie folgt veranschaulichen: Entfernt man eine Fläche des Polyeders und zieht die angrenzenden Kanten auseinander, kann man das Netz des Polyeders auf eine Ebene projizieren und in einen planaren Graphen überführen. Dabei bleiben nicht unbedingt alle Regelmäßigkeiten des Polyeders erhalten – die entstehenden Flächen müssen noch nicht einmal Vielecke sein –, die Anzahl der Ecken, Kanten und Flächen (die Außenfläche mitgezählt) sowie die Struktur des Netzes bleiben aber erhalten.
Der Eulersche Polyedersatz für planare Graphen
Für zusammenhängende planare Graphen kann eine verallgemeinerte Version des Eulerschen Polyedersatzes formuliert werden. Dort ersetzen die Gebiete die Flächen und es gilt
- Knotenzahl Kantenzahl Gebietszahl ,
wobei bei der Gebietszahl das äußere Gebiet mitgezählt wird.
Diese Formulierung erweitert den Gültigkeitsbereich des Satzes um eine Vielzahl nichtkonvexer Polyeder sowie solcher planarer Graphen, denen überhaupt keine Polyeder zugrunde liegen.
Wird der Eulersche Polyedersatz zuerst für planare Graphen bewiesen, so ergibt sich der klassische Polyedersatz hieraus als Spezialfall.
Die Euler-Charakteristik
Eine weiterreichende Verallgemeinerung des Konzepts findet sich in der Euler-Charakteristik einer geschlossenen Fläche. Aus dieser Sichtweise ist die Konvexität des Polyeders lediglich eine (starke) hinreichende Voraussetzung, um zu gewährleisten, dass die Oberfläche des Polyeders homöomorph zur 2-Sphäre (Kugeloberfläche) ist.
Verallgemeinerung für beliebige Polytope
Der Eulersche Polyedersatz, der für dreidimensionale, zu kreuzungsfreien und zusammenhängenden Graphen homöomorphe Polyeder gilt, lässt sich für beliebige Polytope verallgemeinern:
Die statt der (im Eulerschen Polyedersatz) ergibt sich dadurch, dass das Polytop in seiner höchsten Dimension als selbst mitgezählt wird:
- Hexaeder hat Flächen, Kanten und Ecken.
Man könnte auch schreiben für ungerade und für gerade und man wäre damit näher an der Darstellung nach Euler dran, aber diese Art der Darstellung ist zum einen zweifellos unschöner und versagt des Weiteren bei Polytopen, die nicht komplett zusammenhängen. Sie dazu auch in der Einleitung die Bemerkungen zu und .
Dabei haben die Zeichen folgende Bedeutung:
- ist die Euler-Poincaré-Charakteristik des Polytops .
- ist die Dimension des Polytops , z. B.
- : Polygon wie z. B. das Quadrat,
- : Polyeder wie z. B. der Würfel und
- : Polychor wie z. B. das Tesserakt.
- : Polyeder wie z. B. der Würfel und
- ist die Anzahl der Ecken von (die Anzahl der „Begrenzungselemente“ ohne Dimension, d. h. Punkte, engl. Vertex),
- ist die Anzahl der Kanten von (die Anzahl der eindimensionalen „Begrenzungselemente“, d. h. Linien, engl. Edge),
- ist die Anzahl der Flächen von (die Anzahl der zweidimensionalen „Begrenzungselemente“, d. h. Flächen, engl. Face),
- ist die Anzahl der Zellen von (die Anzahl der dreidimensionalen „Begrenzungselemente“, d. h. Volumina, engl. Cell),
- …,
- ist die Anzahl der -Polytope (die Anzahl der -dimensionalen „Begrenzungselemente“),
- …,
- (die Anzahl der höchstdimensionalen „Begrenzungselemente“, engl. Peak, Ridge/Subfacet und Facet),
- (, wenn komplett zusammenhängend, sonst größer) zählt das Polytop selbst.
- ist die Dimension des Polytops , z. B.
Beispiele
| Polytop | Schläfli- Symbol | Ecken | Kanten | Flächen | Zellen | | | | | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0-Polytop | ||||||||||||||
| Punkt | () | 0 | 1 | 1 | ||||||||||
| 1-Polytop | ||||||||||||||
| Strecke | {} | 1 | 1 | 2 | 1 | |||||||||
| Winkel | 1 | 1 | 3 | 2 | ||||||||||
| Punkte verbunden[12] | 1 | 1 | n | n−1 | ||||||||||
| Polygon | ||||||||||||||
| Zweieck | {2} | 2 | 1 | 2 | 2 | 1 | ||||||||
| Dreieck | {3} | 2 | 1 | 3 | 3 | 1 | ||||||||
| Viereck | {4} | 2 | 1 | 4 | 4 | 1 | ||||||||
| Fünfeck | {5} | 2 | 1 | 5 | 5 | 1 | ||||||||
| n-Eck, nicht überschlagen | {n} | 2 | 1 | n | n | 1 | ||||||||
| 2 Dreiecke mit gemeinsamer Ecke | 2 | 1 | 5 | 6 | 2 | |||||||||
| 2 Dreiecke mit gemeinsamer Kante | 2 | 1 | 4 | 5 | 2 | |||||||||
| Polyeder | ||||||||||||||
| Tetraeder | {3,3} | 3 | 1 | 4 | 6 | 4 | 1 | |||||||
| Hexaeder | {4,3} | 3 | 1 | 8 | 12 | 6 | 1 | |||||||
| Oktaeder | {3,4} | 3 | 1 | 6 | 12 | 8 | 1 | |||||||
| Dodekaeder | {5,3} | 3 | 1 | 20 | 30 | 12 | 1 | |||||||
| Ikosaeder | {3,5} | 3 | 1 | 12 | 30 | 20 | 1 | |||||||
| quadratische Doppelpyramide mit gemeinsamer Spitze | 3 | 1 | 9 | 16 | 10 | 2 | ||||||||
| Polychor | ||||||||||||||
| Pentachoron | {3,3,3} | 4 | 1 | 5 | 10 | 10 | 5 | 1 | ||||||
| 16-Zeller (Hexadekachor) | {4,3,3} | 4 | 1 | 8 | 24 | 32 | 16 | 1 | ||||||
| Tesserakt | {3,3,4} | 4 | 1 | 16 | 32 | 24 | 8 | 1 | ||||||
| 24-Zeller (Ikositetrachor) | {3,4,3} | 4 | 1 | 24 | 96 | 96 | 24 | 1 | ||||||
| 120-Zeller (Hekatonikosachor) | {5,3,3} | 4 | 1 | 600 | 1200 | 720 | 120 | 1 | ||||||
| 600-Zeller (Hexakosichor) | {3,3,5} | 4 | 1 | 120 | 720 | 1200 | 600 | 1 | ||||||
| Simplex | ||||||||||||||
| Punkt | () | 0 | 1 | 1 | ||||||||||
| Strecke | {} | 1 | 1 | 2 | 1 | |||||||||
| Dreieck | {3} | 2 | 1 | 3 | 3 | 1 | ||||||||
| Tetraeder | {3,3} | 3 | 1 | 4 | 6 | 4 | 1 | |||||||
| Pentachoron | {3,3,3} | 4 | 1 | 5 | 10 | 10 | 5 | 1 | ||||||
| 5-Simplex | {3,3,3,3} | 5 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | |||||
| 6-Simplex | {35} | 6 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | ||||
| 7-Simplex | {36} | 7 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | |||
| d-Simplex | {3d−1} | d | 1 | 1 | ||||||||||
| Hyperwürfel | ||||||||||||||
| Punkt | () | 0 | 1 | 1 | ||||||||||
| Strecke | {} | 1 | 1 | 2 | 1 | |||||||||
| Viereck | {4} | 2 | 1 | 4 | 4 | 1 | ||||||||
| Hexaeder | {4,3} | 3 | 1 | 8 | 12 | 6 | 1 | |||||||
| Tesserakt | {4,3,3} | 4 | 1 | 16 | 32 | 24 | 8 | 1 | ||||||
| 5-Kubus | {4,3,3,3} | 5 | 1 | 32 | 80 | 80 | 40 | 10 | 1 | |||||
| 6-Kubus | {4,34} | 6 | 1 | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||||
| 7-Kubus | {4,35} | 7 | 1 | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |||
| d-Kubus | {4,3d−2} | d | 1 | 1 | ||||||||||
| Kreuzpolytop | ||||||||||||||
| Strecke | {} | 1 | 1 | 2 | 1 | |||||||||
| Viereck | {4} | 2 | 1 | 4 | 4 | 1 | ||||||||
| Oktaeder | {3,4} | 3 | 1 | 6 | 12 | 8 | 1 | |||||||
| 16-Zeller (Hexadekachor) | {3,3,4} | 4 | 1 | 8 | 24 | 32 | 16 | 1 | ||||||
| 5-Orthoplex | {3,3,3,4} | 5 | 1 | 10 | 40 | 80 | 80 | 32 | 1 | |||||
| 6-Orthoplex | {34,4} | 6 | 1 | 12 | 60 | 160 | 240 | 192 | 64 | 1 | ||||
| 7-Orthoplex | {35,4} | 7 | 1 | 14 | 84 | 280 | 560 | 672 | 448 | 128 | 1 | |||
| d-Orthoplex | {3d−2,4} | d | 1 | 1 | ||||||||||
Literatur
- David Richeson: The polyhedral formula. In: Robert Bradley, Edward Sandifer (Hrsg.): Euler: Life, Work, Legacy. Elsevier, 2007.
- David Richeson: Euler’s gem. Princeton University Press, 2008.
Weblinks
- 20 verschiedene Beweise auf Englisch, unter anderem der oben angegebene ungewöhnliche Beweis mit Hilfe des Satzes von Pick.
- Eric W. Weisstein: Polyhedral Formula. In: MathWorld (englisch).
- Abigail Kirk: Euler’s Polyhedron Formula. Plus Magazine, 2007.
Einzelnachweise
- ↑ Wenn das Polyeder elastisch wäre und man in sein Inneres eine große Kugel bringen könnte, könnte man es auf dieser Kugel aufspannen.
- ↑ Darauf wies zuerst Louis Poinsot 1810 hin.
- ↑ The Euler Archive. In: scholarlycommons.pacific.edu. Abgerufen am 1. August 2021.
- ↑ Euler: Elementa doctrine solidorum. In: Novi comm. acad. scientiarum imperialis petropolitanae. 4, 1758, S. 72–93 (Eneström-Index E 230). Euler: Demonstratio nonnullarum insignium proprietatum quibus solida hedris planis inclusa sunt praedita. In: Novi Commentarii Academiae Scientiarum Petropolitanae. 4, 1758, S. 94–108 (sein Beweis, E 231). Nachdruck in Opera Omnia. Band 26. Die beiden Arbeiten stammen schon von 1750 bzw. 1751.
- ↑ E. de Jonquières: Note sur une pointe fundamental de la théorie des polyèdres. In: Comptes Rendus Acad. Sci. Paris, 110, 1890, S. 110–115. Aus Descartes’ nachgelassenen Schriften, überliefert nur aus einer Kopie von Gottfried Wilhelm Leibniz, 1860 in der Landesbibliothek Hannover entdeckt. Richeson: The polyhedral formula. Siehe Literatur.
- ↑ Dargestellt in David Richeson: Eulers gem. Princeton University Press 2008, Kapitel 7, S. 67 ff.
- ↑ Cauchy: Recherches sur les polyèdres. In: J. Ecole Polytechnique. 9, 1813, S. 68–98.
- ↑ David Richeson: Eulers gem. Princeton University Press, 2008, Kapitel 12.
- ↑ Zum Beispiel: Aigner, Ziegler: Proofs from the Book. Springer Verlag, 2010, Kapitel 12 Three applications of Euler’s Formula. David Richeson: The polyhedral formula. In: Bradley, Sandifer: Euler. Elsevier, 2007, S. 434. Er wird auch in H. S. M. Coxeter: Regular Polytopes dargestellt. Hier in der Graphentheorie-Version von Aigner, Ziegler.
- ↑ Historisch leitete Staudt damit ein Kriterium für die Polyeder ab, für die der Satz zutrifft.
- ↑ D. DeTemple, J. M. Robertson: The equivalence of Euler’s and Pick’s theorems. In: American Mathematical Monthly. Band 98, 1991, S. 97–108.
- ↑ …, sodass gerade ein geschlossener Graph entsteht; außerdem ohne „Überschlag“, d. h., die Verbindungslinien kreuzen sich nicht.
Auf dieser Seite verwendete Medien
Cyan check mark (✓) icon on a transparent background. Slight gradient between "Green30" (#14866D) and "Green50" (#00AF89)
Autor/Urheber: , Lizenz: PD-Schöpfungshöhe
Ein erläuternde Animation zu einem Beweis von Eulers Polyedersatz
Szilassi多面體的旋轉動畫
Simple picture of a Stella octangula / Star Tetrahedron
Vierkant-Viereck-Torus
Autor/Urheber: Klaus-Dieter Keller, Lizenz: CC0
Ecke, Kante und Fläche eines Würfels
Autor/Urheber: Tomruen, Lizenz: CC BY-SA 4.0
en:tetrahemihexahedron
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
A dual face coloring of the octahedral graph
Red "X"/Cross logic icon.
(c) Wrzlprmft, CC BY-SA 3.0
Ein erläuterndes Bild zu Eulers Polyedersatz: Ein planarer Graph, dem kein Polyeder zugrunde liegt.