Epigraph (Mathematik)

In der Mathematik bezeichnet der Epigraph einer reellwertigen Funktion ${\displaystyle f\colon X\to \mathbb {R} }$ die Menge aller Punkte, die auf oder über ihrem Graphen liegen.

${\displaystyle \operatorname {epi} f:=\left\{(x,\mu )\in X\times \mathbb {R} \,:\,f(x)\leq \mu \right\}\subseteq X\times \mathbb {R} }$

Ist der Bildraum der Funktion der ${\displaystyle \mathbb {R} ^{n}}$ versehen mit einer verallgemeinerten Ungleichung ${\displaystyle \preccurlyeq _{K}}$, so ist der Epigraph definiert als

${\displaystyle \operatorname {epi} f:=\left\{(x,\mu )\in X\times \mathbb {R} ^{n}\,:\,f(x)\preccurlyeq _{K}\mu \right\}\subseteq X\times \mathbb {R} ^{n}}$.

Eigenschaften

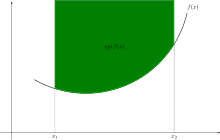
Sei ${\displaystyle X}$ ein normierter ${\displaystyle \mathbb {R} }$-Vektorraum. Für Funktionen ${\displaystyle f\colon X\rightarrow \mathbb {R} }$ gilt:

• ${\displaystyle f}$ ist genau dann konvex, wenn der Epigraph von ${\displaystyle f}$ eine konvexe Menge bildet.
• ${\displaystyle f}$ ist genau dann halbstetig von unten, wenn der Epigraph von ${\displaystyle f}$ eine abgeschlossene Menge bildet.
• ${\displaystyle f}$ ist genau dann schwach unterhalbstetig, wenn der Epigraph von ${\displaystyle f}$ eine schwach folgenabgeschlossene Menge ist.
• Ist ${\displaystyle f}$ eine affin-lineare Funktion, dann definiert ihr Epigraph einen Halbraum in ${\displaystyle X}$.

Ist der Bildraum der Funktion der ${\displaystyle \mathbb {R} ^{n}}$, so ist sie genau dann K-konvex, wenn der Epigraph konvex ist.

Siehe auch

• Hypograph

Literatur

• Johannes Jahn: Introduction to the Theory of Nonlinear Optimization. 3. Auflage. Springer-Verlag, Berlin Heidelberg New York 2007, ISBN 978-3-540-49378-5. 
• Ralph Tyrell Rockafellar: Convex Analysis. Princeton University Press, Princeton 1997, ISBN 0-691-01586-4

Weblinks

Commons: Epi- und Hypographen – Sammlung von Bildern, Videos und Audiodateien