Enneper-Weierstraß-Konstruktion

Die Weierstraß-Darstellung, manchmal auch Enneper-Weierstraß- oder Weierstraß-Enneper-Konstruktion, ist eine nach Karl Weierstraß bzw. Alfred Enneper benannte Darstellung von Minimalflächen. Letztere sind reguläre Flächen im reellen Vektorraum ${\displaystyle \mathbb {R} ^{3}}$, die in der Natur als Seifenhautflächen vorkommen, und daher "reelle" Gebilde. Es mag daher verwundern, dass bei deren Beschreibung holomorphe Funktionen zu Tage treten, wie das bei der hier zu besprechenden Darstellung der Fall ist.

Enneper-Weierstraß-Darstellung

Es seien ${\displaystyle U\subset \mathbb {C} }$ eine einfach zusammenhängende Menge,

${\displaystyle z_{0}\in U}$,   ${\displaystyle c_{1},c_{2},c_{3}\in \mathbb {R} }$,

${\displaystyle F:U\rightarrow \mathbb {C} }$ eine von der Nullfunktion verschiedene holomorphe Funktion

${\displaystyle G:U\rightarrow {\hat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}}$ eine meromorphe Funktion,

so dass das Produkt ${\displaystyle FG^{2}}$ holomorph ist, das heißt an allen Polstellen von ${\displaystyle G}$ eine hebbare Definitionslücke hat. Setze

${\displaystyle \varphi _{1}(\zeta ):={\frac {1}{2}}F(\zeta )(1-G^{2}(\zeta ))}$,

${\displaystyle \varphi _{2}(\zeta ):={\frac {\mathrm {i} }{2}}F(\zeta )(1+G^{2}(\zeta ))}$,

${\displaystyle \varphi _{3}(\zeta ):=F(\zeta )G(\zeta )}$,

Dann ist durch

${\displaystyle f_{j}(x,y)=c_{j}+\operatorname {Re} \int _{z_{0}}^{x+\mathrm {i} y}\varphi _{j}(\zeta )\mathrm {d} \zeta \quad \quad j=1,2,3}$

eine Parametrierung

${\displaystyle f=(f_{1},f_{2},f_{3}):U\rightarrow \mathbb {R} ^{3}}$ einer Minimalfläche gegeben.

Umgekehrt kann jede Minimalfläche lokal auf diese Weise parametrisiert werden, das heißt, man kann Daten ${\displaystyle U,z_{0},c_{1},c_{2},c_{3},F,G}$ wie oben finden, so dass die dadurch definierten ${\displaystyle f_{1},f_{2},f_{3}}$ die vorgelegte Minimalfläche in einer Umgebung von ${\displaystyle (c_{1},c_{2},c_{3})}$ parametrisieren.^[1][2][3]

Dabei bedeutet ${\displaystyle \operatorname {Re} }$ die Realteilbildung, das Integral von ${\displaystyle z_{0}}$ nach ${\displaystyle x+\mathrm {i} y}$ ist längs irgendeines Integrationsweges in ${\displaystyle U}$ zu bilden, wegen des vorausgesetzten einfachen Zusammenhangs hängt der Wert des Integrals nicht vom gewählten Integrationsweg ab.

Ergänzungen

Obige Darstellung stammt von Karl Weierstraß aus dem Jahre 1866, etwa zeitgleich wurden gleichwertige Formeln von Alfred Enneper und Bernhard Riemann verwendet.^[4]

In obigem Satz liefert die Umkehrung die Existenz einer gewissen Parametrisierung einer Minimalfläche. Oft sind Flächen aber schon in Form einer Parametrisierung gegeben, so dass sich die Frage stellt, ob die Funktionen ${\displaystyle F}$ und ${\displaystyle G}$ auch zu einer vorgegebenen Parametrisierung einer Minimalfläche gefunden werden können. Das ist im Allgemeinen nicht der Fall, wohl aber, wenn die vorgegebene Parametrisierung konform ist, das heißt, wenn die erste Fundamentalform ein Vielfaches der Einheitsmatrix ist, genauer, wenn ${\displaystyle (g_{ij})=\lambda \cdot {\begin{pmatrix}1&0\\0&1\end{pmatrix}}}$ für eine skalare Funktion ${\displaystyle \lambda }$, wobei ${\displaystyle (g_{ij})}$ den Metriktensor bezeichnet. Das wird in der unten angegebenen Beweisskizze deutlich.

Das Paar ${\displaystyle (F,G)}$ heißt eine Weierstraß-Darstellung der Minimalfläche. Dabei lässt man oft die Konstanten ${\displaystyle c_{1},c_{2},c_{3}\in \mathbb {R} }$ außer Acht, das heißt man verschiebt die Fläche in Gedanken so, dass der Nullpunkt innerhalb der Fläche liegt. Die holomporhen Funktionen ${\displaystyle \varphi _{j}}$ erfüllen

${\displaystyle \varphi _{1}^{2}+\varphi _{2}^{2}+\varphi _{3}^{2}={\frac {1}{4}}F^{2}(1-G^{2})^{2}-{\frac {1}{4}}F^{2}(1+G^{2})^{2}+F^{2}G^{2}=0}$.

Hat man umgekehrt drei nicht identisch verschwindende, holomorphe Funktionen ${\displaystyle \varphi _{1},\varphi _{2},\varphi _{3}:U\rightarrow \mathbb {C} }$ mit ${\displaystyle \varphi _{1}^{2}+\varphi _{2}^{2}+\varphi _{3}^{2}=0}$ gegeben, so kann man eine holomorphe Funktion ${\displaystyle F}$ und eine meromorphe Funktion ${\displaystyle G}$ wie im Satz finden, leicht überlegt man sich, dass

${\displaystyle F:=\varphi _{1}-\mathrm {i} \varphi _{2}}$   und   ${\displaystyle G:={\frac {\varphi _{3}}{\varphi _{1}-\mathrm {i} \varphi _{2}}}}$

das Verlangte leisten.

Wenn ${\displaystyle G}$ konstant ist, dann sind ${\displaystyle \varphi _{1}}$ und ${\displaystyle \varphi _{3}}$ offenbar proportional und man erhält die Parametrisierung einer Ebene. Viele Autoren schließen diesen trivialen Fall aus und das wollen wir hier auch tun.

Beispiel

Man kann gemäß der Weierstraß-Darstellung zu vorgegebenen Funktionen ${\displaystyle F}$ und ${\displaystyle G}$, die die genannten Bedingungen erfüllen, Minimalflächen konstruieren. Ein sehr einfacher und bekannter Fall ist die Enneperfläche, die man aus ${\displaystyle F(\zeta )=2}$ (konstante Funktion) und ${\displaystyle G(\zeta )=\zeta }$ auf ${\displaystyle U=\mathbb {C} }$ erhält. Die Funktionen ${\displaystyle \varphi _{j}}$ ergeben sich nach obigen Formeln zu

${\displaystyle \varphi _{1}(\zeta )=1-\zeta ^{2}}$

${\displaystyle \varphi _{2}(\zeta )=\mathrm {i} (1+\zeta ^{2})}$

${\displaystyle \varphi _{3}(\zeta )=2\zeta }$.

Es handelt sich also durchweg um Polynome, deren Integration trivial ist. Als ${\displaystyle z_{0}}$ wählen wir den Nullpunkt, auch die Konstanten ${\displaystyle c_{i}}$ setzen wir zu 0 an. Dann erhält man für ${\displaystyle z=x+\mathrm {i} y}$

${\displaystyle {\begin{aligned}f_{1}(z)&=\operatorname {Re} \int _{0}^{z}(1-\zeta ^{2})\mathrm {d} \zeta =\operatorname {Re} (\zeta -{\frac {1}{3}}\zeta ^{3})|_{0}^{z}\\&=\operatorname {Re} (z-{\frac {1}{3}}z^{3})=\operatorname {Re} (x+\mathrm {i} y-{\frac {1}{3}}(x^{3}+3\mathrm {i} x^{2}y+3\mathrm {i} ^{2}xy^{2}+\mathrm {i} ^{3}y^{3}))=x-{\frac {1}{3}}x^{3}+xy^{2}\end{aligned}}}$

und durch ähnliche einfache Rechnungen

${\displaystyle f_{2}(z)=-y+{\frac {1}{3}}y^{3}-x^{2}y}$

${\displaystyle f_{3}(z)=x^{2}-y^{2}}$

Daher ist durch

${\displaystyle f(x,y):=(x-{\frac {1}{3}}x^{3}+xy^{2},-y+{\frac {1}{3}}y^{3}-x^{2}y,x^{2}-y^{2})}$

die Parametrisierung einer Minimalfläche gegeben, diese nennt man nach ihrem Entdecker die Enneperfläche.

Beweisskizze

Die folgende Beweisskizze enthält wenig von den erforderlichen technischen Details. Die einfachere Richtung geht von den Funktionen ${\displaystyle F}$ und ${\displaystyle G}$ aus und konstruiert die im Satz angegebene konforme Parametrisierung ${\displaystyle f_{1},f_{2},f_{3}}$. Dieses Vorgehen wurde auch am Beispiel der Enneperfläche verdeutlicht. Unter Ausnutzung der Analytizität zeigt man schließlich, dass die mittlere Krümmung der dadurch definierten Fläche verschwindet und daher eine Minimalfläche vorliegt.

Ist umgekehrt eine Minimalfläche in parametrisierter Form gegeben, so erfolgt die Ermittlung der Enneper-Weierstraß-Darstellung in folgenden Schritten, die im Wesentlichen eine Umkehrung der obigen Konstruktion darstellen, wobei eine zusätzliche Schwierigkeit darin besteht, dass man sich zunächst eine konforme Parametrisierung verschaffen muss.

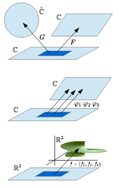
Krümmungslinienparameter

Als erstes ermittelt man die sogenannten Krümmungslinienparameter. Das ist eine Parametrisierung, ${\displaystyle f:U\rightarrow \mathbb {R} ^{3}}$, so dass die erste und zweite Fundamentalform Diagonalgestalt haben. Für ein Flächenstück ohne Nabelpunkte ist das lokal durch Lösen einer partiellen Differentialgleichung stets möglich.^[5] Es gilt dann ${\displaystyle \textstyle {\frac {\partial \nu }{\partial u_{i}}}=-\kappa _{i}{\frac {\partial f}{\partial u_{i}}}}$, wobei ${\displaystyle \nu }$ das Normalenfeld und die ${\displaystyle \kappa _{i}}$ die beiden Hauptkrümmungen sind. Da bei einer Minimalfläche die mittlere Krümmung ${\displaystyle \textstyle {\frac {1}{2}}(\kappa _{1}+\kappa _{2})}$ verschwindet, muss ${\displaystyle \kappa :=\kappa _{1}=-\kappa _{2}}$ sein.

Konforme Parameter

Im zweiten Schritt konstruieren wir konforme Parameter, siehe oben. Wir geben uns einen Punkt ${\displaystyle (x_{0},y_{0})\in U}$ vor und gehen zu einer in ${\displaystyle U}$ enthaltenen Rechteckumgebung ${\displaystyle U_{0}}$ über. Das kann man tun, da es sich ja um ein lokales Problem handelt. Bezeichnet wieder ${\displaystyle (g_{ij})}$ die Metrik aus der ersten Fundamentalform, so überlegt man sich, dass die Funktionen ${\displaystyle \kappa \cdot g_{ii}:U\rightarrow \mathbb {R} ^{3}}$, die ja von Paaren ${\displaystyle (x,y)\in U_{0}}$ abhängen, tatsächlich nur von einer der Variablen abhängen, indem man zeigt, dass die Ableitung nach der jeweils anderen Variablen verschwindet. Es gibt daher reelle Funktionen ${\displaystyle \Phi _{1},\Phi _{2}}$ mit ${\displaystyle \Phi _{1}(x)=\kappa (x,y)\cdot g_{11}(x,y)}$ und ${\displaystyle \Phi _{2}(y)=\kappa (x,y)\cdot g_{22}(x,y)}$. Die Funktionen ${\displaystyle \Phi _{j}}$ sind positiv und man kann damit folgende Abbildung definieren:

${\displaystyle \Phi :U_{0}\rightarrow \mathbb {R} ^{2},\quad \Phi (x,y):={\begin{pmatrix}v_{1}(x)\\v_{2}(y)\end{pmatrix}}}$, wobei

${\displaystyle v_{1}(x):=\int _{x_{1}}^{x}{\sqrt {\Phi _{1}(x)}}\mathrm {d} x,\quad v_{2}(y):=\int _{y_{1}}^{y}{\sqrt {\Phi _{2}(y)}}\mathrm {d} y}$.

Dann ist ${\displaystyle \Phi }$ ein Diffeomorphismus von ${\displaystyle U_{0}}$ auf das Bild ${\displaystyle V:=\Phi (U_{0})}$ und man zeigt, dass die drei Funktionen

${\displaystyle f_{j}\circ \Phi ^{-1}:V\rightarrow \mathbb {R} ,\quad j=1,2,3}$

eine konforme Parametrisierung des vorgelegten Flächenstücks bilden.^[6]

Holomorphe Funktionen

An dieser Stelle der Konstruktion liegt also eine konforme Parametrisierung ${\displaystyle f_{j}:U\rightarrow \mathbb {R} }$ vor und ${\displaystyle U}$ kann der Einfachheit halber als offenes Rechteck in der Ebene angenommen werden. Identifiziert man die Ebene wie üblich mit der Ebene ${\displaystyle \mathbb {C} }$ der komplexen Zahlen, so erhalten wir drei komplexe Funktionen ${\displaystyle \varphi :U\rightarrow \mathbb {C} }$ durch

${\displaystyle \varphi _{1}(x+\mathrm {i} y):={\frac {\partial f_{1}}{\partial x}}(x,y)-\mathrm {i} \cdot {\frac {\partial f_{1}}{\partial y}}(x,y)}$

${\displaystyle \varphi _{2}(x+\mathrm {i} y):={\frac {\partial f_{2}}{\partial x}}(x,y)-\mathrm {i} \cdot {\frac {\partial f_{2}}{\partial y}}(x,y)}$

${\displaystyle \varphi _{3}(x+\mathrm {i} y):={\frac {\partial f_{3}}{\partial x}}(x,y)-\mathrm {i} \cdot {\frac {\partial f_{3}}{\partial y}}(x,y)}$

Die Konformität der Parametrisierung ist äquivalent zu ${\displaystyle \varphi _{1}^{2}+\varphi _{2}^{2}+\varphi _{3}^{2}=0}$ und die Minimalflächeneigenschaft ist in dieser Situation äquivalent zur Holomorphie der ${\displaystyle \varphi _{j}}$.^[7] Mit den bereits oben genannten Formeln

${\displaystyle F:=\varphi _{1}-\mathrm {i} \varphi _{2}}$   und   ${\displaystyle G:={\frac {\varphi _{3}}{\varphi _{1}-\mathrm {i} \varphi _{2}}}}$

erhält man die gewünschte Weierstraß-Darstellung.^[8]

Einzelnachweise

1. ↑ Wolfgang Kühnel: Differentialgeometrie, ISBN 978-3-8348-0411-2, Folgerung 3.36: Weierstraß-Darstellung
2. ↑ Jost-Hinrich Eschenburg, Jürgen Jost: Differentialgeometrie und Minimalflächen, Springer-Verlag 2014, ISBN 978-3-642-38521-6, Kapitel 8.5: Die Weierstraß-Darstellung
3. ↑ Johannes Nitsche: Vorlesungen über Minimalflächen, Springer-Verlag (1975), ISBN 978-3-642-65620-0, Kapitel III.2.3: Die Weierstraß-Enneperschen Darstellungsformeln
4. ↑ Johannes Nitsche: Vorlesungen über Minimalflächen, Springer-Verlag (1975), ISBN 978-3-642-65620-0, historische Bemerkung auf Seite 143
5. ↑ Wilhelm Blaschke, Kurt Leichtweiß: Elementare Differentialgeometrie, Springer-Verlag 1973, ISBN 0-3870-5889-3, §46: Krümmungslinien
6. ↑ Wolfgang Kühnel: Differentialgeometrie, ISBN 978-3-8348-0411-2, Lemma 3.33
7. ↑ Wolfgang Kühnel: Differentialgeometrie, ISBN 978-3-8348-0411-2, Folgerung 3.31
8. ↑ Wolfgang Kühnel: Differentialgeometrie, ISBN 978-3-8348-0411-2, Lemma 3.35