Einmaleins

Das kleine Einmaleins (auch 1×1 oder 1mal1) ist eine Zusammenstellung aller Produkte, die sich aus der Kombination zweier natürlicher Zahlen von 1 bis 10 ergeben, meist in Tabellenform. Das große Einmaleins ist die Erweiterung auf natürliche Zahlen von 1 bis 20. Das kleine Einmaleins gehört zum arithmetischen Grundwissen der Mathematik und wird meist in der Grundschule auswendig gelernt.
Als Einmaleins werden metaphorisch auch Grundkenntnisse eines Wissensgebiets oder einer Fertigkeit bezeichnet.
Anwendung
Das kleine Einmaleins wird beim schriftlichen Multiplizieren zum Auffinden des Produkts der einzelnen Ziffern beider Faktoren verwendet. Hierfür werden nur die Produkte aus den Ziffernkombinationen bis benötigt, wobei die Produkte mit einem Faktor 0 in der Darstellung meist weggelassen werden, dafür werden aus der Tradition der Verwendung römischer Ziffern die Produkte mit einem Faktor 10 ergänzt.[1][2]
“But, to shorten the repeated summation of digits, it is expedient to construct a table, which must be engraved in the memory of the arithmetician.”
„Um aber das wiederholte Addieren von Ziffern zu verkürzen, ist es nützlich, eine Tabelle anzufertigen, die ins Gedächtnis des Arithmetikers eingeprägt werden muss.“
Dies wird auch bei der schriftlichen Division genutzt.
Das große Einmaleins dient zum Auswendiglernen oft benötigter Produkte.
Darstellung
Nach Adam Ries
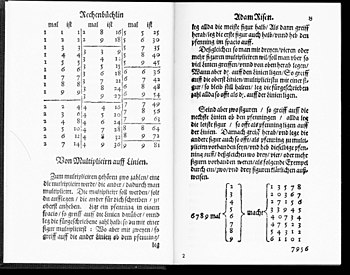
In Adam Risen Rechenbuch von 1574 ist folgende Einmaleins-Tabelle dargestellt mit dem Hinweis „du mußt vor allen Dingen das Einmal eins wol wissen und auswendig lernen wie hie:“ (Adam Ries)[4]
| mal | ist | mal | ist | mal | ist | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 8 | 16 | 5 | 5 | 25 | ||
| 1 | 2 | 2 | 2 | 9 | 18 | 5 | 6 | 30 | ||
| 1 | 3 | 3 | 3 | 3 | 9 | 5 | 7 | 35 | ||
| 1 | 4 | 4 | 3 | 4 | 12 | 5 | 8 | 40 | ||
| 1 | 5 | 5 | 3 | 5 | 15 | 5 | 9 | 45 | ||
| 1 | 6 | 6 | 3 | 6 | 18 | 6 | 6 | 36 | ||
| 1 | 7 | 7 | 3 | 7 | 21 | 6 | 7 | 42 | ||
| 1 | 8 | 8 | 3 | 8 | 24 | 6 | 8 | 48 | ||
| 1 | 9 | 9 | 3 | 9 | 27 | 6 | 9 | 54 | ||
| 2 | 2 | 4 | 4 | 4 | 16 | 7 | 7 | 49 | ||
| 2 | 3 | 6 | 4 | 5 | 20 | 7 | 8 | 56 | ||
| 2 | 4 | 8 | 4 | 6 | 24 | 7 | 9 | 63 | ||
| 2 | 5 | 10 | 4 | 7 | 28 | 8 | 8 | 64 | ||
| 2 | 6 | 12 | 4 | 8 | 32 | 8 | 9 | 72 | ||
| 2 | 7 | 14 | 4 | 9 | 36 | 9 | 9 | 81 |
Diese kompakte Darstellung verzichtet auf redundante Informationen unter Ausnutzung des Kommutativgesetzes (2 · 3 = 3 · 2). Sie diente als Hilfsmittel beim Rechnen auf Linien.
Tabelle
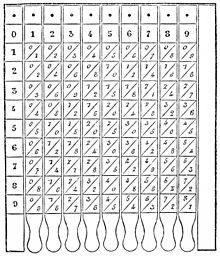
Die ausführliche tabellarische Darstellung des kleinen Einmaleins wird Pythagoras zugeschrieben und daher in manchen Sprachen auch Pythagorasbrett bzw. Pythagorastabelle genannt, zum Beispiel im Französischen, Englischen und Italienischen, aber auch in der Montessoripädagogik.[6][3][7]
Die folgende Tabelle stellt das kleine Einmaleins dar.
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Unterteilt wird das Einmaleins entsprechend dem zweiten Faktor in die 1er-Reihe, 2er-Reihe, 3er-Reihe usw. bis zur 10er-Reihe. Eine Tabellenspalte stellt also die entsprechende Reihe dar. In der ersten Spalte (links) wird der erste Faktor, in der ersten Zeile (oben) wird der zweite Faktor gesucht, im Schnittpunkt der Zeile mit der Spalte steht das Produkt.
Die folgende Tabelle stellt das große Einmaleins mit Faktoren bis 20 dar (einschließlich des kleinen Einmaleins).
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Reihen
Einzeln werden die Reihen des kleinen Einmaleins wie folgt dargestellt:
1er-Reihe | 2er-Reihe | 3er-Reihe | 4er-Reihe | 5er-Reihe |
6er-Reihe | 7er-Reihe | 8er-Reihe | 9er-Reihe | 10er-Reihe |
Vergleichbares in anderen Zahlensystemen und Zahlschriften
Ein Einmaleins ist aus der Zeit um Christi Geburt in Griechischer Zahlschrift überliefert. Die Aufzeichnung eines Schülers gilt als Beleg, dass zu der Zeit das Einmaleins gelehrt und gelernt wurde.[8]
493 stellte Victorius von Aquitanien zur Erleichterung der Multiplikation und Division ein Tafelwerk mit 98 Spalten zusammen, in denen er die Produkte der Zahlen von den Brüchen bis zum Wert 1000 mit den Zahlen von 2 bis 50 in Römischer Zahlschrift angab, der sogenannte Calculus Victorii.[9]
Für das Sexagesimalsystem wurde von Gaspar Schott die Tabula Sexagenaria 1661 veröffentlicht.[10]
Siehe auch
- Das Hexeneinmaleins aus Johann Wolfgang von Goethes Faust. Eine Tragödie
- Das Titellied Hey, Pippi Langstrumpf der Fernsehserie Pippi Langstrumpf.
Weblinks
Einzelnachweise
- ↑ Stephan Weiss: The Small Multiplication Table through the Centuries in Europe. (PDF; 2,0 MB) In: Journal of the Oughtred Society, 22, Fall 2013, S. 2.
- ↑ Stephan Weiss: Das Einmaleins durch die Jahrhunderte. (PDF; 2,2 MB) 2015.
- ↑ a b John Leslie: The Philosophy of Arithmetic. Edinburgh 1820, S. 148 (Textarchiv – Internet Archive).
- ↑ Adam Risen Rechenbuch auff Linien und Ziphren in allerley Hanthierung / Geschäfften unnd Kauffmanschafft. Mit neuwen künstlichen Regeln und Exempeln gemehret. 1574
- ↑ aus M. Edouard Lucas: Calculating-Machines. In: E. L. Youmans, W. J. Youmans (Hrsg.): Popular Science Monthly. Band 26. New York 1885, S. 451 (englisch, Wikisource).
- ↑ John Farrar: An Elementary Treatise on Arithmetic. Cambridge 1825, S. 17 (Textarchiv – Internet Archive).
- ↑ Maria Montessori: Entwicklungsmaterialien in der Schule des Kindes. Götz, Dörfles 2003, ISBN 3-9501011-7-9 (italienisch: L’autoeducazione nelle scuole elementari. Übersetzt von Karin Pellegrini).
- ↑ Stephan Weiss: Die Multipliziertafel, ihre Ausgestaltung und Verwendung. (PDF; 11 MB) 2003
- ↑ David W. Maher, John F. Makowski: Literary Evidence for Roman Arithmetic with Fractions. In: The University of Chicago (Hrsg.): Classical Philology. Nr. 96, 2001, S. 376–399 (englisch, dmaher.org [PDF; 1,2 MB; abgerufen am 8. Januar 2013]).
- ↑ Stephan Weiss: Reconstruction and Background of Gaspar Schott’s Tabula Sexagenaria (1661). (PDF; 5,8 MB)
Auf dieser Seite verwendete Medien
Table of Pythagoras on slats
Dies ist ein Scan des historischen Buches
Autor/Urheber: Paebi, Lizenz: CC BY-SA 4.0
Rechenbrett für Multiplikation: kleines Einmaleins


