Ebener Graph

Ein ebener Graph ist eine konkrete Darstellung eines Graphen als Teilmenge des ${\displaystyle \mathbb {R} ^{2}}$ und damit ein Spezialfall eines euklidischen Graphen für ${\displaystyle q=2}$.

Definition

Ein Tupel ${\displaystyle (V,E)}$ (wobei die Elemente aus ${\displaystyle V}$ Ecken genannt werden und die Elemente aus ${\displaystyle E}$ Kanten) heißt ein ebener Graph, wenn gilt:

• ${\displaystyle V}$ besteht aus paarweise disjunkten Punkten des ${\displaystyle \mathbb {R} ^{2}}$.
• Jede Kante ist eine einfache Jordankurve, die zwei Ecken miteinander verbindet.
• Die Kanten schneiden sich nie und berühren sich bloß in den Ecken.

Teilweise wird in der Literatur auch noch folgende vierte Bedingung gestellt:

• Verschiedene Ecken werden durch verschiedene Kanten verbunden.

Diese Verschärfung wird oftmals gefordert, wenn man nur einfache Graphen auf Planarität untersuchen will. Die obigen drei Punkte lassen noch Multigraphen als betrachteten Gegenstand zu.

Ein ebener Graph heißt maximal eben, wenn er eben ist, aber nach dem hinzufügen einer beliebigen Kante nicht mehr eben ist.

Abgrenzung zu planaren Graphen

Beispielgraphen G1 und G2

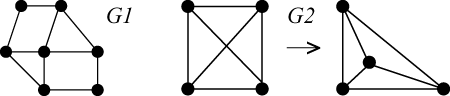
Bei ebenen Graphen besteht oftmals eine Verwechslungsgefahr zu den planaren Graphen: Planarität ist eine Eigenschaft von abstrakten Graphen, also Graphen, aufgefasst als eine Knotenmenge und je nach Definition unterschiedliche Kantenmenge. Ein ebener Graph jedoch ist eine Darstellung eines abstrakten Graphen als Teilmenge des ${\displaystyle \mathbb {R} ^{2}}$. So ist im obigen Bild ${\displaystyle G_{1}}$ eben. Betrachtet man ${\displaystyle G_{2}}$ als Teilmenge des ${\displaystyle \mathbb {R} ^{2}}$, so muss dieser erst anders gezeichnet werden, um einen ebenen Graphen zu erhalten. Der zugrunde liegende abstrakte Graph ${\displaystyle G_{2}}$ ist aber planar unabhängig davon, wie man ihn im konkreten Fall zeichnet. Definitionsgemäß sind die planaren Graphen genau diejenigen Graphen, die zu einem ebenen Graphen isomorph sind.

Eigenschaften

• Für zusammenhängende ebene Graphen gilt nach dem eulerschen Polyedersatz:

${\displaystyle n-m+f=2}$, wobei ${\displaystyle n=|V|}$, ${\displaystyle m=|E|}$ und ${\displaystyle f}$ die Anzahl der Flächen des Graphen ist (die äußere Fläche mitgerechnet)

• Jeder maximal ebene Graph ist maximal planar

Literatur

• Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (354 S., Online-Version). 
• Lutz Volkmann: Fundamente der Graphentheorie, Springer (Wien) 1996, ISBN 3-211-82774-9 (neuere, Online-Version "Graphen an allen Ecken und Kanten"; PDF; 3,7 MB)