Schnittpunkt (Darstellende Geometrie)

Schnittpunkte treten in der Darstellenden Geometrie auf als gemeinsame Punkte

• von Kurven (Geraden, Kreise, ...) in der Zeichenebene (Grundriss-, Aufrisstafel, ...).
• von Geraden im Anschauungsraum.
• von Geraden mit Ebenen, Kugel, Kegel, Zylinder, ... (im Anschauungsraum).

Wenn Geraden beteiligt sind, was meistens der Fall ist, werden die Schnittpunkte Durchstoßpunkte genannt.

Gemeinsame Punkte von Kurven und Flächen werden in der Darstellenden Geometrie nicht berechnet, sondern zeichnerisch in einer Zweitafelprojektion (Grund- und Aufriss) bestimmt und dann gegebenenfalls in eine anschaulichere Projektion (Axonometrie) übertragen.

Schnittpunkte (Durchstoßpunkte) und Schnittkurven (Durchdringungskurven) werden in Büchern über Darstellende Geometrie meist in einem gemeinsamen Kapitel Durchdringungen behandelt.

Zwei in Grund- und Aufriss gegebene Geraden im Raum haben genau dann einen

• Schnittpunkt, wenn in einer geeigneten Zweitafelprojektion sich ihre Grund- und Aufrisse schneiden und die Schnittpunkte auf demselben Ordner (Lotgerade zur Risskante) liegen (siehe Bild).

Zwei Geraden sind windschief, falls

• sich die Grundrissgeraden und die Aufrissgeraden schneiden und deren Schnittpunkte auf zwei verschiedenen Ordnern liegen oder
• die Aufrissgeraden verschieden und parallel sind und die Grundrissgeraden sich schneiden oder
• die Grundrissgeraden verschieden und parallel sind und die Aufrissgeraden sich schneiden.

Sichtbarkeitsbetrachtungen:
Bei Sichtbarkeitsbetrachtungen (s. Gerade und Dreieck, unten) ist es wichtig für zwei windschiefe Geraden zu entscheiden, welche Gerade über bzw. vor der anderen verläuft. Hierzu betrachtet man den Schnittpunkt der Grundrisse und erkennt anschließend am zu gehörigen Ordner im Aufriss, welche Gerade an dieser Stelle über der anderen verläuft (siehe Bild mit windschiefen Geraden, ${\displaystyle g_{1}}$ verläuft an der Stelle ${\displaystyle S'}$ über ${\displaystyle g_{2}}$). Analog geht man vor, um zu entscheiden, welche Gerade bei ${\displaystyle T'}$ vor der anderen verläuft.

Sind sowohl die Aufrisse als auch die Grundrisse der Geraden parallel, so sind die Geraden selbst parallel.

Bemerkung:

1. Liegen die beiden Geraden in einer Ebene ${\displaystyle \pi }$, die zur Grundrisstafel aber nicht zur Aufrisstafel senkrecht ist, so fallen die Grundrisse der Geraden zusammen. Dies ist aber kein Problem, da der Schnittpunkt im Aufriss konstruiert und anschließend in den Grundriss übertragen werden kann. Entsprechendes gilt, falls die Ebene ${\displaystyle \pi }$ nur zur Aurisstafel senkrecht ist.
2. Liegen die beiden Geraden in einer zur Risskante senkrechten Ebene ${\displaystyle \pi }$, so fallen ihre Grundrisse und Aufrisse zusammen. In diesem Fall ist die Beschreibung der Geraden durch Grund- und Aufriss nicht eindeutig und man kann keinen Schnittpunkt bestimmen. Erst durch Hinzunahme eines dritten Risses (Dreitafelprojektion) lässt sich der Schnittpunkt ermitteln.

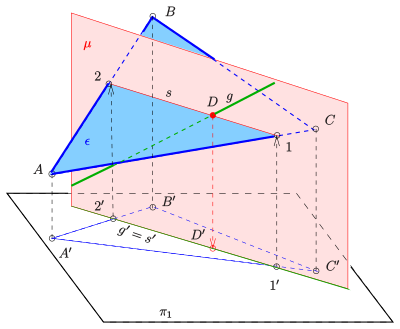
Gegeben: eine Ebene ${\displaystyle \varepsilon }$ durch ein Dreieck ${\displaystyle A,B,C}$ und eine Gerade ${\displaystyle g}$ in Grund und Aufriss.
Gesucht: der Durchstoßpunkt (Schnittpunkt) der Gerade mit der Ebene.
Zur Konstruktion verwendet man die senkrechte Hilfsebene ${\displaystyle \mu }$, die die Gerade ${\displaystyle g}$ enthält. Die Grundrisse ${\displaystyle \mu '}$ und ${\displaystyle g'}$ fallen also zusammen (s. Bild). Der Grundriss der Schnittgerade ${\displaystyle s=\varepsilon \cap \mu }$ fällt auch mit ${\displaystyle g'}$ zusammen. Damit sind die Schnittpunkte ${\displaystyle 1',2'}$ von ${\displaystyle g'}$ mit dem Dreieck die Grundrisse der Schnittpunkte ${\displaystyle 1,2}$ der Gerade ${\displaystyle s}$ mit dem Dreieck. Die Aufrisse ${\displaystyle 1'',2''}$ findet man über Ordner. Somit ist ${\displaystyle s''}$ bekannt und kann mit ${\displaystyle g''}$ geschnitten werden. ${\displaystyle D''=s''\cap g''}$ ist der Aufriss des gesuchten Durchstoßpunktes ${\displaystyle D}$. Der Grundriss ${\displaystyle D'}$ liegt auf dem zugehörigen Ordner und ${\displaystyle g'}$.

Falls es geeignet erscheint, kann man die Hilfsebene ${\displaystyle \mu }$ auch senkrecht zur Aufrisstafel wählen. Dann beginnt die Konstruktion im Aufriss.

Zur Sichtbarkeit: An der Stelle ${\displaystyle 2'}$ erkennt man, dass die Gerade ${\displaystyle g}$ über der Dreiecksseite ${\displaystyle {\overline {AB}}}$ verläuft. Die Gerade ${\displaystyle g}$ ist also im Grundriss zwischen den Punkten ${\displaystyle 2'}$ und ${\displaystyle D'}$ sichtbar und zwischen ${\displaystyle D'}$ und ${\displaystyle 1'}$ durch das Dreieck (als Fläche) verdeckt.

Die Bestimmung der Schnittpunkte einer Gerade mit einem senkrechten Kreiszylinder, der senkrecht auf der Grundrisstafel steht, ist besonders einfach: Man erhält die Grundrisse der Schnittpunkte als Schnittpunkte des Grundrisses der Gerade mit dem Grundriss des Zylinders (Kreis) und überträgt die Schnittpunkte über Ordner auf die Gerade im Aufriss (s. Bild).

Falls der Zylinder nicht senkrecht auf Grund- oder Aufrisstafel steht, führt man eine neue Risstafel so ein, dass dies in den neuen zugeordneten Rissen der Fall ist (siehe Schnittpunkt Gerade-Kugel).

Gegeben: Grund- und Aufriss einer Kugel ${\displaystyle k}$ und einer Gerade ${\displaystyle g}$.
Gesucht: die Schnittpunkte ${\displaystyle A,B}$ der Gerade mit der Kugel.
Als Hilfsebene wählt man hier die senkrechte Ebene ${\displaystyle \varepsilon }$ durch die Gerade ${\displaystyle g}$. ${\displaystyle \varepsilon }$ schneidet die Kugel in einem Kreis ${\displaystyle c}$. Die Schnittpunkte der Gerade mit dem Kreis liefert die gesuchten Schnittpunkte ${\displaystyle A,B}$.

Durchführung der Konstruktion:
Der Grundriss der Hilfsebene ${\displaystyle \varepsilon }$ fällt mit dem Grundriss ${\displaystyle g'}$ der Gerade ${\displaystyle g}$ zusammen. Um die Schnittpunkte ${\displaystyle A,B}$ bestimmen zu können, wird eine neue Rissebene ${\displaystyle \pi _{3}}$ so eingeführt, dass sie parallel zur Ebene ${\displaystyle \varepsilon }$ ist, d. h. die neue Risskante ${\displaystyle k_{13}}$ muss zu ${\displaystyle g'}$ parallel sein. Nach Wahl einer Risskante ${\displaystyle k_{13}}$ konstruiert man die neuen Risse der Kugel, des Kreises ${\displaystyle c}$ und der Gerade ${\displaystyle g}$ (siehe hierzu Zweitafelprojektion). Die Schnittpunkte der Gerade ${\displaystyle g'''}$ mit dem Kreis ${\displaystyle c'''}$ liefern zunächst die Risse ${\displaystyle A''',B'''}$ der gesuchten Punkte ${\displaystyle A,B}$. Über die zugehörigen Ordner findet man schließlich ${\displaystyle A',B'}$ und dann ${\displaystyle A'',B''}$.

Gegeben: Grund- und Aufriss eines Kegels ${\displaystyle k}$ und einer Gerade ${\displaystyle g}$.
Gesucht: die Schnittpunkte ${\displaystyle A,B}$ der Gerade mit dem Kegel.
In diesem Fall benutzt man keine senkrechte Hilfsebene, sondern die schräge Ebene ${\displaystyle \varepsilon }$ durch die Kegelspitze und die Gerade ${\displaystyle g}$. ${\displaystyle \varepsilon }$ schneidet den Kegel in zwei Mantellinien (Geraden) ${\displaystyle a,b}$. Der Schnitt von ${\displaystyle a}$ und ${\displaystyle b}$ mit der Gerade ${\displaystyle g}$ liefert die gesuchten Schnittpunkte.

Durchführung der Konstruktion:

1. Zur Bestimmung der Grundrissspur ${\displaystyle s}$ der Ebene ${\displaystyle \varepsilon }$ benötigt man zwei Spurpunkte. Als ersten Punkt wurde im Beispiel (siehe Bild) die Grundrissspur der Gerade ${\displaystyle g}$ bestimmt. Einen zweiten Spurpunkt ${\displaystyle V}$ erhält man mit Hilfe einer in der Ebene ${\displaystyle \varepsilon }$ liegenden Hilfsgerade ${\displaystyle h}$.
2. Die Schnittpunkte der Grundrissspur ${\displaystyle s}$ mit dem Bodenkreis des Kegels liefert Punkte ${\displaystyle R,T}$, die sowohl auf dem Kegel als auch in der Ebene ${\displaystyle \varepsilon }$ liegen. Die Geraden ${\displaystyle {\overline {SR}},{\overline {ST}}}$ sind also die Mantellinien ${\displaystyle a,b}$ und deren Schnitte mit ${\displaystyle g}$ die gesuchten Schnittpunkte (Durchdringungspunkte) ${\displaystyle A,B}$. Im Beispiel erhält man zunächst die Grundrisse ${\displaystyle A',B'}$ und als Schnittpunkte der zugehörigen Ordner mit ${\displaystyle g''}$ die Aufrisse ${\displaystyle A'',B''}$.

• Darstellende Geometrie für Architekten (PDF; 1,5 MB). Skript (Uni Darmstadt), S. 35, 73, 74.

• Rudolf Fucke, Konrad Kirch, Heinz Nickel: Darstellende Geometrie. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4, S. 34, 86, 87.
• Ulrich Graf, Martin Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9, S. 70, 230.
• C. Leopold: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X, S. 92