Duale Netzwerke

Duale Netzwerke bzw. duale Schaltungen sind elektrische Netzwerke, in denen Ströme und Spannungen vertauscht sind.^[1]

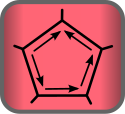
Duale Topologie

(c) Cobalt pen, CC BY-SA 3.0

duale Graphen

Im Kontext der Graphentheorie lässt sich für den Fall ebener Graphen ein Dualitätsbegriff fassen, der eng mit der Beziehung von Zyklen- und Schnittraum eines Graphen verwandt ist.^[2] Wie in nebenstehender Skizze dargestellt, entsprechen die Kanten beider Graphen ein-eindeutig einander, während die Knoten des einen Graphen im anderen als Zyklen auftreten und umgekehrt. In Begriffen der Elektrotechnik werden die Zyklen als Maschen, die Kanten als Zweige mit je einem Zweipol, der Graph als Netzwerk oder, mit Fokus auf den graphentheoretischen Hintergrund, als Topologie bezeichnet.

Duale Elemente und Gesetzmäßigkeiten

Zweipole sind dann dual zueinander, wenn ihre Strom-Spannungs-Kennlinien bei Vertauschen von Spannung und Strom strukturell erhalten bleibt. Dies ist insbesondere bei Impedanzen mit ${\displaystyle Z'=1/Z}$ der Fall. Damit stehen sich Grundelemente wie Quellen und Impedanzen wie folgt dual gegenüber.

Element	${\displaystyle Z}$	Dual	${\displaystyle Z'}$
Stromquelle	${\displaystyle \infty }$	Spannungsquelle	${\displaystyle 0}$
Widerstand	${\displaystyle R={\frac {1}{G}}}$	Leitwert	${\displaystyle G={\frac {1}{R}}}$
Induktivität	${\displaystyle \mathrm {j} \omega L}$	Kapazität	${\displaystyle {\frac {1}{\mathrm {j} \omega C}}}$

Darüber hinausgehend lässt sich die Dualität auch bei gesetzmäßigen Zusammenhängen und den dabei auftretenden Größen angeben:

Hinweis: Die Korrespondenzen gelten natürlich auch in Gegenrichtung, das heißt, das Dual des in der rechten Spalte Aufgeführten findet sich in der linken Spalte.

Duale Netzwerke

Zwei Netzwerke sind dual zueinander, wenn

• ihre Topologie dual ist.
• alle korrespondierenden Zweipole dual sind.

Beispiele

(c) Cobalt pen, CC BY-SA 3.0

Dualität von Reihen- und Parallelschaltung

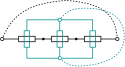
Reihen- und Parallelschaltung

Die nebenstehende Skizze zeigt die graphische Konstruktion der Dualität von Reihen- und Parallelschaltung von Impedanzen. Da die Schaltung nicht geschlossen ist, wurden die Anschlüsse hilfsweise mit den gestrichelten Linien verbunden. Man vergewissere sich, dass jeder Zweipol sein korrespondierendes Dual hat und jeder Knoten genau in einer Masche der dualen Schaltung liegt. Ferner ist jede der dualen Schaltungen für sich planar, enthält also keine sich kreuzenden Verbindungen.

Einzelnachweise

1. ↑ Kories, Schmidt-Walter: Taschenbuch der Elektrotechnik, Grundlagen und Elektronik, 9. Auflage, 2010, ISBN 978-3-8171-1858-8. S. 145ff.
2. ↑ Diestel: Graphentheorie. 3. Auflage, 2006, ISBN 978-3-540-21391-8. S. 113ff