Donald Newmans Beweis des Primzahlsatzes

Donald Newmans Beweis des Primzahlsatzes stammt aus dem Jahr 1972 und benutzt primär Mittel der Funktionentheorie. Das Manuskript von Donald Newman mit dem Titel Simple analytic proof of the prime number theorem erschien 1980 im American Mathematical Monthly. Der Beweis ist bekannt durch seine besondere Kürze und damit relativ hohe Zugänglichkeit.

Der Primzahlsatz trifft eine Aussage über die asymptotische Häufigkeitsverteilung von Primzahlen. Erstmals bewiesen wurde er im Jahr 1896, unabhängig von Jacques Hadamard und Charles-Jean de La Vallée Poussin. Deren Beweise verwendeten ebenfalls funktionentheoretische Mittel, gelten jedoch als aufwändig und überholt. Zwar wurden im Jahr 1948 sogenannte „elementare“ Beweise des Primzahlsatzes von Atle Selberg und Paul Erdös gegeben, wofür Selberg 1950 unter anderem die Fields-Medaille erhielt, jedoch bezieht sich diese Bezeichnung nur auf die ohne Funktionentheorie auskommende Methodik und nicht den Schwierigkeitsgrad.

Zum vollen Verständnis des Beweises von Newman sind lediglich Grundlagen aus der Analysis (wie Konvergenz von Reihen und Produkten, Ungleichungen, Differential- und Integralrechnung), der elementaren Zahlentheorie (wie Primzahlen und Teilbarkeit) und der Funktionentheorie (wie holomorphe Funktionen, die Cauchysche Integralformel und Weierstraßscher Konvergenzsatz) vonnöten. Ferner wurde er in verschiedene Standardwerke zur Funktionentheorie übernommen, etwa bei Theodore W. Gamelin und Serge Lang.

Der Primzahlsatz

Bereits seit der Antike ist bekannt, dass es unendlich viele Primzahlen gibt, weshalb die Liste 2, 3, 5, 7, 11, 13, … niemals endet. Der erste Beweis dieser Aussage stammt von Euklid, weshalb das Ergebnis auch Satz des Euklid genannt wird.

Die bloße Unendlichkeit einer Teilmenge der natürlichen Zahlen sagt noch nicht allzu viel über deren Natur aus. Zum Beispiel gibt es unendlich viele gerade Zahlen 2, 4, 6, 8 … und unendlich viele Quadratzahlen 1, 4, 9, 16 …, jedoch weisen beide Folgen bei genauem Hinsehen ein unterschiedliches Verhalten auf. Während zum Beispiel die Differenz zweier aufeinanderfolgender gerader Zahlen stets 2 ist, nehmen die Abstände der Quadratzahlen immer weiter zu, etwa 4 − 1 = 3, 9 − 4 = 5 und 16 − 9 = 7. Beide Folgen haben jedoch ein sehr reguläres Muster gemein, d. h., sie können über einfache Rechenoperationen bestimmt werden. Zum Beispiel ist die n-te gerade Zahl einfach 2n. Im Gegensatz dazu ist bis heute kein einfaches Muster unter der Folge 2, 3, 5, 7, 11, …, 59, 61, 67, … der Primzahlen entdeckt worden. Zum Beispiel gibt es kein „schnelles“ Verfahren, die n-te Primzahl zu berechnen. Die genaue Natur der Primzahlen ist bis heute ein bedeutendes offenes Problem.

Es zeigt sich jedoch, dass es auf lange Sicht Muster unter den Primzahlen zu erkennen gibt. Betrachtet man also haufenweise Primzahlen zur gleichen Zeit, so können durch „Mittelwertbildung“ reguläre Strukturen erkannt werden. Das Prinzip hinter dieser Tatsache ist von statistischer Natur. Statistik bedeutet hierbei, aus einer großen Menge von Daten Muster herauszufiltern, obwohl das „exakte Verhalten“ der einzelnen Datenobjekte (oder Subjekte) sehr kompliziert sein kann. So sind etwa alle Menschen sehr komplex, doch im Verhalten sehr vieler Menschen zur gleichen Zeit können Muster oftmals erkannt werden, die dann in Form von Wahrscheinlichkeiten auf Individuen zurück schließen lassen. Also geht es bei diesen Überlegungen zunächst um die Frage, wie die Verteilung der Primzahlen zu verstehen ist, mit anderen Worten, wie viele Primzahlen unterhalb einer vorgegebenen Schranke zu erwarten sind. Zum Beispiel sind nur 4 Primzahlen, nämlich 2, 3, 5 und 7, kleiner als die Zahl 10. Im Falle der oberen Schranke 150 gibt es schon 35 kleinere Primzahlen, nämlich

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149.

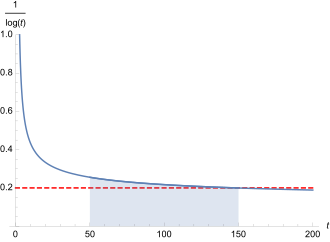
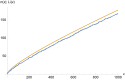
Dabei sind die insgesamt 20 Primzahlen zwischen 50 und 150 in grün markiert. Eine Frage der Zahlentheorie ist, ob es ein universelles und einfaches Prinzip gibt, zumindest zu schätzen, wie viele Primzahlen es unter einer gegebenen Schranke gibt. Erkannt wurde ein solches erstmals in den Jahren 1792/93 vom damals 15-jährigen Carl Friedrich Gauß,^[1] nachdem dieser Logarithmentafeln studiert hatte. Gauß vermutete, dass die Anzahl aller Primzahlen von 2 bis zu einer großen Zahl x ungefähr dem Flächeninhalt zwischen der t-Achse und der Funktion ${\displaystyle t\mapsto {\tfrac {1}{\log(t)}}}$ im Intervall von 2 bis ${\displaystyle x}$ entspricht. Dabei ist ${\displaystyle \log(t)}$ der natürliche Logarithmus. Es gilt also die Integral-Näherung^[2]

Anzahl der Primzahlen bis ${\displaystyle x}$ ${\displaystyle \approx \int _{2}^{x}{\frac {1}{\log(t)}}\mathrm {d} t}$

und allgemeiner für ${\displaystyle y>x\geq 2}$:

Anzahl der Primzahlen zwischen ${\displaystyle x}$ und ${\displaystyle y}$ ${\displaystyle \approx \int _{x}^{y}{\frac {1}{\log(t)}}\mathrm {d} t.}$

Zum Beispiel gilt

${\displaystyle \int _{50}^{150}{\frac {1}{\log(t)}}\mathrm {d} t=22{,}033\ldots ,}$

womit sich die Formel wegen des exakten Wertes von 20 Primzahlen zwischen 50 und 150 (siehe oben in grün) ca. um den Wert 2 verschätzt. Das Integral von ${\displaystyle {\tfrac {1}{\log(t)}}}$ kann nicht elementar geschlossen berechnet werden, da der Kehrwert des Logarithmus keine elementare Stammfunktion besitzt. Es definiert somit eine „eigenständige“ Funktion, die auch als Integrallogarithmus ${\displaystyle \operatorname {Li} }$ bekannt ist:

${\displaystyle \operatorname {Li} (x):=\int _{2}^{x}{\frac {1}{\log(t)}}\mathrm {d} t.}$

Bezeichnet ${\displaystyle \pi (x)}$ die exakte Anzahl der Primzahlen unterhalb der Schranke ${\displaystyle x}$, so wird die obere Aussage ${\displaystyle \pi (x)\approx \operatorname {Li} (x)}$ wie folgt präzisiert:

${\displaystyle \lim _{x\to \infty }{\frac {\pi (x)}{\operatorname {Li} (x)}}=1.}$

Für wachsende Werte von ${\displaystyle x}$ wird also der obige Quotient immer näher gegen 1 streben, also der relative Fehler der Schätzung ${\displaystyle \pi (x)\approx \operatorname {Li} (x)}$ gegen 0 gehen. Auch bei der „Statistik der Primzahlen“ gilt demnach der Grundsatz, dass größer werdende Datenmengen prozentual eine zuverlässigere Prognose erlauben. Gauß legte keinen mathematischen Beweis für diese Vermutung über die Primzahlverteilung vor, und es dauerte noch über 100 Jahre, bis ein solcher – unabhängig voneinander von Jacques Hadamard und Charles-Jean de La Vallée Poussin – im Jahr 1896 erbracht wurde.^[3] Dabei bedeutet Beweis nicht, dass alle erdenklichen Werte durchprobiert wurden, was bei unendlich vielen Zahlen unmöglich ist, sondern dass ein auf den mathematischen Axiomen basierendes logisches Argument den Sachverhalt in voller Allgemeinheit belegt. Das damit gezeigte Theorem wird als Primzahlsatz bezeichnet.^[2]

Der Beweis

Newmans Beweis kann in mehrere Schritte unterteilt werden. Anlässlich des 100. Beweisjahres des Primzahlsatzes wurden diese von Don Zagier in einem weiteren Artikel im American Mathematical Monthly zusammengestellt.

Schritt 1: Euler-Produkt der Riemannschen Zeta-Funktion

Für komplexe Zahlen ${\displaystyle s}$, deren Realteil größer als 1 ist, ist die Zeta-Funktion definiert durch die Dirichlet-Reihe^[4]

${\displaystyle \zeta (s):=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+{\frac {1}{4^{s}}}+{\frac {1}{5^{s}}}+{\frac {1}{6^{s}}}+{\frac {1}{7^{s}}}+\dotsb ,\,\,\,\,\,\,\,\,\,n^{s}:=\exp(s\log(n)).}$

Eine anschauliche Erklärung dieser Definition findet sich hier.

Wie man mittels des Integralkriteriums für unendliche Reihen zeigen kann, ist diese Reihe im angegebenen Bereich absolut konvergent. Zudem ist die Konvergenz auf kompakten Teilmengen gleichmäßig, weshalb nach dem Satz von Weierstraß die dargestellte Funktion holomorph ist. Wegen der Divergenz der harmonischen Reihe ist diese Darstellung für alle komplexen Zahlen mit Realteil kleiner oder gleich 1 jedoch ungültig. Sie kann aber zu einer in ganz ${\displaystyle \mathbb {C} \setminus \{1\}}$ holomorphen Funktion fortgesetzt werden.

Das Euler-Produkt ist eine alternative Darstellung der Zeta-Funktion im Konvergenzbereich der Dirichlet-Reihe. Als Formel geschrieben lautet es:

${\displaystyle \zeta (s)=\prod _{p\ {\text{Primzahl}}}{\frac {1}{1-{\frac {1}{p^{s}}}}}={\frac {1}{1-{\frac {1}{2^{s}}}}}\cdot {\frac {1}{1-{\frac {1}{3^{s}}}}}\cdot {\frac {1}{1-{\frac {1}{5^{s}}}}}\cdot {\frac {1}{1-{\frac {1}{7^{s}}}}}\cdot {\frac {1}{1-{\frac {1}{11^{s}}}}}\cdot {\frac {1}{1-{\frac {1}{13^{s}}}}}\cdot \cdots ,\quad }$ wobei ${\displaystyle \operatorname {Re} (s)>1}$.

Dabei ist ${\displaystyle \Pi }$ das Produktzeichen, und das rechte Produkt erstreckt sich über genau alle Primzahlen. Für unendliche Produkte (nach Euklid gibt es unendlich viele Primzahlen) gelten ähnliche Anschauungen wie für Reihen, nur dass die Faktoren („Glieder des Produktes“) im Laufe der Zeit gegen 1 streben müssen, falls das betroffene Produkt konvergieren soll, da Faktoren nahe 1, genau wie Summanden nahe 0, nur noch wenig am Zwischenwert ändern. Das Euler-Produkt ergibt sich aus der geometrischen Reihe sowie dem Fundamentalsatz der Arithmetik. Es ist andersherum eine analytische Formulierung der Tatsache, dass jede natürliche Zahl ${\displaystyle n}$ eine eindeutige Primfaktorzerlegung besitzt, wobei die Eindeutigkeit durch die ${\displaystyle 1}$ im Zähler des Terms ${\displaystyle {\tfrac {1}{n^{s}}}}$ innerhalb der Zeta-Reihe ausgedrückt wird.

Schritt 2: Fortsetzung der Zeta-Funktion

Als Nächstes muss gezeigt werden, dass die Funktion ${\displaystyle s\mapsto \zeta (s)-{\tfrac {1}{s-1}}}$ auf die Halbebene ${\displaystyle \mathrm {Re} (s)>0}$ fortgesetzt werden kann. Insbesondere hat ${\displaystyle \zeta (s)}$ einen einfachen Pol in ${\displaystyle s=1}$. Dies geht zum Beispiel über die zunächst nur für ${\displaystyle \mathrm {Re} (s)>1}$ gültige Identität

${\displaystyle \zeta (s)-{\frac {1}{s-1}}=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}-\int _{1}^{\infty }{\frac {\mathrm {d} x}{x^{s}}}=\sum _{n=1}^{\infty }\int _{n}^{n+1}\left({\frac {1}{n^{s}}}-{\frac {1}{x^{s}}}\right)\mathrm {d} x.}$

Über den Mittelwertsatz kann man zeigen, dass die rechte Reihe sogar für ${\displaystyle \mathrm {Re} (s)>0}$ gleichmäßig und absolut konvergiert auf kompakten Teilmengen, denn

${\displaystyle \sum _{n=1}^{\infty }\left|\int _{n}^{n+1}\left({\frac {1}{n^{s}}}-{\frac {1}{x^{s}}}\right)\mathrm {d} x\right|=\sum _{n=1}^{\infty }\left|s\int _{n}^{n+1}\left(\int _{n}^{x}{\frac {\mathrm {d} u}{u^{s+1}}}\right)\mathrm {d} x\right|\leq \sum _{n=1}^{\infty }\max _{n\leq u\leq n+1}\left|{\frac {s}{u^{s+1}}}\right|=\sum _{n=1}^{\infty }{\frac {|s|}{n^{\mathrm {Re} (s)+1}}}<\infty .}$

Damit ist die betrachtete Funktion wegen des Konvergenzsatzes von Weierstraß auf der Halbebene ${\displaystyle \mathrm {Re} (s)>0}$ holomorph.

Schritt 3: Beschränkung der Chebyshev-Funktion

Die erste Chebyshev-Funktion ist definiert durch

${\displaystyle \vartheta (x):=\sum _{p\leq x \atop p\,{\text{Primzahl}}}\log(p).}$

Es wird gezeigt, dass der Quotient ${\displaystyle {\tfrac {\vartheta (x)}{x}}}$ für ${\displaystyle x\to \infty }$ beschränkt ist. Um dies zu sehen, benutzt man zuerst den binomischen Lehrsatz:

${\displaystyle 2^{2n}=(1+1)^{2n}={\binom {2n}{0}}+\cdots +{\binom {2n}{2n}}\geq {\binom {2n}{n}}={\frac {(2n)!}{n!^{2}}}\geq \prod _{n<p\leq 2n \atop p\,{\text{Primzahl}}}p=e^{\vartheta (2n)-\vartheta (n)}.}$

Ändert man in ${\displaystyle \vartheta (x)}$ das Argument um einen beschränkten Term ${\displaystyle O(1)}$ ab, so gilt

${\displaystyle \vartheta (x+O(1))-\vartheta (x)=O(\log(x)).}$

Damit gilt mit obiger Ungleichung:

${\displaystyle \vartheta (x)-\vartheta \left({\frac {x}{2}}\right)\leq Cx}$

mit einem ${\displaystyle C>\log(2)}$ für alle ${\displaystyle x\geq x_{0}=x_{0}(C)}$. Damit folgt durch eine Teleskopsumme mit ${\displaystyle {\tfrac {x}{2^{R}}}\geq x_{0}>{\tfrac {x}{2^{R+1}}}}$:

${\displaystyle \vartheta (x)=\sum _{r=0}^{\infty }\left(\vartheta \left({\frac {x}{2^{r}}}\right)-\vartheta \left({\frac {x}{2^{r+1}}}\right)\right)\leq \sum _{r=0}^{R}\left(\vartheta \left({\frac {x}{2^{r}}}\right)-\vartheta \left({\frac {x}{2^{r+1}}}\right)\right)+O(1)\leq Cx\sum _{r=0}^{R}{\frac {1}{2^{r}}}+O(1)=O(x).}$

Schritt 4: Fortsetzbarkeit der reziproken Zeta-Funktion

Es ist zuerst zu zeigen, dass ${\displaystyle \zeta (s)\not =0}$ für alle ${\displaystyle \mathrm {Re} (s)\geq 1}$ gilt. Damit folgt schon mit Schritt 2, dass sich die Funktion ${\displaystyle s\mapsto {\tfrac {1}{\zeta (s)}}}$ holomorph nach ${\displaystyle \mathrm {Re} (s)\geq 1}$ fortsetzen lässt. Es ist mit dem Euler-Produkt bereits ${\displaystyle \zeta (s)\not =0}$ im gesamten Bereich ${\displaystyle \mathrm {Re} (s)>1}$. Der verbleibende Fall ${\displaystyle \mathrm {Re} (s)=1}$ lässt sich nun mit einem Satz von Franz Mertens behandeln, der zeigte, dass für ${\displaystyle a_{n}\geq 0}$ im Bereich der Konvergenz (${\displaystyle s=\sigma +it}$ mit ${\displaystyle \sigma ,t\in \mathbb {R} }$)

${\displaystyle 3\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{\sigma }}}+4\mathrm {Re} \left(\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{\sigma +it}}}\right)+\mathrm {Re} \left(\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{\sigma +2it}}}\right)=\sum _{n=1}^{\infty }{\frac {a_{n}(3+4\cos(t\log(n))+\cos(2t\log(n)))}{n^{\sigma }}}\geq 0,}$

denn es gilt ${\displaystyle 3+4\cos(\theta )+\cos(2\theta )=2(1+\cos(\theta ))^{2}\geq 0}$. Über das logarithmierte Euler-Produkt folgt für ${\displaystyle \sigma >1}$

${\displaystyle 3\log \zeta (\sigma )+4\mathrm {Re} (\log \zeta (\sigma +it))+\mathrm {Re} (\log \zeta (\sigma +2it))\geq 0,}$

denn

${\displaystyle \log \zeta (s)=-\sum _{p\,{\text{Primzahl}}}\log \left(1-{\frac {1}{p^{s}}}\right)=\sum _{n=2}^{\infty }{\frac {\Lambda (n)}{n^{s}\log(n)}}}$

mit der Mangoldt-Funktion ${\displaystyle \Lambda }$, und man hat ${\displaystyle {\tfrac {\Lambda (n)}{\log(n)}}\geq 0}$. Ergo ist

${\displaystyle \left|e^{3\log \zeta (\sigma )+4\mathrm {Re} (\log \zeta (\sigma +it))+\mathrm {Re} (\log \zeta (\sigma +2it))}\right|=\zeta (\sigma )^{3}|\zeta (\sigma +it)|^{4}|\zeta (\sigma +2it)|\geq 1,\qquad \sigma >1.}$

Wäre ${\displaystyle \zeta (1+it)=0}$ für ein reelles ${\displaystyle t\not =0}$, so wäre ${\displaystyle \lim _{\sigma \to 1}\zeta (\sigma )^{3}|\zeta (\sigma +it)|^{4}|\zeta (\sigma +2it)|=0}$ (denn der – siehe Schritt 2 – einfache Pol in ${\displaystyle \sigma =1}$ wird nur dreifach gewertet), was ein Widerspruch ist.

Mit diesem Nichtverschwindungsresultat wird nun argumentiert, dass sich die Funktion ${\displaystyle s\mapsto \Phi (s)-{\tfrac {1}{s-1}}}$ mit

${\displaystyle \Phi (s):=\sum _{p\,{\text{Primzahl}}}{\frac {\log(p)}{p^{s}}}={\frac {\log(2)}{2^{s}}}+{\frac {\log(3)}{3^{s}}}+{\frac {\log(5)}{5^{s}}}+\cdots }$

holomorph auf die Halbebene ${\displaystyle \mathrm {Re} (s)\geq 1}$ fortsetzen lässt. Dafür wird die aus der logarithmischen Ableitung des Euler-Produktes gewonnene Identität

${\displaystyle -{\frac {\zeta '(s)}{\zeta (s)}}=\sum _{p\,{\text{Primzahl}}}{\frac {\log(p)}{p^{s}-1}}=\Phi (s)+\sum _{p\,{\text{Primzahl}}}{\frac {\log(p)}{p^{s}(p^{s}-1)}}}$

genutzt. Die Funktion ${\displaystyle s\mapsto -{\tfrac {\zeta '(s)}{\zeta (s)}}-{\tfrac {1}{s-1}}}$ dehnt sich nach dem Nichtverschwindungssatz und Schritt 2, und die Reihe ${\displaystyle \textstyle s\mapsto \sum _{p\,{\text{Primzahl}}}{\frac {\log(p)}{p^{s}(p^{s}-1)}}}$ wegen gleichmäßiger Konvergenz auf Kompakta in ${\displaystyle \mathrm {Re} (s)>{\tfrac {1}{2}}}$, holomorph auf ${\displaystyle \mathrm {Re} (s)\geq 1}$ aus.

Schritt 5: Konvergenz des Integrals mit der Chebyshev-Funktion

Es wird gezeigt, dass das Integral

${\displaystyle \int _{1}^{\infty }{\frac {\vartheta (x)-x}{x^{2}}}\mathrm {d} x=\int _{0}^{\infty }(e^{-t}\vartheta (e^{t})-1)\mathrm {d} t}$

konvergiert. Dafür schreibt man die Funktion ${\displaystyle \Phi }$ als Laplace-Transformierte der Chebyshev-Funktion mit exponentiellem Argument:

${\displaystyle \Phi (s)=\sum _{p\,{\text{Primzahl}}}{\frac {\log(p)}{p^{s}}}=s\int _{1}^{\infty }{\frac {\vartheta (x)}{x^{s+1}}}\mathrm {d} x=s\int _{0}^{\infty }\vartheta (e^{t})e^{-st}\mathrm {d} t.}$

Ergo ist

${\displaystyle {\frac {\Phi (s+1)}{s+1}}-{\frac {1}{s}}=\int _{0}^{\infty }(e^{-t}\vartheta (e^{t})-1)e^{-st}\mathrm {d} t.}$

Die Behauptung folgt nun mit Schritten 3, 4 und dem folgenden

Taubersatz von Newman: Es sei ${\displaystyle f(t)}$ mit ${\displaystyle t\geq 0}$ eine beschränkte, lokal integrierbare Funktion. Es sei angenommen, die auf ${\displaystyle \mathrm {Re} (s)>0}$ holomorphe Funktion

${\displaystyle g(s):=\int _{0}^{\infty }f(t)e^{-st}\mathrm {d} t}$

dehne sich holomorph auf ${\displaystyle \mathrm {Re} (s)\geq 0}$ aus. Dann konvergiert ${\displaystyle \textstyle \int _{0}^{\infty }f(t)\mathrm {d} t}$ und hat den Wert ${\displaystyle g(0)}$.

Schritt 6: Asymptotisches Verhalten der Chebyshev-Funktion

Es wird ${\displaystyle \vartheta (x)\sim x}$ für ${\displaystyle x\to \infty }$ gezeigt. Das funktioniert zum Beispiel über einen Widerspruchsbeweis. Mit der Konvergenz des Integrals ${\displaystyle \textstyle \int _{0}^{\infty }{\tfrac {\vartheta (x)-x}{x^{2}}}\mathrm {d} x}$ folgt

${\displaystyle \lim _{T\to \infty }\int _{T}^{\lambda T}{\frac {\vartheta (x)-x}{x^{2}}}\mathrm {d} x=0}$

für alle ${\displaystyle \lambda >0}$. Ist nun ${\displaystyle \lambda >1}$ und ${\displaystyle \vartheta (T)\geq \lambda T}$ für beliebig groß werdende ${\displaystyle T}$, so folgt, da ${\displaystyle \vartheta }$ nicht fallend ist,

${\displaystyle \int _{T}^{\lambda T}{\frac {\vartheta (x)-x}{x^{2}}}\mathrm {d} x\geq \int _{T}^{\lambda T}{\frac {\lambda T-x}{x^{2}}}\mathrm {d} x=\int _{1}^{\lambda }{\frac {\lambda -x}{x^{2}}}\mathrm {d} x>0}$

und der letzte Wert hängt nicht von ${\displaystyle T}$ ab, ein Widerspruch. Ähnlich wird mit ${\displaystyle \lambda <1}$ argumentiert: Ist ${\displaystyle \vartheta (T)\leq \lambda T}$, so gilt

${\displaystyle \int _{\lambda T}^{T}{\frac {\vartheta (x)-x}{x^{2}}}\mathrm {d} x\leq \int _{\lambda T}^{T}{\frac {\lambda T-x}{x^{2}}}\mathrm {d} x=\int _{\lambda }^{1}{\frac {\lambda -x}{x^{2}}}\mathrm {d} x<0.}$

Auch dies führt zu einem Widerspruch.

Schritt 7: Beweis des Primzahlsatzes

Mit Schritt 6 kann nun der Primzahlsatz bewiesen werden. Es gilt einerseits folgende Abschätzung nach oben:

${\displaystyle \vartheta (x)=\sum _{p\leq x}\log(p)\leq \sum _{p\leq x}\log(x)=\pi (x)\log(x).}$

Auf der anderen Seite hat man für jedes ${\displaystyle \varepsilon >0}$ folgende Abschätzung nach unten:

${\displaystyle \vartheta (x)\geq \sum _{x^{1-\varepsilon }\leq p\leq x}\log(p)\geq \sum _{x^{1-\varepsilon }\leq p\leq x}(1-\varepsilon )\log(x)=(1-\varepsilon )\log(x)\left(\pi (x)+O(x^{1-\varepsilon })\right).}$

Daraus folgt ${\displaystyle \vartheta (x)\sim \log(x)\pi (x)\sim x}$, also ${\displaystyle \pi (x)\sim {\tfrac {x}{\log(x)}}}$.

Appendix: Beweis des Taubersatzes

Für ${\displaystyle T>0}$ wird

${\displaystyle g_{T}(s):=\int _{0}^{T}f(t)e^{-st}\mathrm {d} t}$

definiert. Dies ist holomorph für alle ${\displaystyle s}$. Es genügt, ${\displaystyle \lim _{T\to \infty }g_{T}(0)=g(0)}$ zu zeigen. Für große ${\displaystyle R>0}$ bezeichne ${\displaystyle C}$ den Rand des abgeschnittenen Kreises ${\displaystyle \{s\in \mathbb {C} :|s|\leq R,\mathrm {Re} (s)\geq -\delta \}}$, wobei ${\displaystyle \delta >0}$ abhängig von ${\displaystyle R}$ klein genug gewählt ist, sodass ${\displaystyle g}$ holomorph in ganz ${\displaystyle C}$ ist (siehe auch Lebesguezahl). Es ist dabei zu beachten, dass Holomorphie in einem (Rand-)Punkt stets in eine Umgebung dieses Punktes ausstrahlt, etwa wegen der vorhandenen Taylor-Entwicklung. Mit der Cauchyschen Integralformel folgt

${\displaystyle g(0)-g_{T}(0)={\frac {1}{2\pi i}}\int _{C}(g(s)-g_{T}(s))e^{sT}\left(1+{\frac {s^{2}}{R^{2}}}\right){\frac {\mathrm {d} s}{s}},}$

wobei der Term ${\displaystyle {\tfrac {s^{2}}{R^{2}}}}$ die Funktion einer komplizierten Null innehat und ${\displaystyle e^{0}=1}$ zu beachten ist. Es wird nun argumentiert, dass dieses Integral für ${\displaystyle T\to \infty }$ gegen 0 strebt. Auf dem Halbkreis ${\displaystyle C_{+}:=C\cap \{\mathrm {Re} (s)>0\}}$ ist der Integrand durch ${\displaystyle {\tfrac {2B}{R^{2}}}}$ beschränkt, wobei ${\displaystyle B:=\max _{t\geq 0}|f(t)|}$, denn einerseits gilt

${\displaystyle |g(s)-g_{T}(s)|=\left|\int _{T}^{\infty }f(t)e^{-st}\mathrm {d} t\right|\leq B\int _{T}^{\infty }\left|e^{-st}\right|\mathrm {d} t={\frac {Be^{-\mathrm {Re} (s)T}}{\mathrm {Re} (s)}},}$

und andererseits

${\displaystyle \left|e^{sT}\left(1+{\frac {s^{2}}{T^{2}}}\right){\frac {1}{s}}\right|=e^{\mathrm {Re} (s)T}\cdot {\frac {2\mathrm {Re} (s)}{R^{2}}}.}$

Nach der Standardabschätzung für Wegintegrale ist der Beitrag des Integrals über ${\displaystyle C_{+}}$ an ${\displaystyle g(0)-g_{T}(0)}$ durch ${\displaystyle {\tfrac {B}{R}}}$ beschränkt. Für den Kurventeil ${\displaystyle C_{-}:=C\cap \{\mathrm {Re} (s)<0\}}$ werden ${\displaystyle g}$ und ${\displaystyle g_{T}}$ separat betrachtet. Da ${\displaystyle g_{T}}$ eine ganze Funktion ist, kann der Weg ${\displaystyle C_{-}}$ hier zum Halbkreis ${\displaystyle C\cap \{\mathrm {Re} (s)<0\}}$ deformiert werden, ohne dessen Wert zu verändern, und auf dieser neuen Kurve gilt die Beschränkung durch ${\displaystyle {\tfrac {B}{R}}}$, denn nach gleicher Argumentation wie oben gilt

${\displaystyle |g_{T}(s)|=\left|\int _{0}^{T}f(t)e^{-st}\mathrm {d} t\right|\leq B\int _{-\infty }^{T}|e^{-st}|\mathrm {d} t={\frac {Be^{-\mathrm {Re} (s)T}}{|\mathrm {Re} (s)|}}.}$

Zu guter Letzt geht das verbliebene Integral über ${\displaystyle C_{-}}$ für ${\displaystyle T\to \infty }$ gegen 0, denn der Integrand ist das Produkt von ${\displaystyle g(s)(1+{\tfrac {s^{2}}{R^{2}}}){\tfrac {1}{s}}}$, was unabhängig von ${\displaystyle T}$ ist, mit ${\displaystyle e^{Ts}}$, was auf kompakten Teilmengen der Halbebene ${\displaystyle \{\mathrm {Re} (s)<0\}}$ schnell und gleichmäßig gegen 0 strebt. Daraus folgt

${\displaystyle \limsup _{T\to \infty }|g(0)-g_{T}(0)|\leq {\frac {2B}{R}}}$

und mit der beliebigen Wahl ${\displaystyle R\to \infty }$ die Behauptung.

Literatur

• Donald Newman: A simple proof of the prime number theorem. American Mathematical Monthly, Band 87, 1980, S. 693–696.
• Don Zagier: Newman’s short proof of the prime number theorem. In: The American Mathematical Monthly, Band 104, Nr. 8 (Oktober 1997), S. 705–708 (PDF).

Einzelnachweise

1. ↑ Carl Friedrich Gauß. Werke. Zweiter Band. Herausgegeben von der königlichen Gesellschaft der Wissenschaften zu Göttingen, 1863, (Brief), S. 444–447.
2. ↑ ^{a b} Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 41.
3. ↑ Władysław Narkiewicz: The Development in Prime Number Theory. Springer Monographs in Mathematics, S. 183.
4. ↑ E. Freitag, R. Busam: Funktionentheorie 1. Springer; 4. Aufl. 2006, ISBN 978-3-540-31764-7, S. 432.