Satz von Dirichlet (Primzahlen)

Der Satz von Dirichlet, gelegentlich auch Dirichletscher Primzahlsatz, benannt nach Peter Gustav Lejeune Dirichlet, ist eine Aussage aus dem mathematischen Teilgebiet der Zahlentheorie. Er besagt, dass eine aufsteigende arithmetische Progression unendlich viele Primzahlen enthält, wenn dies nicht aus trivialen Gründen, etwa bei ${\displaystyle 2,4,6,8,\dots }$, unmöglich ist. Eine arithmetische Progression ist dabei eine Folge ganzer Zahlen, sodass zwei aufeinanderfolgende Glieder stets dieselbe Differenz haben, wie zum Beispiel ${\displaystyle 1,4,7,10,13,\dots }$ Ganz allgemein ist eine solche Folge für eine ganze Zahl ${\displaystyle a}$ und eine natürliche Zahl ${\displaystyle N}$ gegeben durch

${\displaystyle a,a+N,a+2N,a+3N,\ldots }$

Die Folge ist dann im Sinne des Satzes von Dirichlet „trivial“, wenn ${\displaystyle a}$ und ${\displaystyle N}$ einen gemeinsamen Teiler haben, der größer als ${\displaystyle 1}$ ist. Den ersten vollständigen Beweis der Aussage lieferte Dirichlet im Jahr 1837. Dabei wurden erstmals rein analytische Methoden für die Gewinnung eines zahlentheoretischen Satzes verwendet. Die Vermutung über Primzahlen in arithmetischen Folgen stammt von Adrien-Marie Legendre aus dem Jahr 1798, der in seinem Lehrbuch der Zahlentheorie einen fehlerhaften Beweis gab, wie Dirichlet darlegte. Anwendung findet der Satz innerhalb der Zahlentheorie, etwa im Beweis des Satzes von Hasse-Minkowski.

Bezogen auf das Dezimalsystem sagt der Satz aus, dass es jeweils unendlich viele Primzahlen gibt, die auf eine 1, auf eine 3, auf eine 7 und auf eine 9 enden. Allgemeiner kann man sagen: Gibt es zwei verschiedene Primzahlen, die in einem Zahlensystem auf die gleiche Ziffernfolge enden, so gibt es unendlich viele weitere Primzahlen, die in diesem Zahlensystem auf diese Ziffernfolge enden. Etwa gibt es unendlich viele Primzahlen, die auf die Ziffern 419 enden. Die ersten Primzahlen mit dieser Eigenschaft sind ${\displaystyle 419,5419,8419,}$ und ${\displaystyle 9419}$.

Dirichlets Beweis war ein wichtiger Schritt zur Begründung der analytischen Zahlentheorie und führte zur Etablierung der Dirichletschen L-Funktionen, der Dirichlet-Charaktere und der analytischen Klassenzahlformel für quadratische Zahlkörper. Die Einführung der L-Funktion geschah in Analogie zu Leonhard Eulers Einführung der Zetafunktion bei der Primzahlverteilung. Tatsächlich konnte Dirichlet eine etwas stärkere Formulierung als die bloße Unendlichkeitsaussage gewinnen, denn er lieferte eine Verallgemeinerung des Satzes von Euler über Primzahlen: Addiert man also die Kehrwerte ${\displaystyle {\tfrac {1}{p}}}$ aller Primzahlen ${\displaystyle p}$ in der betroffenen arithmetischen Progression, ist das Ergebnis Unendlich. Diese Aussage impliziert die Unendlichkeit der entsprechenden Primzahlmenge, aber es existieren ganz allgemein unendlich lange Zahlfolgen, die in ihrer Kehrwertsumme beschränkt sind. Dirichlet zeigte dafür als entscheidenden Zwischenschritt das Nicht-Verschwinden der Dirichletschen L-Funktion an der Stelle ${\displaystyle 1}$. Hierbei wurde die Bedeutung des Nullstellenverhaltens von L-Funktionen in Form sog. Nichtverschwindungssätze für die Zahlentheorie erstmals offenkundig.

Im Laufe der Zeit konnte der Satz immer weiter verbessert werden. So schätzt etwa der Primzahlsatz für arithmetische Progressionen die genaue Anzahl der Primzahlen in einer arithmetischen Folge, die eine obere Schranke nicht überschreiten. Eine Folgerung ist, dass bei fester Wahl von ${\displaystyle N}$ in unterschiedlichen Folgen stets asymptotisch gleich viele Primzahlen liegen. Der Fehlerterm in dieser beschriebenen Primzahlverteilung ist Gegenstand des Satzes von Siegel-Walfisz, des Satzes von Bombieri und Winogradow und der Vermutung von Elliott und Halberstam. Unter Annahme der verallgemeinerten Riemannschen Vermutung kann dieser Fehler zudem sehr deutlich verbessert werden.

Notation

Es werden durchweg folgende Bezeichnungen verwendet:

• ${\displaystyle \mathbb {N} }$, ${\displaystyle \mathbb {Z} }$, ${\displaystyle \mathbb {Q} }$, ${\displaystyle \mathbb {R} }$ und ${\displaystyle \mathbb {C} }$ bezeichnen die natürlichen, ganzen, rationalen, reellen bzw. komplexen Zahlen.
• Die Notation für asymptotische Beschränktheit durch Landau-Symbole: Es bedeutet ${\displaystyle f(x)=O(g(x))}$, dass ${\displaystyle \limsup _{x\to a}\left|{\tfrac {f(x)}{g(x)}}\right|<\infty }$ (wobei meist ${\displaystyle a=\infty }$). Analog wird ${\displaystyle f(x)\ll g(x)}$ mit ${\displaystyle x\to a}$ gebraucht. Ferner bedeutet ${\displaystyle f(x)=o(g(x))}$ sogar ${\displaystyle \limsup _{x\to a}\left|{\tfrac {f(x)}{g(x)}}\right|=0}$. Es bezeichnet hierbei ${\displaystyle \limsup }$ den Limes superior. Es bedeutet ${\displaystyle f(x)\sim g(x)}$ für ${\displaystyle x\to a}$ schließlich

${\displaystyle \lim _{x\to a}{\tfrac {f(x)}{g(x)}}=1.}$

• Das Symbol ${\displaystyle \lim \limits _{x\to 1^{+}}}$ bedeutet, dass sich ${\displaystyle x}$ dem Wert 1 unter der Bedingung ${\displaystyle x>1}$ nähert und ihm beliebig nahe kommt, etwa durch ${\displaystyle 1{,}1;1{,}01;1{,}0001;\dots }$
• Es bezeichnen durchgängig ${\displaystyle \operatorname {Re} (z)}$ und ${\displaystyle \operatorname {Im} (z)}$ den Real- bzw. Imaginärteil der komplexen Zahl ${\displaystyle z}$.
• Wie üblich ist durchgängig ${\displaystyle \log(x)}$ der natürliche Logarithmus von ${\displaystyle x}$, und ${\displaystyle e^{x}}$ die natürliche Exponentialfunktion. Es bezeichnen ${\displaystyle \mathrm {Li} (x)}$ den Integrallogarithmus und ${\displaystyle \pi (x)}$ die Primzahl zählende Funktion. Allgemeiner ist ${\displaystyle \pi (x;N,l)}$ die Anzahl aller Primzahlen ${\displaystyle p\leq x}$, sodass ${\displaystyle p-l}$ durch ${\displaystyle N}$ teilbar ist. Teilt die Zahl ${\displaystyle d}$ die Zahl ${\displaystyle N}$, so wird dies mit ${\displaystyle d|N}$ notiert.
• Es bedeutet die Schreibweise ${\displaystyle a\equiv b{\pmod {N}}}$, dass ${\displaystyle N|(a-b)}$, dass also ${\displaystyle N}$ die Zahl ${\displaystyle a-b}$ teilt, siehe auch Modulo.
• Es bezeichnet ${\displaystyle \zeta (s)}$ die Riemannsche Zeta-Funktion. Zudem wird ${\displaystyle s=\sigma +it}$ mit reellen ${\displaystyle \sigma }$ und ${\displaystyle t}$ geschrieben.
• Es bezeichnet ${\displaystyle \varphi (n)}$ die Eulersche Phi-Funktion.
• Es bezeichnet ${\displaystyle \textstyle \sum }$ das Summenzeichen und ${\displaystyle \textstyle \prod }$ das Produktzeichen.

Aussage des Satzes

Primzahlen

Im Zentrum der Zahlentheorie, jenes Zweiges der Mathematik, der sich mit den Eigenschaften der natürlichen Zahlen 1, 2, 3, 4, … beschäftigt, stehen die Primzahlen 2, 3, 5, 7, 11, … Diese sind ausgezeichnet durch die Eigenschaft, genau zwei Teiler zu haben, nämlich die 1 und sich selbst. Die 1 ist keine Primzahl. Primzahlen bilden gewissermaßen die Atome der ganzen Zahlen, da sich jede positive ganze Zahl eindeutig multiplikativ in solche zerlegen lässt. Dieses Resultat wird auch als Fundamentalsatz der Arithmetik bezeichnet. Zum Beispiel gilt ${\displaystyle 21=3\cdot 7}$ und ${\displaystyle 110=2\cdot 5\cdot 11}$.

Trotz ihrer einfachen Definition ist nach mehreren Jahrtausenden Mathematikgeschichte bis heute kein Muster bekannt, dem sich die Primzahlen in ihrer Folge unterwerfen. Ihre Natur ist eine der bedeutendsten offenen Fragen der Mathematik. In der modernen Mathematik gibt es jedoch tiefliegende Vermutungen, die das Verhalten der Primzahlen als pseudozufällig einordnen und Verbindungen zur Quantenphysik sehen. All diese Aussagen liegen im Themenbereich der Riemannschen Vermutung.

Der Satz von Dirichlet

Eine arithmetische Progression ist eine Folge von ganzen Zahlen, wobei die Differenz zweier aufeinanderfolgender Zahlen konstant ist. Beispiele sind

${\displaystyle 1,5,9,13,17,21,\dots }$

oder auch

${\displaystyle 17,117,217,317,\dots }$

Der Satz von Dirichlet besagt, dass eine arithmetische Progression stets unendlich viele Primzahlen beinhaltet, es sei denn, dies ist aus trivialen Gründen unmöglich. In der einfachsten Fassung lautet der Satz:

Es sei ${\displaystyle N}$ eine natürliche Zahl und ${\displaystyle a}$ eine zu ${\displaystyle N}$ teilerfremde natürliche Zahl. Dann enthält die arithmetische Progression ${\displaystyle a,a+N,a+2N,a+3N,\ldots }$ unendlich viele Primzahlen.^[1]

Anders formuliert: Es gibt unendlich viele Primzahlen, die kongruent zu ${\displaystyle a}$ modulo ${\displaystyle N}$ sind. Dabei ist die Voraussetzung der Teilerfremdheit notwendig. Wären ${\displaystyle a}$ und ${\displaystyle N}$ nicht teilerfremd und ${\displaystyle g>1}$ ein gemeinsamer Teiler, so wäre jedes Folgenglied durch ${\displaystyle g}$ teilbar; zwei verschiedene Primzahlen können aber nicht beide durch ${\displaystyle g}$ teilbar sein. Dass die Bedingung der Teilerfremdheit von ${\displaystyle a}$ und ${\displaystyle N}$ für die Existenz unendlich vieler Primzahlen in der entsprechenden Folge nicht nur notwendig, sondern auch hinreichend ist, ist genau die Aussage des Satzes von Dirichlet. Dirichlet konnte sogar etwas mehr zeigen. Es handelt sich um eine direkte Verallgemeinerung des Satzes von Euler über Primzahlen. Es gilt mit oberen Bedingungen:^[1]

${\displaystyle \sum _{p\ {\text{Primzahl}} \atop p\equiv a{\pmod {N}}}{\frac {1}{p}}=\infty .}$

Diese Aussage ist stärker als die obere Version. Denn offenbar impliziert die Divergenz der Reihe die Unendlichkeit der Primzahlen in der betroffenen arithmetischen Folge. Es gibt allerdings unendliche Folgen, deren Kehrwertsumme beschränkt bleibt. Ein Beispiel bilden die Quadratzahlen (siehe Basler Problem), oder die Zweierpotenzen, es gilt

${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots =2<\infty .}$

Damit besagt die verstärkte Fassung des Satzes von Dirichlet, dass die Primzahlen in den relevanten arithmetischen Progressionen gewissermaßen „dicht“ unter den natürlichen Zahlen verteilt sind.

Beispiele

Aus dem Satz von Dirichlet folgt zum Beispiel, dass unendlich viele Primzahlen auf die Ziffern 1, 3, 7 oder 9 enden. Noch allgemeiner gibt es unendlich viele Primzahlen, deren letzte Ziffern auf 37, 113, 419 oder 567241 enden. Die ersten Primzahlen mit Endziffern 419 sind ${\displaystyle 419,5419,8419,9419,14419,17419}$. Es gilt ferner

${\displaystyle {\frac {1}{419}}+{\frac {1}{5419}}+{\frac {1}{8419}}+{\frac {1}{9419}}+{\frac {1}{14419}}+{\frac {1}{17419}}+\cdots =\infty .}$

Triviale Gründe, wann der Satz nicht gilt, liegen vor, wenn ${\displaystyle a}$ und ${\displaystyle N}$ nicht teilerfremd sind. Dann gibt es eine ganze Zahl ${\displaystyle d>1}$, die sowohl ${\displaystyle a}$ als auch ${\displaystyle N}$ teilt. Damit teilt ${\displaystyle d}$ jede der Zahlen ${\displaystyle a+kN}$ mit natürlichen ${\displaystyle k}$ und somit enthält diese Folge höchstens (einmal) die Primzahl ${\displaystyle d}$, falls ${\displaystyle d}$ überhaupt prim ist. Etwa sind ${\displaystyle a=8}$ und ${\displaystyle N=12}$ nicht teilerfremd. In der Tat sind alle Zahlen der Progression

${\displaystyle 8,20,32,44,\dots }$

durch ${\displaystyle 4=\operatorname {ggT} (8,12)}$ teilbar. Damit enthält sie keine einzige Primzahl.

Trivialerweise impliziert der Satz von Dirichlet den Satz des Euklid, der besagt, dass es unendlich viele Primzahlen gibt. Setzt man etwa ${\displaystyle a=N=1}$, so besagt er, dass die Progression

${\displaystyle 1,2,3,4,5,\dots }$

unendlich viele Primzahlen enthält.

Geschichte

Die mathematische Entdeckungsgeschichte über die Verteilung der Primzahlen reicht bis in die Antike zurück. Schon Euklid erkannte, dass es unendlich viele Primzahlen gibt. Sein Resultat wird als der Satz des Euklid bezeichnet. Ab dem 18. Jahrhundert wurde begonnen, dieses qualitative Resultat quantitativ zu vertiefen. Dabei spielten zunehmend Methoden aus der Analysis eine Rolle, die den alten Griechen noch nicht zur Verfügung standen.

Eine Entdeckung Eulers

Leonhard Eulers Entdeckungen zu den Primzahlen waren ein Wegweiser für die kommende Entwicklung von einer elementaren, in der Tradition der alten Griechen stehenden, hin zu einer modernen Form der Zahlentheorie. Im Jahr 1737, während seiner ersten Zeit in Sankt Petersburg, untersuchte Euler einen neuartigen Zugang zu den Primzahlen und fand heraus, dass sie „verhältnismäßig dicht“ unter den natürlichen Zahlen verstreut sind. Genauer bewies er

${\displaystyle (\mathrm {P} )\quad \sum _{p\,{\text{Primzahl}}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .}$

Summiert man also nacheinander die Kehrwerte der Primzahlen, wird auf Dauer jede noch so große obere Schranke durchbrochen. Dies zeigt, dass Primzahlen eher „dicht“ unter den natürlichen Zahlen verstreut sind; zum Beispiel „dichter“ als die Quadratzahlen,^[2] denn ebenfalls Euler zeigte

${\displaystyle 1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}\approx 1{,}645<\infty .}$

Quadratzahlen wachsen also langfristig schnell genug an, dass die Summe ihrer Kehrwerte den endlichen Wert 1,645 nicht überschreitet. Euler stand seiner Zeit nicht die mathematische Sprache zur Verfügung, diese Verschärfung des Euklidischen Satzes präzise zu interpretieren, und es gibt keinen Nachweis, dass er sich mit exakten Aussagen zur Verteilung von Primzahlen beschäftigte.^[3]

Eulers Beweisstrategie für ${\displaystyle (\mathrm {P} )}$ nutzt das sog. Euler-Produkt. Dabei spielt die eindeutige Zerlegbarkeit natürlicher Zahlen in Primfaktoren eine Schlüsselrolle. Das Euler-Produkt steht in Zusammenhang zu einem Objekt, das bis heute in der Primzahlforschung benutzt wird und in der modernen Mathematik als Riemannsche Zeta-Funktion bekannt ist. Die Zeta-Funktion spielt ebenfalls für die Riemannsche Vermutung eine zentrale Rolle. Die neuartige Leistung bestand darin, Fragen zu Primzahlen systematisch durch funktionale Zusammenhänge zwischen Zahlen anzugreifen. Euler gilt deswegen als Initiator der analytischen Zahlentheorie.^[4]

Auch Euler hatte sich bereits Gedanken über Primzahlen in arithmetischen Progressionen gemacht. So behauptete er 1785, dass es zu jeder Zahl ${\displaystyle N}$ unendlich viele Primzahlen mit ${\displaystyle p\equiv 1{\pmod {N}}}$ gibt.^[5]

Erste vollständige Formulierung und Beweisversuche

Zur Gänze wurde das Problem erstmals von Adrien-Marie Legendre im Jahre 1798 formuliert. Dies war verbunden mit dem ersten Beweisversuch, der ebenfalls von Legendre unternommen wurde. In der zweiten Auflage seines Buchs Essai sur la théorie des nombres (publiziert 1808) gab er 1798 einen fehlerhaften Beweis. In der dritten Auflage von 1830 wiederholte er denselben Fehler. Legendres Irrtum verbarg sich hinter den Worten „Wie man einfach sieht, …“, die am Ende des 409. Abschnittes der dritten Auflage auftauchten. Dort skizzierte er den Beweis eines für seinen Beweis zentralen Lemmas, das er in Abschnitt 410 formulierte:

Es seien ${\displaystyle q_{1},\dots ,q_{r}}$ paarweise verschiedene, ungerade Primzahlen, und es bezeichne ${\displaystyle q}$ die ${\displaystyle r}$-te Primzahl, dann gibt es stets innerhalb ${\displaystyle q}$ aufeinanderfolgender Terme in der arithmetischen Progression ${\displaystyle kx+l}$ mit ${\displaystyle \mathrm {ggT} (k,l)=1}$ eine Zahl, die durch keinen der Werte ${\displaystyle q_{j}}$ teilbar ist.

Die Unzulänglichkeit des Beweises von Legendre wurde bereits von Dirichlet hervorgehoben:

Das Lemma von Legendre, das nach A. Desboves (1855) sogar die bis heute unbewiesene Legendre-Vermutung als Konsequenz gehabt hätte, stellte sich schließlich als falsch heraus. Der Fehler wurde zuerst von A. Dupré in einer bei der Paris Academy eingereichten Schrift benannt.^[7] Dupré zeigte, dass es bereits bei ${\displaystyle k=1}$ und mit der Wahl ${\displaystyle q_{j}}$ als die ersten ${\displaystyle r}$ Primzahlen mit ${\displaystyle q_{r}=23,37}$ oder ${\displaystyle 43\leq q_{r}\leq 113}$ scheitert. Dass das Lemma in dieser Konstellation sogar für alle ${\displaystyle q_{r}\geq 43}$ scheitert, wurde 1930 von A. Brauer und H. Zeitz gezeigt.^[7]

Alte Ideen, neuer Zugang: Dirichlet führt Eulers Überlegungen weiter aus

Obwohl Euler das Problem über die Unendlichkeit von Primzahlen in geeigneten arithmetischen Progressionen nicht löste, lieferte er mit der von ihm gezeigten Divergenz der Reihe

${\displaystyle {\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots =\infty }$

über alle Primzahlen bedeutende Vorarbeit. Der erste vollständige Beweis der Vermutung von Legendre wurde von Peter Dirichlet 1837 gegeben, der ihn am 27. Juli desselben Jahres bei einer Konferenz in der Preußischen Akademie der Wissenschaften in Berlin präsentierte. Er gab einen vollständigen Beweis für den Fall mit Primzahlabständen und hatte auch den allgemeinen Fall bis zu einem entscheidenden Punkt entwickelt. Hierfür wurde ein detaillierter Beweis 1839 von Dirichlet nachgeliefert. Dirichlets Beweis zeigte, dass falls ${\displaystyle l_{1},l_{2}}$ zu ${\displaystyle N}$ teilerfremde ganze Zahlen sind, bereits

${\displaystyle \lim _{x\to 1^{+}}{\frac {\sum \limits _{p\ {\text{Primzahl}} \atop p\equiv l_{1}{\pmod {N}}}{\frac {1}{p^{x}}}}{\sum \limits _{p\ {\text{Primzahl}} \atop p\equiv l_{2}{\pmod {N}}}{\frac {1}{p^{x}}}}}=1}$

gelten muss. Dies zeigte zudem, dass die Primzahlen in einem gewissen Sinne gleichverteilt unter den nichttrivialen Restklassen sind. Dies wird mit der, ebenfalls von Dirichlet gezeigten,^[8] Aussage

${\displaystyle \sum _{{p\ {\text{Primzahl}} \atop p\leq x} \atop p\equiv a{\pmod {N}}}{\frac {1}{p}}\sim {\frac {\log(\log(x))}{\varphi (N)}}}$

verdeutlicht, wobei ${\displaystyle \varphi }$ die Eulersche Phi-Funktion bezeichnet. Allerdings waren Dirichlets Methoden nicht geeignet, asymptotische Gleichverteiltheit tatsächlich zu zeigen. Er konnte also nicht

${\displaystyle \lim _{x\to \infty }{\frac {\pi (x;N,l_{1})}{\pi (x;N,l_{2})}}=1}$

beweisen, wobei ${\displaystyle \pi (x;N,l)}$ die Anzahl der Primzahlen ${\displaystyle p\leq x}$ bezeichnet, sodass ${\displaystyle p\equiv l{\pmod {N}}}$ gilt. Ein dafür angefertigter Beweis von Legendre vom Jahr 1830 war fehlerhaft, und der erste korrekte Beweis für die Gleichverteiltheit wurde 1896 unabhängig von Jacques Hadamard und Charles-Jean de La Vallée Poussin erbracht.^[9]

Elementare Beweise für spezielle Moduln

Für gewisse Spezialfälle ist es möglich, einen elementaren Beweis für bestimmte Restklassen zu geben. Diese ähneln dem Beweis des Satzes von Euklid hinsichtlich Mittel und Methodik. Elementar bedeutet, dass nur Sätze aus der elementaren Zahlentheorie angewendet werden, die sämtlich auf Teilbarkeitseigenschaften, wie das Rechnen mit Resten und die Eigenschaft, dass sich jede natürliche Zahl eindeutig als Produkt von Primzahlen zerlegen lässt, aufbauen.

Die Progression 1, 2, 3, 4, …

Bei der Wahl ${\displaystyle a=N=1}$ erhält man die Progression ${\displaystyle 1,2,3,4,\dots }$ In diesem Fall geht der Satz von Dirichlet in den aus der Antike bekannten Satz des Euklid über, der schlicht die Unendlichkeit der Primzahlen beinhaltet. Für den Beweis dieser Aussage kann man für ein beliebiges natürliches ${\displaystyle M}$ die Zahl ${\displaystyle m=M!+1}$ betrachten, wobei ${\displaystyle M!=1\cdot 2\cdots M}$ die Fakultät von ${\displaystyle M}$ bezeichnet. Es ist dann ${\displaystyle m}$ durch keine der Zahlen ${\displaystyle 2,3,4,\dots ,M}$ teilbar. Also gibt es eine Primzahl ${\displaystyle p>M}$. Da ${\displaystyle M}$ beliebig groß gewählt werden kann, folgt die Behauptung.^[10]

Die Fälle 4n+1 und 4n+3

Für einen schnellen Beweis, dass es unendlich viele Primzahlen der Form ${\displaystyle 4n+3}$ gibt, betrachtet man unter der Annahme, dass ${\displaystyle p}$ die größte Primzahl dieser Form ist, das Produkt

${\displaystyle M=2^{2}\cdot 3\cdot 5\cdots p-1.}$

Es wird ausgenutzt, dass die Behauptung folgt, wenn es unendlich viele Primzahlen der Form ${\displaystyle 4n-1}$ gibt (Variablenwechsel ${\displaystyle n\mapsto n-1}$). Das Produkt ${\displaystyle 3\cdot 5\cdots p}$ enthält dabei alle ungeraden Primzahlen ${\displaystyle \leq p}$. Da ${\displaystyle M}$ von der Form ${\displaystyle 4n-1}$ ist, kann es wegen ${\displaystyle M>p}$ nach Annahme keine Primzahl sein. Andererseits übersteigen alle Primfaktoren von ${\displaystyle M}$ die Zahl ${\displaystyle p}$, müssen also von der Form ${\displaystyle 4n+1}$ sein. Da das Produkt zweier, und damit beliebig vieler, Zahlen mit Rest 1 wegen

${\displaystyle (4k+1)(4l+1)=16kl+4k+4l+1=4(4kl+k+l)+1}$

wieder Rest 1 (modulo 4) hat, müsste auch ${\displaystyle M}$ den Rest 1 modulo 4 haben. Allerdings ist ${\displaystyle M}$ von der Form ${\displaystyle 4n-1}$, und dies erzeugt einen Widerspruch.^[11]

Um zu sehen, dass es unendlich viele Primzahlen von der Form ${\displaystyle 4n+1}$ gibt, betrachtet man für eine natürliche Zahl ${\displaystyle M>1}$ den Wert ${\displaystyle m=(M!)^{2}+1}$, wobei ${\displaystyle M!=1\cdot 2\cdots M}$ die Fakultät von ${\displaystyle M}$ bezeichnet. Dann ist ${\displaystyle m}$ offenbar eine ungerade Zahl und größer als 1. Es sei ${\displaystyle p}$ der kleinste Primfaktor von ${\displaystyle m}$. Es teilt nach Konstruktion keine der Zahlen ${\displaystyle 2,\dots ,M}$ den Wert ${\displaystyle m}$, daher muss ${\displaystyle p>M}$ gelten. Offenbar gilt zudem

${\displaystyle (M!)^{2}\equiv -1{\pmod {p}}.}$

Potenziert man beide Seiten mit ${\displaystyle {\tfrac {p-1}{2}}}$ (${\displaystyle p}$ ist ungerade), so findet man

${\displaystyle (M!)^{p-1}\equiv (-1)^{\frac {p-1}{2}}{\pmod {p}}.}$

Nach dem kleinen Satz von Fermat gilt ${\displaystyle (M!)^{p-1}\equiv 1{\pmod {p}}}$, also folgt

${\displaystyle 1\equiv (-1)^{\frac {p-1}{2}}{\pmod {p}}.}$

Da ${\displaystyle p>2}$, sieht man damit schnell, dass ${\displaystyle {\tfrac {p-1}{2}}}$ gerade sein muss, ${\displaystyle p}$ also von der Form ${\displaystyle 4n+1}$ sein muss. Da ${\displaystyle p>M}$ und ${\displaystyle M}$ beliebig groß gewählt war, folgt die Behauptung.^[11]

Die Restklasse 1

Auch für den Fall der Restklasse 1 gibt es elementare Argumente. Zunächst wird dafür gezeigt, dass es unendlich viele Zahlen ${\displaystyle n}$ gibt, sodass eine Primzahl mit ${\displaystyle p\equiv 1{\pmod {n}}}$ existiert.^[12] Ein Beweis dieser Aussage von E. Wendt aus dem Jahre 1895 nutzt dabei die Polynome ${\displaystyle g_{n}(X)}$, die als kleinstes gemeinsames Vielfaches der Polynome ${\displaystyle X^{d}-1}$ mit ${\displaystyle d|n}$ und ${\displaystyle 1\leq d<n}$ definiert sind. Wendt bewies als Zwischenschritt, dass es unendlich viele ganze Zahlen ${\displaystyle x}$ gibt, sodass die Werte ${\displaystyle g_{n}(x)}$ und ${\displaystyle {\tfrac {x^{n}-1}{g_{n}(x)}}}$ teilerfremd sind, was mit elementaren Mitteln gezeigt werden kann.

Nach einer Wahl ${\displaystyle x\in \mathbb {Z} }$ mit ${\displaystyle (f(x),g(x))=1}$ und ${\displaystyle f(x)\notin \{0,\pm 1\}}$ und sei ${\displaystyle q}$ eine Primzahl, die ${\displaystyle f(x)}$ teilt. Es gilt daher ${\displaystyle x^{n}\equiv 1{\pmod {q}}}$. Da ${\displaystyle q\not \mid g(x)}$ folgt, dass für jeden echten Teiler ${\displaystyle d}$ von ${\displaystyle n}$, hat man ${\displaystyle q\not \mid (x^{d}-1)}$. Dies zeigt, dass die Ordnung von ${\displaystyle x{\pmod {q}}}$ genau ${\displaystyle n}$ ist.^[13]

Sätze von Schur und Murty

Die Frage, ob sich für jede Restklasse der Satz von Dirichlet mit einem Argument des „Euklidischen Typs“, also Aufmultiplizieren von Zahlen mit einem abschließenden Widerspruchsargument, beweisen lässt, wurde negativ beantwortet. Issai Schur konnte 1912 zeigen, dass dies in den Fällen von Progressionen ${\displaystyle a,a+N,a+2N,\dots }$ mit ${\displaystyle a^{2}\equiv 1{\pmod {N}}}$ möglich ist.^[14] In all diesen Fällen kann ein Polynom mit ganzzahligen Koeffizienten so generiert werden, dass ein Widerspruch zur Endlichkeit der betroffenen Primzahlen durch eine Euklidische Strategie unter Verwendung des quadratischen Reziprozitätsgesetzes erzeugt werden kann. Etwa hat im Falle der Progression ${\displaystyle 15k+4}$ ein solches Polynom die Gestalt^[15]

${\displaystyle f(x)=x^{4}-x^{3}+2x^{2}+x+1.}$

Dass es zusätzlich in keinem anderen Falle möglich ist als in den von Schur genannten, konnte M. Ram Murty im Jahr 1988 zeigen.^[16]

Analytischer Beweis

Benötigte Grundlagen

Der Satz von Dirichlet wird mit analytischen Mitteln bewiesen. Unumgänglich für ein Verständnis des Beweises ist daher der Begriff der Funktion. Auch eine sichere Beherrschung der aus der Mittelstufe bekannten Potenzgesetze ist unabdingbar.

Rechnen mit Resten

Geht eine ganzzahlige Division nicht auf, kann dies durch die Angabe eines Restes ausgedrückt werden. Etwa ist ${\displaystyle 17}$ geteilt durch ${\displaystyle 4}$ gleich ${\displaystyle 4}$ (Rest ${\displaystyle 1}$). Man sagt auch, dass ${\displaystyle 17}$ kongruent zu ${\displaystyle 1}$ ist, modulo ${\displaystyle 4}$, kurz

${\displaystyle 17\equiv 1{\pmod {4}}.}$

Nach diesem Prinzip lassen sich sämtliche ganze Zahlen durch die Angabe der entsprechenden Restklasse unterteilen. Bleibt man bei der Division durch 4, ergeben sich für ${\displaystyle 0,1,2,3,4,5,6,7,8,\dots }$ die Reste ${\displaystyle 0,1,2,3,0,1,2,3,\dots }$ usw. Es gibt also genau vier Restklassen modulo ${\displaystyle 4}$, und diese sind

${\displaystyle \{0,1,2,3\}.}$

Dies setzt sich auch in die negativen Zahlen fort, etwa hat ${\displaystyle -1}$ bei Division durch ${\displaystyle 4}$ den Rest ${\displaystyle 3}$. Es liegen ${\displaystyle -1,3,7,11}$ usw. alle in derselben Restklasse. Außerdem wird vereinbart, dass ${\displaystyle 0,1,2}$ und ${\displaystyle 3}$ stellvertretend für alle Zahlen stehen, die den jeweiligen Rest besitzen. Es wird also auch ${\displaystyle 12}$ und ${\displaystyle 100}$ mit der ${\displaystyle 0}$ identifiziert, da diese Zahlen ebenfalls restlos durch ${\displaystyle 4}$ teilbar sind. Entfernt man sich nun von der Vorstellung einer Zahl und reduziert das Augenmaß lediglich auf den Rest bei Teilung durch ${\displaystyle 4}$, gilt also ${\displaystyle 0\equiv 12\equiv 100{\pmod {4}}}$, und dies ist die Schreibweise für die Gleichheit von Restklassen.

Man kann mit Restklassen rechnen. Liegen zwei Zahlen ${\displaystyle m}$ und ${\displaystyle n}$ in den Restklassen ${\displaystyle a}$ und ${\displaystyle b}$, so liegt ${\displaystyle m+n}$ in der Klasse zu ${\displaystyle a+b}$. Etwa ist ${\displaystyle 7}$ kongruent ${\displaystyle 3}$ modulo ${\displaystyle 4}$ und ${\displaystyle 5}$ kongruent ${\displaystyle 1}$ modulo ${\displaystyle 4}$, und die Summe ${\displaystyle 7+5=12}$ ist kongruent ${\displaystyle 3+1=4}$ modulo ${\displaystyle 4}$, was aber wieder dem Rest ${\displaystyle 0}$ entspricht. Ähnliches gilt für Produkte von Restklassen. Somit kann gesagt werden, dass Reste „stabil“ unter Addition und Multiplikation sind: So ist es anschaulich gesprochen unerheblich, ob zuerst zwei Zahlen addiert/multipliziert werden, und anschließend mit Rest dividiert wird, oder die bereits ermittelten Einzelreste addiert/multipliziert werden.

Eulersche Phi-Funktion

Die Eulersche Phi-Funktion ordnet einer natürlichen Zahl ${\displaystyle N}$ die Anzahl ${\displaystyle \varphi (N)}$ der Zahlen ${\displaystyle 1\leq k\leq N}$ zu, die teilerfremd zu ${\displaystyle N}$ sind. Dies ist von Bedeutung, weil dies genau der Anzahl an Restklassen ${\displaystyle a}$ entspricht, die gemeinsam mit ${\displaystyle N}$ eine arithmetische Progression liefern, sodass ${\displaystyle a+kN}$ mit ${\displaystyle k\in \mathbb {N} _{0}}$ unendlich viele Primzahlen enthält. Man nennt diese Restklassen auch prim.

Die vier Restklassen modulo ${\displaystyle 4}$ werden durch ${\displaystyle \{0,1,2,3\}}$ repräsentiert. Nur zwei davon, nämlich ${\displaystyle 1}$ und ${\displaystyle 3}$, sind prim, die entsprechenden Repräsentanten also teilerfremd zu ${\displaystyle 4}$, daher gilt ${\displaystyle \varphi (4)=2}$.

Reihen

Unter einer Reihe versteht man, veranschaulicht, eine niemals endende Summe von Zahlen. Dies können reelle, aber auch komplexe Zahlen sein. Die Dezimalschreibweise einer reellen Zahl kann als Reihe aufgefasst werden, etwa

${\displaystyle {\frac {1}{3}}=0{,}333333\ldots =0{,}3+0{,}03+0{,}003+0{,}0003+0{,}00003+0{,}000003+\cdots }$

oder auch

${\displaystyle \pi =3{,}14159\ldots =3+0{,}1+0{,}04+0{,}001+0{,}0005+0{,}00009+\cdots }$

mit der Kreiszahl ${\displaystyle \pi }$. Die durch die Punkte angedeuteten Summen enden niemals, da die Dezimalentwicklung von ${\displaystyle {\tfrac {1}{3}}}$ periodisch und die Kreiszahl irrational ist. Es gibt Reihen, deren Wert nicht als Zahl darstellbar ist,

${\displaystyle 1+2+3+4+\cdots }$

aber auch solche, die gegen einen Grenzwert konvergieren (wie die oberen Beispiele mit Grenzwerten ${\displaystyle {\tfrac {1}{3}}}$ bzw. ${\displaystyle \pi }$). Reihen wie ${\displaystyle 1+2+3+\cdots }$, die nicht konvergieren, nennt man divergent. Veranschaulichend gesagt kann eine Reihe ${\displaystyle \textstyle \sum _{n=1}^{\infty }a_{n}:=a_{1}+a_{2}+a_{3}+\cdots }$ nur dann konvergieren, falls die Glieder ${\displaystyle a_{n}}$ „schnell genug gegen 0 streben“. Aber nicht jede Reihe, deren Glieder gegen 0 streben, konvergiert, wie man an der harmonischen Reihe

${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots =\infty }$

sieht. Eine ganz besondere Form der Konvergenz ist die absolute Konvergenz, bei der gefordert wird, dass die Summe der Absolutbeträge der Reihenglieder konvergiert. In diesem Fall lassen sich auch die Summanden in der Reihe nach Belieben umordnen, ohne den Grenzwert zu verändern.

Dirichlet-Reihen

Es ist auch möglich, Funktionen durch Reihen zu definieren. Ein für den Satz von Dirichlet zentrales Beispiel ist die sog. Riemannsche Zeta-Funktion:

${\displaystyle x\mapsto \zeta (x):=1+{\frac {1}{2^{x}}}+{\frac {1}{3^{x}}}+{\frac {1}{4^{x}}}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{n^{x}}}.}$

Für ${\displaystyle x>1}$ konvergiert diese Reihe immer gegen eine Zahl, die den Funktionswert an der Stelle ${\displaystyle x}$ Darstellt. Damit kann man die Zeta-Funktion auf dem Intervall ${\displaystyle (1,\infty )}$ definieren. Wegen der Divergenz der harmonischen Reihe gilt aber

${\displaystyle \lim _{x\to 1^{+}}\zeta (x)=\infty .}$

Allgemeiner kann man einer Folge von Zahlen ${\displaystyle f(1),f(2),f(3),\dots }$ eine Dirichlet-Reihe zuordnen, via

${\displaystyle D_{f}(x):=f(1)+{\frac {f(2)}{2^{x}}}+{\frac {f(3)}{3^{x}}}+\cdots =\sum _{n=1}^{\infty }{\frac {f(n)}{n^{x}}}.}$

Wächst ${\displaystyle f}$ nicht zu stark an, so gibt es eine Zahl ${\displaystyle x_{0}}$, sodass die Reihe für alle Werte in ${\displaystyle (x_{0},\infty )}$ konvergiert. Für den Fall, dass ${\displaystyle f}$ sogar beschränkt ist, kann stets ${\displaystyle (1,\infty )}$ gewählt werden, da dann wegen ${\displaystyle |f(n)|\leq B}$ und der Konvergenz der Reihe ${\displaystyle B+{\tfrac {B}{2^{x}}}+{\tfrac {B}{3^{x}}}+\cdots =B\zeta (x)}$ für ${\displaystyle x>1}$ erst recht jene über ${\displaystyle f}$ folgt, siehe auch Majorantenkriterium. Dieses Prinzip spielt eine wichtige Rolle beim Beweis des Satzes von Dirichlet.

Euler-Produkte

Der Eckpfeiler zwischen Analysis und Zahlentheorie liegt im Euler-Produkt. Dieses ist eine Identität zwischen einem unendlichen Produkt und einer Reihe und gilt dann, wenn bestimmte Voraussetzungen erfüllt sind.

Haben die Koeffizienten einer Dirichlet-Reihe untereinander eine multiplikative Relation, gilt also ${\displaystyle f(mn)=f(m)f(n)}$ für alle ${\displaystyle m,n}$ ohne gemeinsame Teiler und ferner ${\displaystyle f(1)=1}$, so findet man im Bereich der absoluten Konvergenz der Dirichlet-Reihe

${\displaystyle \prod _{p\ {\text{Primzahl}}}\left(\sum _{m=0}^{\infty }{\frac {f(p^{m})}{p^{mx}}}\right)=\left(1+{\frac {f(2)}{2^{x}}}+{\frac {f(2^{2})}{4^{x}}}+{\frac {f(2^{3})}{8^{x}}}+\cdots \right)\cdot \left(1+{\frac {f(3)}{3^{x}}}+{\frac {f(3^{2})}{9^{x}}}+{\frac {f(3^{3})}{27^{x}}}+\cdots \right)\cdot \left(1+{\frac {f(5)}{5^{x}}}+\cdots \right)\cdot \left(1+{\frac {f(7)}{7^{x}}}+\cdots \right)\cdots }$

${\displaystyle =1+{\frac {f(2)}{2^{x}}}+{\frac {f(3)}{3^{x}}}+{\frac {f(4)}{4^{x}}}+{\frac {f(5)}{5^{x}}}+\cdots =\sum _{n=1}^{\infty }{\frac {f(n)}{n^{x}}}.}$

Die Formel lässt sich mittels des Prinzips, dass sich jede Zahl eindeutig als Produkt von Primzahlpotenzen schreiben lässt, und gewöhnliches Ausmultiplizieren von Klammern, erklären. Etwa ergibt sich für den Faktor ${\displaystyle {\tfrac {f(1092)}{1092^{x}}}}$ auf der rechten Seite wegen ${\displaystyle 1092=2^{2}\cdot 3\cdot 7\cdot 13}$:

${\displaystyle {\frac {f(1092)}{1092^{x}}}={\frac {f(2^{2}\cdot 3\cdot 7\cdot 13)}{(2^{2}\cdot 3\cdot 7\cdot 13)^{x}}}={\frac {f(2^{2})}{2^{2x}}}\cdot {\frac {f(3)}{3^{x}}}\cdot {\frac {f(7)}{7^{x}}}\cdot {\frac {f(13)}{13^{x}}}.}$

Dabei wurde die von ${\displaystyle f}$ geforderte Multiplikativität ausgenutzt – es sind naturgemäß Potenzen verschiedener Primzahlen ohne gemeinsame (nichttriviale) Teiler. Der Term zur Linken kann nun durch die entsprechende Auswahl an Summanden in den Klammern beim Ausmultiplizieren gewonnen werden.

Eine noch stärkere Version des Euler-Produktes erhält man, wenn die Koeffizienten sogar vollständig multiplikativ sind, also ${\displaystyle f(mn)=f(m)f(n)}$ für ausnahmslos alle natürlichen Zahlen ${\displaystyle n,m}$ erfüllt ist und erneut ${\displaystyle f(1)=1}$ gilt. Dann gilt insbesondere ${\displaystyle f(p^{m})=f(p)^{m}}$ für alle Primzahlen ${\displaystyle p}$, und man erhält mit der geometrischen Reihe:^[17]

${\displaystyle (\mathrm {E} )\quad D_{f}(x)=\prod _{p\ {\text{Primzahl}}}\left(\sum _{m=0}^{\infty }{\frac {f(p^{m})}{p^{mx}}}\right)=\prod _{p\ {\text{Primzahl}}}\left(\sum _{m=0}^{\infty }{\frac {f(p)^{m}}{p^{mx}}}\right)=\prod _{p\ {\text{Primzahl}}}{\frac {1}{1-{\frac {f(p)}{p^{x}}}}}.}$

Logarithmen

Von entscheidender Bedeutung für den Beweis sind Logarithmen. Mit diesen wird ermöglicht, das Euler-Produkt (mit Primzahlfaktoren) auf eine Summe mit Primzahltermen zurückzuführen. Dabei wird die für Logarithmen eigentümliche Beziehung

${\displaystyle \log(ab)=\log(a)+\log(b)}$

mit ${\displaystyle a,b>0}$ ausgenutzt, die sich unter gewissen Bedingungen aber auch auf komplexe Zahlen ausdehnt. Man erhält für vollständig multiplikative ${\displaystyle f}$ zusammen mit ${\displaystyle (\mathrm {E} )}$ im absoluten Konvergenzbereich:

${\displaystyle (\mathrm {L} _{0})\quad \log(D_{f}(x))=\sum _{p\ {\text{Primzahl}}}\log \left({\frac {1}{1-{\frac {f(p)}{p^{x}}}}}\right).}$

Es wird stets der natürliche Logarithmus betrachtet, also jener zur Basis ${\displaystyle e}$ (Eulersche Zahl), weil dieser eine besonders einfache Ableitung besitzt, nämlich

${\displaystyle \log '(w)={\frac {1}{w}}.}$

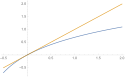
Wegen ${\displaystyle \log(1)=0}$ und ${\displaystyle \log '(1)={\tfrac {1}{1}}=1}$ ist die Ursprungsgerade für kleine Werte ${\displaystyle w}$ eine sehr gute Annäherung an ${\displaystyle w\mapsto \log(1+w)}$, siehe Bild. Der Fehler ist hierbei quadratisch, es gilt also

${\displaystyle \log(1+w)=w+O(w^{2}),\qquad w\to 0}$

in Termen der Landau-O-Notation. Diese Annäherung, die erst durch die Differentialrechnung ermöglicht wird, ist von großer Bedeutung, da sie hilft, die auftretenden Logarithmen durch deutlich leichtere lineare Funktionen zu ersetzen, wobei der Fehler vernachlässigt werden kann. Zusammen mit ${\displaystyle \log({\tfrac {1}{w}})=-\log(w)}$ erhält man mit ${\displaystyle (\mathrm {E} )}$ und ${\displaystyle (\mathrm {L} _{0})}$ für ${\displaystyle x\to 1^{+}}$

${\displaystyle (\mathrm {L} )\quad \log(D_{f}(x))=\sum _{p\ {\text{Primzahl}}}{\frac {f(p)}{p^{x}}}+O(1).}$

Dabei steht die Abkürzung ${\displaystyle O(1)}$ für eine Funktion, deren Werte ${\displaystyle x\geq 1}$ für ${\displaystyle x\to 1^{+}}$ beschränkt sind.

Eine erste Anwendung dieses Prinzips umfasst einen Beweis von ${\displaystyle (\mathrm {P} )}$. Da die Funktion ${\displaystyle f(n)=1}$ offenbar stark multiplikativ ist, da Produkte von Einsen immer Einsen sind, gilt mit ${\displaystyle (\mathrm {L} )}$

${\displaystyle \log \left(1+{\frac {1}{2^{x}}}+{\frac {1}{3^{x}}}+\cdots \right)=\log(\zeta (x))=\sum _{p\ {\text{Primzahl}}}{\frac {1}{p^{x}}}+O(1).}$

Da die harmonische Reihe divergiert und auch Logarithmen unbeschränkt anwachsen, gilt ${\displaystyle \lim _{x\to 1^{+}}\log(\zeta (x))=\infty }$, also ist auch die rechte Primzahlreihe für ${\displaystyle x\to 1^{+}}$ unbeschränkt, da der beschränkte Term ${\displaystyle O(1)}$ das durch die Gleichheit gegebene Wachstum nicht gewährleisten kann.^[18]

Erläuterung der Strategie an einem Beispiel

Die Erläuterung der Beweisstrategie von Dirichlet wird mit einem Beispielfall begleitet. Es wird der Fall ${\displaystyle a=3}$ und ${\displaystyle N=4}$ betrachtet, d. h., es wird exemplarisch gezeigt, dass die Progression

${\displaystyle 3,7,11,15,19,23,27,31,35,\dots }$

unendlich viele Primzahlen

${\displaystyle 3,7,11,19,23,31,\dots }$

enthält. Es wird sogar noch eine stärkere Aussage gezeigt: Dirichlet konnte nachweisen, dass die Summe über alle Kehrwerte der Primzahlen ${\displaystyle p\equiv 3{\pmod {4}}}$ divergiert, also ${\displaystyle {\tfrac {1}{3}}+{\tfrac {1}{7}}+{\tfrac {1}{11}}+{\tfrac {1}{19}}+{\tfrac {1}{23}}+\cdots =\infty .}$ Definiert man auf den ganzen Zahlen eine Funktion ${\displaystyle f_{4,3}}$, die nur an den „passenden“ Zahlen ${\displaystyle \dots ,-1,3,7,11,15,19,23,\dots }$ den Wert ${\displaystyle 1}$ annimmt, und sonst nur ${\displaystyle 0}$, so kann man die zu untersuchende Reihe auch als Reihe über alle Primzahlen schreiben:

${\displaystyle {\frac {1}{3}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{19}}+{\frac {1}{23}}+\cdots =\sum _{p\ {\text{Primzahl}}}{\frac {f_{4,3}(p)}{p}}.}$

Die Strategie sieht vor, die Divergenz der Eulerschen Primzahlreihe ${\displaystyle (\mathrm {P} )}$ zu nutzen, um daraus die Divergenz der oberen Primzahlreihe zu erzwingen. Dafür führt man die Variable ${\displaystyle x\geq 1}$ ein, und beweist

${\displaystyle (*)\quad \lim _{x\to 1^{+}}\sum _{p\ {\text{Primzahl}}}{\frac {f_{4,3}(p)}{p^{x}}}=\infty .}$

Die Schlüsselidee ist, geeignete Abbildungen ${\displaystyle \chi _{0}}$ und ${\displaystyle \chi _{1}}$ auf den Restklassen ${\displaystyle \{0,1,2,3\}}$ zu definieren. Diese erweitern sich durch 4-Periodizität auf Abbildungen auf den ganzen Zahlen und sollen die folgende Eigenschaften haben:

1. Ausschluss der trivialen Restklassen: Es nehmen beide Funktionen auf ${\displaystyle 0}$ und ${\displaystyle 2}$ den Wert ${\displaystyle 0}$ an.
2. Möglichkeit, nur Primzahlen in der passenden Restklasse zu betrachten: Es lässt sich jede ${\displaystyle 4}$-periodische Funktion auf ${\displaystyle 1}$ und ${\displaystyle 3}$, also insgesamt den Zahlen ${\displaystyle \dots ,-3,-1,1,3,5,\dots }$, durch ${\displaystyle \chi _{0}}$ und ${\displaystyle \chi _{1}}$ durch geeignete Linearkombination erzeugen.
3. Multiplikativität bzw. Euler-Produkt Eigenschaft: Es gilt ${\displaystyle \chi _{j}(mn)=\chi _{j}(m)\chi _{j}(n)}$ für alle ${\displaystyle m,n}$ und ${\displaystyle j=0,1}$, also sind die Erzeuger ${\displaystyle \chi _{0}}$ und ${\displaystyle \chi _{1}}$ vollständig multiplikativ.

Durch die oberen Bedingungen lassen sich tatsächlich genau zwei solche Funktionen finden:^[19]

Da die Vektoren ${\displaystyle {\binom {1}{1}}}$ und ${\displaystyle {\binom {1}{-1}}}$ linear unabhängig sind, gilt Eigenschaft 2, und man kann aus diesen beiden Funktionen jede 4-periodische Funktion auf den ganzen Zahlen kombinieren, die auf geraden Zahlen verschwindet. Von Interesse ist die Abbildung ${\displaystyle f_{4,3}(4k+3)=1}$ für alle ${\displaystyle k\in \mathbb {Z} }$, und ${\displaystyle f_{4,3}(n)=0}$ sonst, da man sich im Beispiel nur für Primzahlen in der Progression ${\displaystyle (4k+3)_{k\in \mathbb {N} _{0}}}$ interessiert. Es gilt ${\displaystyle f_{4,3}(n)={\tfrac {\chi _{0}(n)-\chi _{1}(n)}{2}}}$. Also gilt

${\displaystyle {\frac {1}{3^{x}}}+{\frac {1}{7^{x}}}+{\frac {1}{11^{x}}}+{\frac {1}{19^{x}}}+{\frac {1}{23^{x}}}+\cdots =\sum _{p\ {\text{Primzahl}}}{\frac {f_{4,3}(p)}{p^{x}}}={\frac {1}{2}}\sum _{p\ {\text{Primzahl}}}{\frac {\chi _{0}(p)}{p^{x}}}-{\frac {1}{2}}\sum _{p\ {\text{Primzahl}}}{\frac {\chi _{1}(p)}{p^{x}}}.}$

Offensichtlich gilt nach Euler ${\displaystyle (\mathrm {P} )}$

${\displaystyle \lim _{x\to 1^{+}}{\frac {1}{2}}\sum _{p\ {\text{Primzahl}}}{\frac {\chi _{0}(p)}{p^{x}}}=\infty ,}$

da stets ${\displaystyle \chi _{0}(p)=1}$ für alle ${\displaystyle p>2}$ ist, und der einzig fehlende Summand für ${\displaystyle p=2}$ natürlich nichts an der Divergenz ändert. Kann man außerdem zeigen, dass die Funktion

${\displaystyle x\mapsto {\frac {1}{2}}\sum _{p\ {\text{Primzahl}}}{\frac {\chi _{1}(p)}{p^{x}}}}$

für ${\displaystyle x\to 1^{+}}$ beschränkt ist, folgt insgesamt ${\displaystyle (*)}$. Es ist ${\displaystyle \chi _{1}}$ vollständig multiplikativ, also folgt mit ${\displaystyle (\mathrm {L} )}$ für ${\displaystyle x\to 1^{+}}$:

${\displaystyle \log \left(1-{\frac {1}{3^{x}}}+{\frac {1}{5^{x}}}-{\frac {1}{7^{x}}}+\cdots \right)=\sum _{p\ {\text{Primzahl}}}{\frac {\chi _{1}(p)}{p^{x}}}+O(1).}$

Es ist aber auch

${\displaystyle \lim _{x\to 1^{+}}\log \left(1-{\frac {1}{3^{x}}}+{\frac {1}{5^{x}}}-{\frac {1}{7^{x}}}+\cdots \right)=\log \left(1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots \right)<\infty ,}$

da die alternierende Reihe ${\displaystyle 1-{\tfrac {1}{3}}+{\tfrac {1}{5}}-{\tfrac {1}{7}}+\cdots }$ gegen eine positive Zahl konvergiert nach dem Leibniz-Kriterium.^{[Anm. 1]} Es muss also ${\displaystyle \textstyle {\tfrac {1}{2}}\sum \limits _{p\ {\text{Primzahl}}}{\tfrac {\chi _{1}(p)}{p^{x}}}}$ für ${\displaystyle x\to 1^{+}}$ beschränkt sein.^[20][21]

Der allgemeine Fall

Im allgemeinen Fall ist es von entscheidender Bedeutung, Funktionen ${\displaystyle \chi _{0},\chi _{1},\dots ,\chi _{\varphi (N)-1}}$ auf den nichttrivialen Restklassen modulo ${\displaystyle N}$ zu finden, die dort sämtliche Kombinationsfreiheit lassen und darüber hinaus vollständig multiplikativ sind. Dass dies immer möglich ist, ist nicht trivial. Solche Funktionen bezeichnet man auch als Dirichlet-Charaktere.^[22] Es gibt im Allgemeinen ${\displaystyle \varphi (N)}$ verschiedene sog. prime Restklassen ${\displaystyle l{\pmod {N}}}$, sodass also ${\displaystyle l}$ und ${\displaystyle N}$ teilerfremd sind. Im obigen Spezialfall hatte man ${\displaystyle \varphi (4)=2}$, denn ${\displaystyle 1}$ und ${\displaystyle 3}$ sind teilerfremd zu ${\displaystyle 4}$, nicht aber ${\displaystyle 0}$ und ${\displaystyle 2}$.

Einem beliebigen Dirichlet-Charakter ${\displaystyle \chi }$ kann eine Dirichlet-Reihe zugeordnet werden:

${\displaystyle L(s;\chi ):=\sum _{n=1}^{\infty }{\frac {\chi (n)}{n^{s}}}.}$

Diese wird auch als Dirichletsche L-Funktion zu ${\displaystyle \chi }$ bezeichnet. Es gilt für komplexe Zahlen ${\displaystyle s}$ mit ${\displaystyle \mathrm {Re} (s)>1}$^[23]

${\displaystyle L(s;\chi )=\prod _{p\ {\text{Primzahl}}}{\frac {1}{1-{\frac {\chi (p)}{p^{s}}}}}.}$

Der Charakter, der auf allen Restklassen ${\displaystyle a}$ mit ${\displaystyle \mathrm {ggT} (a,N)=1}$ den Wert 1 annimmt (und ansonsten 0), heißt auch Hauptcharakter. Dieser korrespondiert zur Reihe von Euler über die Kehrwerte der Primzahlen, die bekanntermaßen divergiert. Alle anderen Charaktere nehmen auch Werte außer 0 und 1 an, im allgemeinen Fall komplexe Einheitswurzeln. Die oben demonstrierte Beweisidee ist im Allgemeinen die Gleiche. Als Ausgangspunkt wird die aus den Orthogonalitätsrelationen gewinnbare Identität^[24]

${\displaystyle \sum _{p\ {\text{Primzahl}} \atop p\ \equiv a\ {\pmod {N}}}{\frac {1}{p^{x}}}={\frac {1}{\varphi (N)}}\sum _{\chi \ {\pmod {N}}}{\overline {\chi (a)}}\sum _{p\ {\text{Primzahl}}}{\frac {\chi (p)}{p^{x}}}={\frac {1}{\varphi (N)}}\sum _{p\ {\text{Primzahl}} \atop \mathrm {ggT} (p,N)=1}{\frac {1}{p^{x}}}+{\frac {1}{\varphi (N)}}\sum _{\chi \not =\chi _{0}\ {\pmod {N}}}{\overline {\chi (a)}}\sum _{p\ {\text{Primzahl}}}{\frac {\chi (p)}{p^{x}}}}$

genutzt. Wie im obigen Beispiel wird die benötigte Funktion, die nur für die interessanten Primzahlen den Wert ${\displaystyle 1}$ annimmt, und sonst nur ${\displaystyle 0}$, durch Dirichlet-Charaktere linear kombiniert. Die hinteren Summen ${\displaystyle \textstyle \sum \limits _{p\ {\text{Primzahl}}}{\frac {\chi (p)}{p^{x}}}}$ verhalten sich für ${\displaystyle x\to 1^{+}}$ wegen des Euler-Produktes, bzw. ${\displaystyle (\mathrm {L} )}$, im Wesentlichen wie ${\displaystyle \log(L(x;\chi ))}$. Dabei ist ${\displaystyle {\overline {\chi (a)}}}$ das komplex Konjugierte von ${\displaystyle \chi (a)}$. Die äußere Summe läuft dabei über alle Charaktere modulo ${\displaystyle N}$. Da nur endlich viele Primzahlen ${\displaystyle p}$ auch ${\displaystyle \mathrm {ggT} (p,N)\not =1}$ erfüllen, folgt mit Eulers Resultat ${\displaystyle (\mathrm {P} )}$