Dehn-Twist

In der Topologie, einem Teilgebiet der Mathematik, sind Dehn-Twists bestimmte Selbstabbildungen von Flächen. Dehn-Twists wurden von Max Dehn eingeführt, der sie ursprünglich als "Schraubungen" bezeichnete.^[1]

Definition

Sei ${\displaystyle S}$ eine orientierbare Fläche und ${\displaystyle c\subset S}$ eine einfache geschlossene Kurve. Sei ${\displaystyle U}$ eine Tubenumgebung von ${\displaystyle c}$, das heißt, wir haben einen Homöomorphismus ${\displaystyle U\cong S^{1}\times \left[0,1\right]}$, der ${\displaystyle c}$ auf ${\displaystyle S^{1}\times \left\{1/2\right\}}$ abbildet. Wir benutzen diesen Homöomorphismus, um ${\displaystyle U}$ durch Koordinaten ${\displaystyle (e^{i\theta },t)}$ mit ${\displaystyle \theta \in \left[0,2\pi \right),t\in \left[0,1\right]}$ zu parametrisieren.

Wir definieren dann eine Abbildung ${\displaystyle t_{c}:U\rightarrow U}$ durch

${\displaystyle t_{c}(e^{i\theta },t)=(e^{i(\theta +2\pi t)},t)}$.

Weil ${\displaystyle t_{c}}$ auf ${\displaystyle \partial U\cong S^{1}\times \left\{0,1\right\}}$ mit der Identität übereinstimmt, können wir es auf ${\displaystyle S\setminus U}$ durch die Identitätsabbildung stetig fortsetzen und erhalten so einen Homöomorphismus ${\displaystyle t_{c}:S\rightarrow S}$, der als Dehn-Twist an der Kurve c bezeichnet wird.

Anmerkung: Die oben definierte Abbildung ${\displaystyle t_{c}:S\rightarrow S}$ hängt von der gewählten Umgebung und der gewählten Parametrisierung ab. Für andere Umgebungen und andere Parametrisierungen bekommt man mit dieser Konstruktion aber zueinander homotope Abbildungen. Die Homotopieklasse (Abbildungsklasse) von ${\displaystyle t_{c}}$ ist also wohldefiniert.

Beispiele

Longitude und Meridian des Torus.

Wir identifizieren den Torus mit ${\displaystyle \mathbb {R} ^{2}/\mathbb {Z} ^{2}}$. Jede Matrix aus ${\displaystyle SL(2,\mathbb {Z} )}$ entspricht dann einer Selbstabbildung des Torus. (Die Matrix wirkt linear auf ${\displaystyle \mathbb {R} ^{2}}$ und bildet ${\displaystyle \mathbb {Z} ^{2}}$ nach ${\displaystyle \mathbb {Z} ^{2}}$ ab. Man kann zeigen, dass jeder orientierungserhaltende Homöomorphismus des Torus homotop zu einer solchen Abbildung ist.)

Die Matrizen ${\displaystyle \left({\begin{array}{cc}1&1\\0&1\end{array}}\right)}$ und ${\displaystyle \left({\begin{array}{cc}1&0\\1&1\end{array}}\right)}$ entsprechen dann den Dehn-Twists an Longitude und Meridian (also an den Bildern der x- und y-Achse.)

Abbildungsklassengruppe

Die Dehn-Twists an diesen 3g-1 Kurven (hier für g=3) erzeugen die Abbildungsklassengruppe.

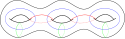
Sei ${\displaystyle S_{g}}$ die geschlossene, orientierbare Fläche vom Geschlecht ${\displaystyle g}$ und ${\displaystyle MCG(S_{g})}$ ihre Abbildungsklassengruppe. Für ${\displaystyle g=1}$ (den Torus) ist ${\displaystyle MCG(S_{1})\cong SL(2,\mathbb {Z} )}$ und man kann mit Hilfe des Euklidischen Algorithmus beweisen, dass ${\displaystyle SL(2,\mathbb {Z} )}$ von den Matrizen ${\displaystyle \left({\begin{array}{cc}1&1\\0&1\end{array}}\right)}$ und ${\displaystyle \left({\begin{array}{cc}1&0\\1&1\end{array}}\right)}$ erzeugt wird, also von den Dehn-Twists an Longitude und Meridian. Max Dehn bewies auch für alle ${\displaystyle g\geq 2}$, dass die Abbildungsklassengruppe ${\displaystyle MCG(S_{g})}$ von Dehn-Twists erzeugt wird. Lickorish zeigte, dass die im Bild rechts dargestellten ${\displaystyle 3g-1}$ Dehn-Twists die Abbildungsklassengruppe erzeugen. Humphries bewies, dass für ${\displaystyle g\geq 2}$ die Abbildungsklassengruppe von ${\displaystyle 2g+1}$ Dehn-Twists erzeugt wird und dass dies die kleinstmögliche Zahl von Erzeugern ist.

Verallgemeinerte Dehn-Twists

Sei ${\displaystyle M}$ eine symplektische Mannigfaltigkeit und ${\displaystyle V\subset M}$ eine Lagrangesche Sphäre. Nach einem Satz von Weinstein gibt es eine Umgebung ${\displaystyle U\subset M}$ von ${\displaystyle V}$, die symplektomorph zu einer Umgebung von ${\displaystyle S^{n}}$ im Kotangentialbündel ${\displaystyle T^{*}S^{n}=\left\{(u,v)\in \mathbb {R} ^{n+1}\times \mathbb {R} ^{n+1}\colon |u|=1,\langle u,v\rangle =0\right\}}$ (mit der kanonischen symplektischen Struktur ${\displaystyle \textstyle \sum _{j=1}^{n+1}du_{j}dv_{j}}$) ist. Es genügt deshalb, verallgemeinerte Dehn-Twists für Umgebungen von ${\displaystyle S^{n}}$ in ${\displaystyle T^{*}S^{n}}$ zu definieren.

Die Funktion ${\displaystyle \mu (u,v)=|v|}$ ist glatt außerhalb des Null-Schnittes, ihr Hamiltonscher Fluss ${\displaystyle \phi _{t}^{\mu }}$ ist der normalisierte geodätische Fluss. Die Abbildung ${\displaystyle \phi _{\pi }^{\mu }}$ lässt sich auf den Null-Schnitt fortsetzen, weil alle Geodäten der Länge ${\displaystyle \pi }$ denselben Endpunkt haben. Die so definierte Abbildung ${\displaystyle \tau _{V}:M\rightarrow M}$ ist ein Symplektomorphismus und man kann sie so modifizieren, dass sie außerhalb einer kompakten Umgebung die Identität ist.^[2] Für ${\displaystyle n\geq 2}$ ist ${\displaystyle \tau _{V}^{2}}$ homotop zur Identität, während für ${\displaystyle n=1}$ (also für Dehn-Twists auf Flächen) die Dehn-Twists unendliche Ordnung in der Abbildungsklassengruppe haben.

Belege

1. ↑ M. Dehn: Die Gruppe der Abbildungsklassen. Das arithmetische Feld auf Flächen. In: Acta Math. 69, no. 1, 1938, S. 135–206.
2. ↑ P. Seidel: Floer homology and the symplectic isotopy problem. Oxford 1997. (www-math.mit.edu; pdf)

Weblinks

Video zur Veranschaulichung von Dehn-Twists auf dem Torus

Literatur

• Benson Farb, Dan Margalit: A primer on mapping class groups. (= Princeton Mathematical Series. 49). Princeton University Press, Princeton, NJ, 2012, ISBN 978-0-691-14794-9.