Chi-Quadrat-Verteilung

Die Chi-Quadrat-Verteilung bzw. ${\displaystyle \chi ^{2}}$-Verteilung (ältere Bezeichnung: Helmert-Pearson-Verteilung, nach Friedrich Robert Helmert und Karl Pearson) ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der nichtnegativen reellen Zahlen. Üblicherweise ist mit „Chi-Quadrat-Verteilung“ die zentrale Chi-Quadrat-Verteilung gemeint. Die Chi-Quadrat-Verteilung hat einen einzigen Parameter, nämlich die Anzahl der Freiheitsgrade ${\displaystyle n}$.

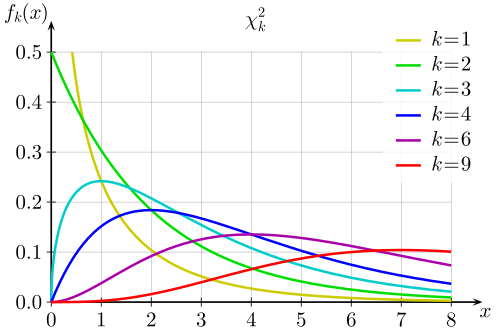
Sie ist eine der Verteilungen, die aus der Normalverteilung ${\displaystyle {\mathcal {N}}\left(\mu ,\sigma ^{2}\right)}$ abgeleitet werden kann: Sind ${\displaystyle Z_{1},...,Z_{n}}$ unabhängige und standardnormalverteilte Zufallsvariablen, so ist die Chi-Quadrat-Verteilung mit ${\displaystyle n}$ Freiheitsgraden definiert als die Verteilung der Summe ${\displaystyle Z_{1}^{2}+\dotsb +Z_{n}^{2}}$ der quadrierten Zufallsvariablen. Solche Summen quadrierter Zufallsvariablen treten bei Schätzfunktionen wie der Stichprobenvarianz zur Schätzung der empirischen Varianz auf. Die Chi-Quadrat-Verteilung ermöglicht damit unter anderem ein Urteil über die Kompatibilität eines vermuteten funktionalen Zusammenhangs (Abhängigkeit von der Zeit, Temperatur, Druck etc.) mit empirisch ermittelten Messpunkten. Kann z. B. eine Gerade die Daten erklären, oder braucht man doch eine Parabel oder vielleicht einen Logarithmus? Man wählt verschiedene Modelle aus, und dasjenige mit der besten Anpassungsgüte, dem kleinsten Chi-Quadrat-Wert, bietet die beste Erklärung der Daten.^[1][2] So stellt die Chi-Quadrat-Verteilung durch die Quantifizierung der zufälligen Schwankungen die Auswahl verschiedener Erklärungsmodelle auf eine numerische Basis. Außerdem erlaubt sie, wenn man die empirische Varianz bestimmt hat, die Schätzung des Vertrauensintervalls, das den (unbekannten) Wert der Varianz der Grundgesamtheit mit einer gewissen Wahrscheinlichkeit einschließt. Diese und weitere Anwendungen sind weiter unten und im Artikel Chi-Quadrat-Test beschrieben.

Die Chi-Quadrat-Verteilung wurde 1876 eingeführt von Friedrich Robert Helmert, die Bezeichnung stammt von Karl Pearson (1900).^[3]

Sind ${\displaystyle Z_{1},\dotsc ,Z_{n}}$stochastisch unabhängige und standardnormalverteilte Zufallsvariablen, so heißt die Verteilung der Zufallsvariablen ${\displaystyle X}$ mit

${\displaystyle X=Z_{1}^{2}+\cdots +Z_{n}^{2}}$

Chi-Quadrat-Verteilung mit ${\displaystyle n}$ Freiheitsgraden.^[4] Hierfür schreibt man symbolisch

${\displaystyle X\sim \chi _{n}^{2}\quad {\text{oder}}\quad X\sim \chi ^{2}(n)}$

und sagt, dass sie ${\displaystyle \chi _{n}^{2}}$-verteilt ist.

Hinweis: In der Statistik werden oftmals Stichprobenfunktionen, die unter gewissen Bedingungen chi-Quadrat-verteilt sind, mit ${\displaystyle \chi ^{2}}$ bezeichnet.

Die Summe quadrierter Größen kann keine negativen Werte annehmen. Deshalb hat die Dichte ${\displaystyle f_{n}}$ der ${\displaystyle \chi _{n}^{2}}$-Verteilung für ${\displaystyle x<0}$ den Wert null. Für ${\displaystyle x>0}$ lässt sie sich darstellen als

${\displaystyle f_{n}(x)={\frac {1}{2^{\frac {n}{2}}\Gamma ({\tfrac {n}{2}})}}x^{{\frac {n}{2}}-1}\exp \left(-{\frac {x}{2}}\right).}$^[4]

Dabei steht ${\displaystyle \Gamma }$ für die Gammafunktion. Die Werte von ${\displaystyle \Gamma ({\tfrac {n}{2}})}$ kann man rekursiv aus

${\displaystyle \Gamma ({\tfrac {1}{2}})={\sqrt {\pi }}\;,\quad \Gamma (1)=1\;,}$

${\displaystyle \Gamma (x+1)=x\cdot \Gamma (x)\quad {\text{mit}}\quad x\in \mathbb {R} ^{+}}$

berechnen.

Spezialfall: Für die Dichte ${\displaystyle f_{2}}$ der ${\displaystyle \chi ^{2}}$-Verteilung mit ${\displaystyle n=2}$ Freiheitsgraden gilt für ${\displaystyle x>0}$

${\displaystyle f_{2}(x)={\frac {1}{2}}\exp \left(-{\frac {x}{2}}\right).}$

Die Verteilungsfunktion kann man mit Hilfe der regularisierten unvollständigen Gammafunktion ${\displaystyle P(a,x)}$ ausdrücken:

${\displaystyle F_{n}(x)=P({\tfrac {n}{2}},{\tfrac {x}{2}}).}$

Wenn ${\displaystyle n}$ eine natürliche Zahl ist, dann kann die Verteilungsfunktion wie folgt dargestellt werden:

${\displaystyle P\left({\tfrac {n}{2}},{\tfrac {x}{2}}\right)={\begin{cases}1-e^{-{\frac {x}{2}}}\sum \limits _{k=0}^{n/2-1}{\frac {1}{\Gamma (k+1)}}({\tfrac {x}{2}})^{k}&{\text{ falls }}n{\text{ gerade}},\\\operatorname {erf} \left({\sqrt {\tfrac {x}{2}}}\right)-e^{-{\frac {x}{2}}}\sum \limits _{k=0}^{\lfloor n/2\rfloor -1}{\frac {1}{\Gamma (k+{\tfrac {3}{2}})}}({\tfrac {x}{2}})^{k+{\tfrac {1}{2}}}&{\text{ falls }}n{\text{ ungerade}},\end{cases}}}$

wobei ${\displaystyle \operatorname {erf} }$ die Fehlerfunktion bezeichnet.

Spezialfall: Für die Verteilungsfunktion ${\displaystyle F_{2}}$ der ${\displaystyle \chi ^{2}}$-Verteilung mit ${\displaystyle n=2}$ Freiheitsgraden gilt für ${\displaystyle x>0}$

${\displaystyle F_{2}(x)=1-\exp \left(-{\frac {x}{2}}\right).}$

Ist ${\displaystyle X}$ die Summe der Quadrate von ${\displaystyle m}$ unabhängigen standardnormalverteilten Zufallsvariablen und ${\displaystyle Y}$ die Summe der Quadrate von ${\displaystyle n}$ unabhängigen standardnormalverteilten Zufallsvariablen, so gilt

${\displaystyle X\sim \chi _{m}^{2}}$ und ${\displaystyle Y\sim \chi _{n}^{2}}$.

Die Summe ${\displaystyle X+Y}$ ist dann aber die Summe der Quadrate von ${\displaystyle m+n}$ unabhängigen standardnormalverteilten Zufallsvariablen, also gilt

${\displaystyle X+Y\sim \chi _{m+n}^{2}}$.

Die Chi-Quadrat-Verteilung ist also reproduktiv.

Der Erwartungswert einer chi-quadrat-verteilten Zufallsvariable mit ${\displaystyle n}$ Freiheitsgraden ist

${\displaystyle \operatorname {E} \left(\chi _{n}^{2}\right)=n}$.

Die Varianz einer chi-quadrat-verteilten Zufallsvariable mit ${\displaystyle n}$ Freiheitsgraden beträgt

${\displaystyle \operatorname {Var} (\chi _{n}^{2})=2n}$.

Eine Chi-Quadrat-Verteilung mit ${\displaystyle n\geq 3}$ Freiheitsgraden hat den Modus ${\displaystyle n-2}$. Die Dichte der Chi-Quadrat-Verteilungen mit einem und zwei Freiheitsgraden nimmt das Supremum auf dem offenen Intervall ${\displaystyle (0,\infty )}$ nicht an, die Dichten sind in diesen beiden Fällen aber monoton fallend. Man findet daher auch teils die Bezeichnung Modus 0 für die Chi-Quadrat-Verteilungen mit einem und zwei Freiheitsgraden.

Die Schiefe ${\displaystyle \gamma _{m}}$ der Chi-Quadrat-Verteilung mit ${\displaystyle n}$ Freiheitsgraden ist

${\displaystyle \gamma _{m}(\chi _{n}^{2})={\frac {2{\sqrt {2}}}{\sqrt {n}}}}$.

Die Chi-Quadrat-Verteilung besitzt eine positive Schiefe, d. h., sie ist linkssteil- bzw. rechtsschief. Je höher die Anzahl der Freiheitsgrade ${\displaystyle n}$, desto weniger schief ist die Verteilung.

Die Kurtosis (Wölbung) ${\displaystyle \beta _{2}}$ der Chi-Quadrat-Verteilung mit ${\displaystyle n}$ Freiheitsgraden ist gegeben durch

${\displaystyle \beta _{2}=3+{\frac {12}{n}}}$.

Der Exzess ${\displaystyle \gamma _{2}}$ gegenüber der Normalverteilung ergibt sich damit zu  ${\displaystyle \gamma _{2}={\tfrac {12}{n}}}$.^[5] Daher gilt: Je höher die Anzahl der Freiheitsgrade ${\displaystyle n}$, desto geringer der Exzess.

Die momenterzeugende Funktion für ${\displaystyle X\sim \chi _{n}^{2}}$ hat die Form^[6]

${\displaystyle M_{X}(t)={\frac {1}{(1-2t)^{n/2}}}}$.

Die charakteristische Funktion für ${\displaystyle X\sim \chi _{n}^{2}}$ ergibt sich aus der momenterzeugenden Funktion als:

${\displaystyle \varphi _{X}(s)={\frac {1}{(1-2is)^{n/2}}}}$.

Die Entropie der Chi-Quadrat-Verteilung (ausgedrückt in nats) beträgt

${\displaystyle H(X)=\ln \left(2\Gamma \left({\frac {n}{2}}\right)\right)+\left(1-{\frac {n}{2}}\right)\psi \left({\frac {n}{2}}\right)+{\frac {n}{2}},}$

wobei ${\displaystyle \psi }$ die Digamma-Funktion bezeichnet.

Wenn die normalverteilten Zufallsvariablen nicht bezüglich ihres Erwartungswertes ${\displaystyle \mu _{i}(i=1,\ldots ,n)}$ zentriert sind (d. h., wenn nicht alle ${\displaystyle \mu _{i}=0}$ sind), erhält man die nichtzentrale Chi-Quadrat-Verteilung. Sie hat als zweiten Parameter neben ${\displaystyle n}$ den Nichtzentralitätsparameter ${\displaystyle \lambda >0}$.

Seien ${\displaystyle Z_{i}\sim {\mathcal {N}}(\mu _{i},1),\,i=1,2,\ldots ,n}$, so ist

${\displaystyle \sum _{i=1}^{n}{Z_{i}}^{2}\sim \chi ^{2}(n,\lambda )}$ mit ${\displaystyle \lambda =\sum _{i=1}^{n}{\mu _{i}}^{2}}$.

Insbesondere folgt aus ${\displaystyle \,X\sim \chi ^{2}(n-1)}$ und ${\displaystyle Z\sim {\mathcal {N}}({\sqrt {\lambda }},1)}$, dass ${\displaystyle \,X+Z^{2}\sim \chi ^{2}(n,\lambda )}$ ist.

Eine zweite Möglichkeit, eine nichtzentrale Chi-Quadrat-Verteilung zu erzeugen, ist als Mischverteilung der zentralen Chi-Quadrat-Verteilung. Dabei ist

${\displaystyle \chi ^{2}(n+2\,j)=\chi ^{2}(n,\lambda )}$,

wenn ${\displaystyle j\sim {\mathcal {P}}\left({\tfrac {\lambda }{2}}\right)}$ aus einer Poisson-Verteilung gezogen wird.

Die Dichtefunktion der nichtzentralen Chi-Quadrat-Verteilung ist

${\displaystyle f(x)={\frac {\exp \left\{-{\frac {1}{2}}(x+\lambda )\right\}}{2^{\frac {n}{2}}}}\,\sum _{j=0}^{\infty }{\frac {x^{{\frac {n}{2}}+j-1}\lambda ^{j}}{2^{2j}\,\Gamma \left({\frac {n}{2}}+j\right)\,j!}}}$ für ${\displaystyle x\geq 0}$ , ${\displaystyle \,f(x)=0}$ für ${\displaystyle \,x<0}$ .

Die Summe über j führt auf eine modifizierte Bessel-Funktion erster Gattung ${\displaystyle I_{q}(x)}$ . Damit erhält die Dichtefunktion folgende Form:

${\displaystyle f(x)={\frac {\exp \left\{-{\frac {1}{2}}(x+\lambda )\right\}x^{{\frac {1}{2}}(n-1)}{\sqrt {\lambda }}}{2(\lambda x)^{\frac {n}{4}}}}\,I_{{\frac {n}{2}}-1}\left({\sqrt {\lambda x}}\right)}$ für ${\displaystyle x\geq 0}$.

Erwartungswert und Varianz der nichtzentralen Chi-Quadrat-Verteilung ${\displaystyle n+\lambda }$ und ${\displaystyle 2n+4\lambda }$ gehen ebenso wie die Dichte selbst bei ${\displaystyle \lambda \to 0}$ in die entsprechenden Ausdrücke der zentralen Chi-Quadrat-Verteilung über.

Die Verteilungsfunktion der nichtzentralen Chi-Quadrat-Verteilung kann mit Hilfe der Marcum-Q-Funktion ${\displaystyle Q_{M}(a,b)}$ ausgedrückt werden:^[7]

${\displaystyle F(x)=1-Q_{\frac {n}{2}}\left({\sqrt {\lambda }},{\sqrt {x}}\right)}$

Gegeben sind ${\displaystyle n}$ Messungen einer Größe ${\displaystyle x}$, die aus einer normalverteilten Grundgesamtheit stammen. Sei ${\displaystyle {\overline {x}}}$ der empirische Mittelwert der ${\displaystyle n}$ gemessenen Werte und

${\displaystyle s^{2}={\frac {1}{n-1}}\sum _{k=1}^{n}(x_{k}-{\overline {x}})^{2}}$

die korrigierte Stichprobenvarianz.

Dann lässt sich z. B. das Konfidenzintervall für die Varianz der Grundgesamtheit ${\displaystyle \sigma ^{2}}$ angeben:

${\displaystyle {\tfrac {n-1}{\chi _{b}^{2}}}\,s^{2}\leq \sigma ^{2}\leq {\tfrac {n-1}{\chi _{a}^{2}}}\,s^{2}}$

Die Grenzen ergeben sich daraus, dass ${\displaystyle {\tfrac {(n-1)s^{2}}{\sigma ^{2}}}}$ wie ${\displaystyle \chi _{n-1}^{2}}$ verteilt ist.

Konkretes Beispiel: Stichprobe mit ${\displaystyle n=100}$ Werten, Varianz ${\displaystyle s^{2}=1{,}0}$ , 95%-Konfidenzintervall:

95 % der Werte sollen sich innerhalb des Intervalls befinden. Es wird also davon ausgegangen, dass je 2,5 % der Werte die obere bzw. untere Intervallgrenze überschreiten dürfen. In diesem Fall wird daher ${\displaystyle \chi _{b}^{2}}$ durch ${\displaystyle F_{n-1}(\chi _{b}^{2})=0{,}975}$ und ${\displaystyle \chi _{a}^{2}}$ durch ${\displaystyle F_{n-1}(\chi _{a}^{2})=0{,}025}$ bestimmt.

Bei der Berechnung der Grenzen des Konfidenzintervalls in Programmen wird üblicherweise die Inverse Funktion verwendet (Kehrwert der kumulierten Chi-Quadrat-Verteilung): z. B. in Excel oder Numbers die Funktion CHIINV(p,n-1) :

Die obere Intervallgrenze ergibt sich mit ${\displaystyle s^{2}=1{,}0}$ aus:

=CHIINV(0,025; 99) / 99 * s^2 = 1,2971

Die untere Intervallgrenze ergibt sich aus:

=CHIINV(0,975; 99) / 99 * s^2 = 0,7410

Sei ${\displaystyle x_{1},\dots ,x_{n}}$ eine Stichprobe von ${\displaystyle n}$ Messwerten, gezogen aus einer normalverteilten Zufallsvariablen ${\displaystyle X}$ mit empirischen Mittelwert ${\displaystyle {\overline {x}}={\tfrac {1}{n}}\sum _{i=1}^{n}x_{i}}$ und Stichprobenvarianz ${\displaystyle s^{2}={\tfrac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}$ als Schätzfunktionen für Erwartungswert ${\displaystyle \mu }$ und Varianz ${\displaystyle \sigma ^{2}}$ der Grundgesamtheit.

Dann lässt sich zeigen, dass ${\displaystyle {\tfrac {(n-1)s^{2}}{\sigma ^{2}}}=\sum _{i=1}^{n}{\tfrac {(x_{i}-{\overline {x}})^{2}}{\sigma ^{2}}}}$ verteilt ist wie ${\displaystyle \chi _{n-1}^{2}}$.

Dazu werden nach Helmert^[8] die ${\displaystyle (x_{i})}$ mittels einer orthonormalen Linearkombination in neue Variablen ${\displaystyle (y_{j})}$ transformiert. Die Transformation lautet:

${\displaystyle y_{1}={\tfrac {1}{\sqrt {2}}}x_{1}-{\tfrac {1}{\sqrt {2}}}x_{2}}$

${\displaystyle y_{2}={\tfrac {1}{\sqrt {6}}}x_{1}+{\tfrac {1}{\sqrt {6}}}x_{2}-{\tfrac {2}{\sqrt {6}}}x_{3}}$

   ${\displaystyle \vdots }$

${\displaystyle y_{n-1}={\tfrac {1}{\sqrt {n(n-1)}}}x_{1}+{\tfrac {1}{\sqrt {n(n-1)}}}x_{2}+\dotsb +{\tfrac {1}{\sqrt {n(n-1)}}}x_{n-1}-{\tfrac {n-1}{\sqrt {n(n-1)}}}x_{n}}$

${\displaystyle y_{n}={\tfrac {1}{\sqrt {n}}}x_{1}+{\tfrac {1}{\sqrt {n}}}x_{2}+\dotsb +{\tfrac {1}{\sqrt {n}}}x_{n-1}+{\tfrac {1}{\sqrt {n}}}x_{n}={\sqrt {n}}\,{\overline {x}}.}$

Die neuen unabhängigen Variablen ${\displaystyle y_{i}}$ sind wie ${\displaystyle X}$ normalverteilt mit gleicher Varianz ${\displaystyle \sigma _{y_{i}}^{2}=\sigma _{x_{i}}^{2}=\sigma ^{2},(i=1,\dots ,n)}$, aber mit Erwartungswert ${\displaystyle \mathrm {E} (y_{i})=0,(i=1,\dots ,n-1),}$ beides aufgrund der Faltungsinvarianz der Normalverteilung.

Außerdem gilt für die Koeffizienten ${\displaystyle a_{ij}}$ in ${\displaystyle y_{i}=\sum _{j=1}^{n}a_{ij}x_{j}}$ (falls ${\displaystyle j>i+1}$ , ist ${\displaystyle a_{ij}=0}$) wegen der Orthonormalität ${\displaystyle \sum _{i=1}^{n}a_{ij}a_{ik}=\delta _{jk}}$ (Kronecker-Delta) und damit

${\displaystyle \sum _{i=1}^{n}y_{i}^{2}=\sum _{i=1}^{n}\sum _{j=1}^{n}a_{ij}x_{j}\sum _{k=1}^{n}a_{ik}x_{k}=\sum _{j=1}^{n}\sum _{k=1}^{n}\delta _{jk}x_{j}x_{k}=\sum _{j=1}^{n}x_{j}^{2}.}$

Deshalb ergibt sich nun für die Summe der Abweichungsquadrate

${\displaystyle (n-1)s^{2}=\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}=\sum _{i=1}^{n}x_{i}^{2}-n{\overline {x}}^{2}=\sum _{i=1}^{n}y_{i}^{2}-y_{n}^{2}=\sum _{i=1}^{n-1}y_{i}^{2}}$

und schlussendlich nach Division durch ${\displaystyle \sigma ^{2}}$

${\displaystyle (n-1){\frac {s^{2}}{\sigma ^{2}}}=\sum _{i=1}^{n-1}{\frac {y_{i}^{2}}{\sigma ^{2}}}.}$

Der Ausdruck auf der linken Seite ist offenbar verteilt wie eine Summe von quadrierten standardnormalverteilten unabhängigen Variablen mit ${\displaystyle n-1}$ Summanden, wie für ${\displaystyle \chi _{n-1}^{2}}$ gefordert.

Demnach ist also die Summe Chi-Quadrat-verteilt mit ${\displaystyle n-1}$ Freiheitsgraden ${\displaystyle \sum _{i=1}^{n}\left({\tfrac {x_{i}-{\overline {x}}}{\sigma }}\right)^{2}\sim \chi _{n-1}^{2}}$, während laut Definition der Chi-Quadrat-Summe ${\displaystyle \sum _{i=1}^{n}\left({\tfrac {x_{i}-\mu }{\sigma }}\right)^{2}\sim \chi _{n}^{2}}$. Ein Freiheitsgrad wird hier „verbraucht“, denn aufgrund der Schwerpunkteigenschaft des empirischen Mittels ${\displaystyle \sum \nolimits _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)=0}$ ist die letzte Abweichung ${\displaystyle \left(x_{n}-{\overline {x}}\right)}$ bereits durch die ersten ${\displaystyle (n-1)}$ bestimmt. Folglich variieren nur ${\displaystyle (n-1)}$ Abweichungen frei und man mittelt die empirische Varianz deshalb, indem man durch die Anzahl der Freiheitsgrade ${\displaystyle (n-1)}$ dividiert.

Die Chi-Quadrat-Verteilung ist ein Spezialfall der Gammaverteilung. Ist ${\displaystyle X\sim \chi _{n}^{2}}$, so gilt

${\displaystyle X\sim {\mathcal {G}}({\tfrac {n}{2}},{\tfrac {1}{2}}).}$

• Seien ${\displaystyle Z_{1},\dotsc ,Z_{n}}$ unabhängige und standardnormalverteilte Zufallsvariablen, dann ist deren Quadratsumme ${\displaystyle Q}$ chi-Quadrat-verteilt mit ${\displaystyle n}$ Freiheitsgraden:

${\displaystyle Q=Z_{1}^{2}+\dotsb +Z_{n}^{2}\;\sim \;\chi ^{2}(n)}$.

• Für ${\displaystyle n\geq 30}$ ist ${\displaystyle Y={\sqrt {2X}}-{\sqrt {2n-1}}}$ näherungsweise standardnormalverteilt.

• Für ${\displaystyle n>100}$ ist die Zufallsvariable ${\displaystyle X_{n}}$ näherungsweise normalverteilt, mit Erwartungswert ${\displaystyle n}$ und Standardabweichung ${\displaystyle {\sqrt {2n}}}$ bzw. bei einer nichtzentralen Chi-Quadrat-Verteilung mit Erwartungswert ${\displaystyle n+\lambda }$ und Standardabweichung ${\displaystyle {\sqrt {2n+4\lambda }}}$.

Eine Chi-Quadrat-Verteilung mit 2 Freiheitsgraden ist eine Exponentialverteilung ${\displaystyle \operatorname {Exp} (\lambda )}$ mit dem Parameter ${\displaystyle \,\lambda =1/2}$.

Eine Chi-Quadrat-Verteilung mit ${\displaystyle 2n}$ Freiheitsgraden ist identisch mit einer Erlang-Verteilung ${\displaystyle \operatorname {Erl} (\lambda ,n)}$ mit ${\displaystyle n}$ Freiheitsgraden und ${\displaystyle \,\lambda =1/2}$.

Seien ${\displaystyle X_{1}}$ und ${\displaystyle X_{2}}$ unabhängige Chi-Quadrat-verteilte Zufallsvariablen mit ${\displaystyle r_{1}}$ bzw. ${\displaystyle r_{2}}$ Freiheitsgraden, dann ist der Quotient

${\displaystyle {\frac {X_{1}/r_{1}}{X_{2}/r_{2}}}}$

F-verteilt mit ${\displaystyle r_{1}}$ Zählerfreiheitsgraden und ${\displaystyle r_{2}}$ Nennerfreiheitsgraden.^[9]

Die Verteilungsfunktionen der Poisson-Verteilung und der Chi-Quadrat-Verteilung hängen auf folgende Weise zusammen:

Die Wahrscheinlichkeit, ${\displaystyle n}$ oder mehr Ereignisse in einem Intervall zu finden, innerhalb dessen man im Mittel ${\displaystyle \lambda }$ Ereignisse erwartet, gleicht der Wahrscheinlichkeit, dass der Wert von ${\displaystyle \chi _{2n}^{2}\leq 2\lambda }$ ist. Es gilt nämlich

${\displaystyle 1-Q(n,\lambda )=P(n,\lambda )}$,

mit ${\displaystyle P}$ und ${\displaystyle Q}$ als regularisierte Gammafunktionen.

Ist ${\displaystyle U}$ gleichverteilt auf dem Intervall ${\displaystyle [0,1]}$, dann gilt ${\displaystyle X=-2\ln(U)\sim \chi ^{2}(2)}$, denn

${\displaystyle P(X\leq x)=P(U\geq \operatorname {exp} (-x/2))=1-\operatorname {exp} (-x/2)=F_{2}(x),\qquad x>0.}$

Sind ${\displaystyle U_{1},\ldots ,U_{m}}$ unabhängig und identisch verteilte Zufallsvariablen mit ${\displaystyle U_{k}\sim {\mathcal {U}}(0,1)}$, dann gilt somit

${\displaystyle -2\sum _{k=1}^{m}\ln(U_{k})\sim \chi ^{2}(2m).}$

Die Dichte der Zufallsvariable ${\displaystyle X=Z_{1}^{2}+\dotsb +Z_{n}^{2}}$, mit ${\displaystyle Z_{1},\dots ,Z_{n}}$ unabhängig und standardnormalverteilt, ergibt sich aus der gemeinsamen Dichte der Zufallsvariablen ${\displaystyle Z_{1},\dots ,Z_{n}}$. Diese gemeinsame Dichte ist das ${\displaystyle n}$-fache Produkt der Standardnormalverteilungsdichte:

${\displaystyle f_{Z_{1},\dots ,Z_{n}}(z_{1},\dots ,z_{n})=\prod _{i=1}^{n}{\frac {e^{-{\frac {1}{2}}z_{i}^{2}}}{\sqrt {2\pi }}}=(2\pi )^{-{\frac {n}{2}}}e^{-{\frac {1}{2}}(z_{1}^{2}+\dotsb +z_{n}^{2})}.}$

Für die gesuchte Dichte gilt:

${\displaystyle {\begin{aligned}f_{n}(x)&=\lim _{h\to 0}{\frac {1}{h}}P(x<X\leq x+h)\\&=\lim _{h\to 0}{\frac {1}{h}}\int \limits _{K}(2\pi )^{-{\frac {n}{2}}}e^{-{\frac {1}{2}}(z_{1}^{2}+\dotsb +z_{n}^{2})}\,dz_{1}\ldots dz_{n}\\&=(2\pi )^{-{\tfrac {n}{2}}}e^{-{\frac {x}{2}}}\lim _{h\to 0}{\frac {1}{h}}\int \limits _{K}dz_{1}\ldots dz_{n}\\\end{aligned}}}$

mit ${\displaystyle K=\{x\leq z_{1}^{2}+\dotsb +z_{n}^{2}\leq x+h\}.}$

Im Grenzwert ist die Summe im Argument der Exponentialfunktion gleich ${\displaystyle x}$. Man kann zeigen, dass man den Integranden als ${\displaystyle (2\pi )^{-{\tfrac {n}{2}}}e^{-{\frac {x}{2}}}}$ vor das Integral und den Limes ziehen kann.

Das verbleibende Integral

${\displaystyle \int \limits _{K}dz_{1}\ldots dz_{n}=V_{n}({\sqrt {x+h}})-V_{n}({\sqrt {x}})}$

entspricht dem Volumen der Schale zwischen der Kugel mit Radius ${\displaystyle {\sqrt {x+h}}}$ und der Kugel mit Radius ${\displaystyle {\sqrt {x}}}$ ,

wobei ${\displaystyle V_{n}(R)={\frac {\pi ^{\frac {n}{2}}R^{n}}{\Gamma ({\frac {n}{2}}+1)}}}$ das Volumen der n-dimensionalen Kugel mit Radius R angibt.

Es folgt: ${\displaystyle \lim _{h\to 0}{\frac {1}{h}}\int \limits _{K}dz_{1}\ldots dz_{n}={\frac {d\,V_{n}({\sqrt {x}})}{d\,x}}={\frac {\pi ^{\tfrac {n}{2}}x^{{\tfrac {n}{2}}-1}}{\Gamma ({\tfrac {n}{2}})}}}$

und nach Einsetzen in den Ausdruck für die gesuchte Dichte: ${\displaystyle f_{n}(x)={\frac {1}{2^{\frac {n}{2}}\Gamma ({\tfrac {n}{2}})}}x^{{\frac {n}{2}}-1}\exp \left(-{\frac {x}{2}}\right)\quad ,x>0}$.

Die Quantilfunktion ${\displaystyle x_{p}}$ der Chi-Quadrat-Verteilung ist die Lösung der Gleichung ${\textstyle p=P\left({\frac {n}{2}},{\frac {x_{p}}{2}}\right)}$ und damit prinzipiell über die Umkehrfunktion zu berechnen. Konkret gilt hier

${\displaystyle x_{p}=2P^{-1}\left({\frac {n}{2}},p\right),}$

mit ${\displaystyle P^{-1}}$ als Inverse der regularisierten unvollständigen Gammafunktion. Dieser Wert ${\displaystyle x_{p}}$ ist in der Quantiltabelle unter den Koordinaten ${\displaystyle p}$ und ${\displaystyle n}$ eingetragen.

Für wenige Werte ${\displaystyle n}$ (1, 2, 4) kann man die Quantilfunktion auch alternativ angeben:

${\displaystyle n=1:x_{p}=2(\operatorname {Erf} ^{-1}(p))^{2},}$

${\displaystyle n=2:x_{p}=-2\,\ln(1-p),}$

${\displaystyle n=4:x_{p}=-2\,(1+W_{-1}(-(1-p)/e)),}$

wobei ${\displaystyle \operatorname {Erf} }$ die Fehlerfunktion, ${\displaystyle W_{-1}(x)\,}$ den unteren Zweig der Lambertschen W-Funktion bezeichnet und ${\displaystyle e}$ die Eulersche Zahl.

Für bestimmte feste Wahrscheinlichkeiten ${\displaystyle p}$ lassen sich die zugehörigen Quantile ${\displaystyle x_{p}}$ durch die einfache Funktion des Stichprobenumfangs ${\displaystyle n}$

${\displaystyle x_{p}\approx n+a{\sqrt {n+\operatorname {sgn}(a){\sqrt {n}}}}+b+c/n}$

mit den Parametern ${\displaystyle a,b,c}$ aus der Tabelle annähern, wobei ${\displaystyle \operatorname {sgn}(a)}$ die Signum-Funktion bezeichnet, die einfach das Vorzeichen ihres Arguments darstellt:

Der Vergleich mit einer ${\displaystyle \chi ^{2}}$-Tabelle zeigt ab ${\displaystyle n>3}$ einen relativen Fehler unter 0,4 %, ab ${\displaystyle n>10}$ unter 0,1 %. Da die ${\displaystyle \chi ^{2}}$-Verteilung für große ${\displaystyle n}$ in eine Normalverteilung mit Standardabweichung ${\displaystyle {\sqrt {2n}}}$ übergeht, besitzt der Parameter ${\displaystyle a}$ aus der Tabelle, der hier frei angepasst wurde, bei der entsprechenden Wahrscheinlichkeit ${\displaystyle p}$ etwa die Größe des ${\displaystyle {\sqrt {2}}}$-fachen des Quantils der Normalverteilung (${\displaystyle {\sqrt {2}}\,\operatorname {Erf} ^{-1}(2p-1)}$), wobei ${\displaystyle \operatorname {Erf} ^{-1}}$ die Umkehrfunktion der Fehlerfunktion bedeutet.

Das 95 %-Konfidenzintervall für die Varianz der Grundgesamtheit aus dem Abschnitt Beispiel kann z. B. mit den beiden Funktionen ${\displaystyle x_{p}}$ aus den Zeilen mit ${\displaystyle p=0{,}025\to \chi _{a}^{2}}$ und ${\displaystyle p=0{,}975\to \chi _{b}^{2}}$ auf einfache Weise als Funktion von ${\displaystyle n}$ grafisch dargestellt werden.

Der Median befindet sich in der Spalte der Tabelle mit ${\displaystyle p=0{,}5}$.

• Joachim Hartung, Bärbel Elpelt, Karl-Heinz Klösener: Statistik. 12. Auflage. Oldenbourg, 1999, ISBN 3-486-24984-3, S. 152 ff. 

Wikibooks: Tabelle der χ²-Verteilung (Quantiltabelle) – Lern- und Lehrmaterialien

1. ↑ R. Barlow: Statistics Wiley, 1989, S. 152 (Goodness of Fit).
2. ↑ Kendall, Stuart: The Advanced Theory Of Statistics Vol. 2 Third Edition, London, 1973, S. 436 (Goodness of Fit).
3. ↑ F. R. Helmert. In: Zeitschrift fuer Math. und Physik 21, 1876, S. 192–219. Karl Pearson: On the Criterion that a Given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it Can Reasonably Be Supposed to have Arisen from Random Sampling. In: Philosophical Magazine 5, Band 50, 1900, S. 157–175. Zitiert nach L. Schmetterer: Mathematische Statistik. Springer, Wien 1966, S. 93
4. ↑ ^{a b} Ilja Nikolajewitsch Bronstein, Konstantin Adolfowitsch Semendjajew: Taschenbuch der Mathematik. 5. Auflage. Verlag Harri Deutsch, 2000, ISBN 3-8171-2005-2, S. 782. 
5. ↑ Wolfram Mathworld
6. ↑ A. C. Davison: Statistical Models, Cambridge University Press 2008, ISBN 1-4672-0331-9, Kapitel 3.2
7. ↑ Albert H. Nuttall: Some Integrals Involving the Q_M Function. In: IEEE Transactions on Information Theory. Nr. 21, 1975, S. 95–96, doi:10.1109/TIT.1975.1055327.
8. ↑ Helmert. In: Astronomische Nachrichten, 88, 1876, S. 113–132
9. ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee. Introduction to the Theory and Practice of Econometrics. 2. Auflage. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore 1988, ISBN 0-471-62414-4, S. 51.