Als Bessel-Funktionen bezeichnet man Funktionen, welche Lösungen der besselschen Differentialgleichung sind, die eine lineare gewöhnliche Differentialgleichung zweiter Ordnung ist. Benannt sind die Funktionen und die Gleichung nach dem deutschen Mathematiker Friedrich Wilhelm Bessel . Die Bessel-Funktionen werden auch Zylinderfunktionen genannt.
Besselsche Differentialgleichung Die Besselsche Differentialgleichung ist eine gewöhnliche lineare Differentialgleichung zweiter Ordnung, die durch
x 2 d 2 f d x 2 + x d f d x + ( x 2 − ν 2 ) f = 0 {\displaystyle x^{2}{\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} f}{\mathrm {d} x}}+\left(x^{2}-\nu ^{2}\right)f=0} definiert ist, wobei x {\displaystyle x} ν {\displaystyle \nu } Zahlen sind. Die Lösungen heißen Bessel-Funktionen ν {\displaystyle \nu } .
Entsprechend ist der Bessel-Operator ein Differentialoperator zweiter Ordnung. Er ist definiert durch
B ν := x 2 d 2 d x 2 + x d d x + ( x 2 − ν 2 ) . {\displaystyle B_{\nu }:=x^{2}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} }{\mathrm {d} x}}+\left(x^{2}-\nu ^{2}\right)\,.} Mit ihm kann man die Besselsche Differentialgleichung kurz ausdrücken durch[ 1]
B ν f = 0 {\displaystyle B_{\nu }f=0}
Bessel-Funktionen
Allgemein Die Bessel-Funktionen erster Gattung J 0 , J 1 {\displaystyle J_{0},J_{1}} J 2 {\displaystyle J_{2}} Die Bessel-Funktionen zweiter Gattung Y 0 , Y 1 {\displaystyle Y_{0},Y_{1}} Y 2 {\displaystyle Y_{2}} Die Lösungen der Besselschen Differentialgleichung heißen Bessel-Funktionen . Sie spielen eine wichtige Rolle in der Physik, da die Besselsche Differentialgleichung den radialen Anteil der Laplace-Gleichung bei zylindrischer Symmetrie darstellt. Auf die Bessel-Funktionen trifft man unter anderem bei der Untersuchung von Eigenschwingungen einer kreisförmigen Membran oder einer Orgelpfeife, der Ausbreitung von Wasserwellen in runden Behältern, der Wärmeleitung in Stäben, der Analyse des Frequenzspektrums frequenzmodulierter Signale, der Feldverteilung im Querschnitt von Rundhohlleitern , den stationären Zuständen von Kastenpotentialen, der Leistungsverteilung in Kernreaktoren , der Intensität von Lichtbeugung an kreisförmigen Löchern sowie bei Filtern in der Elektrotechnik (Bessel-Filter ). Man zählt die Bessel-Funktionen wegen ihrer vielfältigen Anwendungen in der mathematischen Physik zu den speziellen Funktionen .
Als Differentialgleichung zweiter Ableitungsordnung besitzt die Besselsche Differentialgleichung zwei linear unabhängige Lösungen . Sie lassen sich in verschiedenen Varianten beschreiben.
Jν Die Bessel-Funktion J ν {\displaystyle J_{\nu }} ν {\displaystyle \nu }
J ν ( x ) = ∑ r = 0 ∞ ( − 1 ) r ( x 2 ) 2 r + ν Γ ( ν + r + 1 ) r ! {\displaystyle J_{\nu }(x)=\sum _{r=0}^{\infty }{\frac {(-1)^{r}\left({\frac {x}{2}}\right)^{2r+\nu }}{\Gamma (\nu +r+1)r!}}\,} wobei Γ ( ⋅ ) {\displaystyle \Gamma (\cdot )} Gammafunktion ist. Im Ursprung (x = 0 {\displaystyle x=0} ν {\displaystyle \nu }
Für nicht-ganzzahlige ν {\displaystyle \nu } J ν {\displaystyle J_{\nu }} J − ν {\displaystyle J_{-\nu }}
Für ganzzahlige ν {\displaystyle \nu }
J − ν ( x ) = ( − 1 ) ν J ν ( x ) = J ν ( − x ) {\displaystyle J_{-\nu }(x)=(-1)^{\nu }J_{\nu }(x)=J_{\nu }(-x)\,} In diesem Fall ist die zweite unabhängige Lösung die Bessel-Funktion zweiter Gattung, die weiter unten diskutiert wird.
Integraldarstellungen Für ganzzahlige ν {\displaystyle \nu }
J ν ( x ) = 1 π ∫ 0 π cos ( ν φ ) cos [ x sin ( φ ) ] + sin ( ν φ ) sin [ x sin ( φ ) ] d φ {\displaystyle J_{\nu }(x)={\frac {1}{\pi }}\int _{0}^{\pi }\cos(\nu \,\varphi )\cos {\bigl [}x\sin(\varphi ){\bigr ]}+\sin(\nu \,\varphi )\sin {\bigl [}x\sin(\varphi ){\bigr ]}\,\mathrm {d} \varphi } Mit dem Additionstheorem der Kosinusfunktion kann dann noch folgende Vereinfachung vorgenommen werden:
J ν ( x ) = 1 π ∫ 0 π cos ( x sin φ − ν φ ) d φ = 1 2 π ∫ − π π e i ( x sin φ − ν φ ) d φ . {\displaystyle {\begin{aligned}J_{\nu }(x)&={\frac {1}{\pi }}\int _{0}^{\pi }\cos(x\sin \varphi -\nu \varphi )\,\mathrm {d} \varphi \\&={\frac {1}{2\pi }}\int _{-\pi }^{\pi }e^{\mathrm {i} \,(x\sin \varphi -\nu \varphi )}\,\mathrm {d} \varphi \,.\end{aligned}}} Damit ist J ν ( x ) {\displaystyle J_{\nu }(x)} ν {\displaystyle \nu } Fourier-Koeffizient der Funktion φ ↦ e i x sin φ {\displaystyle \varphi \mapsto e^{ix\sin \varphi }}
Exemplarisch wird im Folgenden die Bessel-Funktion J 0 {\displaystyle J_{0}}
J 0 ( x ) = ∑ n = 0 ∞ ( − 1 ) n x 2 n 4 n ( n ! ) 2 = ∫ 0 π 1 π cos [ x sin ( y ) ] d y = ∫ 0 1 2 cos ( x z ) π 1 − z 2 d z {\displaystyle J_{0}(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{4^{n}(n!)^{2}}}=\int _{0}^{\pi }{\frac {1}{\pi }}\cos {\bigl [}x\sin(y){\bigr ]}\,\mathrm {d} y=\int _{0}^{1}{\frac {2\cos(xz)}{\pi {\sqrt {1-z^{2}}}}}\,\mathrm {d} z}
Hypergeometrische Funktion Die Bessel-Funktion erster Gattung kann durch die verallgemeinerte hypergeometrische Funktion ausgedrückt werden:
J ν ( x ) = ( x / 2 ) ν Γ ( ν + 1 ) 0 F 1 ( ; ν + 1 ; − x 2 / 4 ) . {\displaystyle J_{\nu }(x)={\frac {(x/2)^{\nu }}{\Gamma (\nu +1)}}\;_{0}F_{1}(;\nu +1;-x^{2}/4).} Dieser Ausdruck hängt mit der Entwicklung der Bessel-Funktion in Abhängigkeit zur Bessel-Clifford-Funktion zusammen.
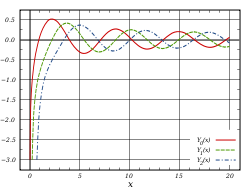
Yν Auch die Bessel-Funktionen zweiter Gattung Y ν ( x ) {\displaystyle Y_{\nu }(x)} Weber -Funktionen oder Neumann -Funktionen genannt) lösen die Besselsche Differentialgleichung. Eine alternative Bezeichnung ist N ν ( x ) {\displaystyle N_{\nu }(x)} ν {\displaystyle \nu } Y ν ( x ) {\displaystyle Y_{\nu }(x)}
Y ν ( x ) = J ν ( x ) cos ( ν π ) − J − ν ( x ) sin ( ν π ) . {\displaystyle Y_{\nu }(x)={\frac {J_{\nu }(x)\cos(\nu \pi )-J_{-\nu }(x)}{\sin(\nu \pi )}}.} Für ganzzahlige n {\displaystyle n} ν → n {\displaystyle \nu \rightarrow n} Funktion
Y n ( x ) = lim ν → n Y ν ( x ) {\displaystyle Y_{n}(x)=\lim _{\nu \to n}Y_{\nu }(x)} weiterhin eine Lösung der Besselschen Differentialgleichung.
Wie für die Bessel-Funktionen erster Gattung gilt auch für die Besselfunktionen zweiter Gattung folgende Beziehung:
Y − n ( x ) = ( − 1 ) n Y n ( x ) {\displaystyle Y_{-n}(x)=(-1)^{n}Y_{n}(x)} Nach Ausführung des Grenzüberganges mit der Regel von de L’Hospital ergibt sich
Y n ( x ) = 1 π [ d d ν J ν ( x ) | ν = n + ( − 1 ) n d d ν J ν ( x ) | ν = − n ] . {\displaystyle Y_{n}(x)={\frac {1}{\pi }}\left[{\operatorname {d} \over \operatorname {d} \!\nu }J_{\nu }(x){\Big |}_{\nu =n}+(-1)^{n}{\operatorname {d} \over \operatorname {d} \!\nu }J_{\nu }(x){\Big |}_{\nu =-n}\right].} Explizit findet man
Y n ( x ) = 2 π ( γ + ln x 2 ) J n ( x ) − 1 π ∑ k = 0 n − 1 ( n − k − 1 ) ! k ! ( x 2 ) 2 k − n − 1 π ∑ k = 0 ∞ ( − 1 ) k H k + H k + n k ! ( n + k ) ! ( x 2 ) 2 k + n {\displaystyle Y_{n}(x)=\,{\frac {2}{\pi }}\left(\gamma +\ln {\frac {x}{2}}\right)J_{n}(x)-{\frac {1}{\pi }}\sum _{k=0}^{n-1}{\frac {(n-k-1)!}{k!}}\left({\frac {x}{2}}\right)^{2k-n}-{\frac {1}{\pi }}\sum _{k=0}^{\infty }(-1)^{k}{\frac {H_{k}+H_{k+n}}{k!(n+k)!}}\left({\frac {x}{2}}\right)^{2k+n}} für n ∈ N 0 {\displaystyle n\in \mathbb {N} _{0}} γ {\displaystyle \gamma } Euler-Mascheroni-Konstante und H n {\displaystyle H_{n}} n {\displaystyle n} harmonische Zahl .
Die Bessel-Funktionen zweiter Gattung haben also bei x = 0 {\displaystyle x=0} n {\displaystyle n}
Für alle ν {\displaystyle \nu } J ν {\displaystyle J_{\nu }} Y ν {\displaystyle Y_{\nu }}
Hν (1) , Hν (2) Die Bessel-Funktionen dritter Gattung H ν ( 1 ) {\displaystyle H_{\nu }^{(1)}} H ν ( 2 ) {\displaystyle H_{\nu }^{(2)}} Hankel -Funktionen) sind Linearkombinationen der Bessel-Funktionen erster und zweiter Gattung
H ν ( 1 ) ( x ) = J ν ( x ) + i ⋅ Y ν ( x ) , H ν ( 2 ) ( x ) = J ν ( x ) − i ⋅ Y ν ( x ) , {\displaystyle {\begin{aligned}H_{\nu }^{(1)}(x)&=J_{\nu }(x)+\mathrm {i} \cdot Y_{\nu }(x)\,,\\H_{\nu }^{(2)}(x)&=J_{\nu }(x)-\mathrm {i} \cdot Y_{\nu }(x)\,,\end{aligned}}} wobei i {\displaystyle \mathrm {i} } imaginäre Einheit bezeichnet. Auch diese beiden Funktionen sind linear unabhängige Lösungen der Besselschen Differentialgleichung.
Eigenschaften
Beziehungen von Ordnungen einer Gattung Für die Bessel-Funktionen J ν {\displaystyle J_{\nu }} Y ν {\displaystyle Y_{\nu }} H ν ( 1 ) {\displaystyle H_{\nu }^{(1)}} H ν ( 2 ) {\displaystyle H_{\nu }^{(2)}} Rekursionsbeziehungen : ν x Ω ν = 1 2 ( Ω ν − 1 + Ω ν + 1 ) {\displaystyle {\frac {\nu }{x}}\Omega _{\nu }={\frac {1}{2}}(\Omega _{\nu -1}+\Omega _{\nu +1})} d d x Ω ν = 1 2 ( Ω ν − 1 − Ω ν + 1 ) {\displaystyle {\frac {\rm {d}}{{\rm {d}}x}}\Omega _{\nu }={\frac {1}{2}}(\Omega _{\nu -1}-\Omega _{\nu +1})} Für x ∈ R {\displaystyle x\in \mathbb {R} } ∑ n = − ∞ ∞ J n ( x ) 2 = 1 {\displaystyle \sum _{n=-\infty }^{\infty }J_{n}(x)^{2}=1} Für n ∈ N {\displaystyle n\in \mathbb {N} } ( − 1 x d d x ) n J 0 ( x ) = J n ( x ) x n {\displaystyle \left(-{\frac {1}{x}}{\frac {\rm {d}}{{\rm {d}}x}}\right)^{n}J_{0}(x)={\frac {J_{n}(x)}{x^{n}}}}
Asymptotisches Verhalten Seien x , ν ∈ R , ν ≥ 0 {\displaystyle x,\nu \in \mathbb {R} ,\nu \geq 0} 0 < x ≪ ν + 1 {\displaystyle 0<x\ll {\sqrt {\nu +1}}}
J ν ( x ) ≈ 1 Γ ( ν + 1 ) ( x 2 ) ν Y ν ( x ) ≈ { 2 π ( ln ( x 2 ) + γ ) wenn ν = 0 − Γ ( ν ) π ( 2 x ) ν wenn ν > 0. {\displaystyle {\begin{aligned}J_{\nu }(x)&\approx {\frac {1}{\Gamma (\nu +1)}}\left({\frac {x}{2}}\right)^{\nu }\\Y_{\nu }(x)&\approx {\begin{cases}{\frac {2}{\pi }}\left(\ln \left({\frac {x}{2}}\right)+\gamma \right)&{\text{wenn }}\nu =0\\\\-{\frac {\Gamma (\nu )}{\pi }}\left({\frac {2}{x}}\right)^{\nu }&{\text{wenn }}\nu >0.\end{cases}}\end{aligned}}} Für große Argumente x ≫ | ν 2 − 1 / 4 | {\displaystyle x\gg |\nu ^{2}-1/4|}
J ν ( x ) ≈ 2 π x cos ( x − ν π 2 − π 4 ) Y ν ( x ) ≈ 2 π x sin ( x − ν π 2 − π 4 ) . {\displaystyle {\begin{aligned}J_{\nu }(x)&\approx {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\nu \pi }{2}}-{\frac {\pi }{4}}\right)\\Y_{\nu }(x)&\approx {\sqrt {\frac {2}{\pi x}}}\sin \left(x-{\frac {\nu \pi }{2}}-{\frac {\pi }{4}}\right).\end{aligned}}} Diese Formeln sind für ν = 1 / 2 {\displaystyle \nu =1/2}
Iν , Kν Die modifizierten Bessel-Funktionen erster Gattung für I 0 , I 1 , I 2 {\displaystyle I_{0},I_{1},I_{2}} I 3 {\displaystyle I_{3}} Die modifizierten Bessel-Funktionen zweiter Gattung für K 0 , K 1 , K 2 {\displaystyle K_{0},K_{1},K_{2}} K 3 {\displaystyle K_{3}} Die Differentialgleichung
x 2 d 2 f d x 2 + x d f d x − ( x 2 + ν 2 ) f = 0 {\displaystyle x^{2}{\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} f}{\mathrm {d} x}}-(x^{2}+\nu ^{2})f=0} wird durch Bessel-Funktionen mit rein imaginärem Argument gelöst. Man definiert für ihre Lösung normalerweise die modifizierten Bessel-Funktionen
I ν ( x ) = i − ν J ν ( i x ) = ∑ r = 0 ∞ ( x 2 ) 2 r + ν Γ ( r + ν + 1 ) r ! {\displaystyle I_{\nu }(x)=i^{-\nu }J_{\nu }(ix)=\sum _{r=0}^{\infty }{\frac {({\frac {x}{2}})^{2r+\nu }}{\Gamma (r+\nu +1)r!}}} I ν ( x ) = 1 π ∫ 0 π cos ( ν φ ) cosh [ x sin ( φ ) ] − sin ( ν φ ) sinh [ x sin ( φ ) ] d φ {\displaystyle I_{\nu }(x)={\frac {1}{\pi }}\int _{0}^{\pi }\cos(\nu \,\varphi )\cosh {\bigl [}x\sin(\varphi ){\bigr ]}-\sin(\nu \,\varphi )\sinh {\bigl [}x\sin(\varphi ){\bigr ]}\,\mathrm {d} \varphi } und
K ν ( x ) = π 2 I − ν ( x ) − I ν ( x ) sin ( ν π ) = π 2 i ν + 1 H ν ( 1 ) ( i x ) = π 2 ( − i ) ν + 1 H ν ( 2 ) ( − i x ) . {\displaystyle {\begin{aligned}K_{\nu }(x)={\frac {\pi }{2}}{\frac {I_{-\nu }(x)-I_{\nu }(x)}{\sin(\nu \pi )}}={\frac {\pi }{2}}i^{\nu +1}H_{\nu }^{(1)}(ix)={\frac {\pi }{2}}(-i)^{\nu +1}H_{\nu }^{(2)}(-ix).\end{aligned}}} K ν ( x ) {\displaystyle K_{\nu }(x)} MacDonald-Funktion bekannt. Anders als die „normalen“ Besselfunktionen weisen die modifizierten Besselfunktionen kein oszillierendes, sondern ein exponentielles Verhalten auf.
Exemplarisch wird im Folgenden Bessel-Funktionen I 0 {\displaystyle I_{0}}
I 0 ( x ) = ∑ n = 0 ∞ x 2 n 4 n ( n ! ) 2 = ∫ 0 π 1 π cosh [ x sin ( y ) ] d y = ∫ 0 1 2 cosh ( x z ) π 1 − z 2 d z {\displaystyle I_{0}(x)=\sum _{n=0}^{\infty }{\frac {x^{2n}}{4^{n}(n!)^{2}}}=\int _{0}^{\pi }{\frac {1}{\pi }}\cosh {\bigl [}x\sin(y){\bigr ]}\,\mathrm {d} y=\int _{0}^{1}{\frac {2\cosh(xz)}{\pi {\sqrt {1-z^{2}}}}}\,\mathrm {d} z}
Airysche Integrale Für die Funktionen K 1 / 3 {\displaystyle K_{1/3}} K 2 / 3 {\displaystyle K_{2/3}}
K 1 / 3 ( x ) = 3 ∫ 0 ∞ cos ( 3 2 x ( u + u 3 3 ) ) d u K 2 / 3 ( x ) = 3 ∫ 0 ∞ u sin ( 3 2 x ( u + u 3 3 ) ) d u {\displaystyle {\begin{aligned}K_{1/3}(x)&={\sqrt {3}}\int _{0}^{\infty }\cos \left({\frac {3}{2}}x\left(u+{\frac {u^{3}}{3}}\right)\right)\mathrm {d} u\\K_{2/3}(x)&={\sqrt {3}}\int _{0}^{\infty }u\sin \left({\frac {3}{2}}x\left(u+{\frac {u^{3}}{3}}\right)\right)\mathrm {d} u\end{aligned}}}
Hypergeometrische Funktion Auch die modifizierte Bessel-Funktion erster Gattung kann durch eine verallgemeinerte hypergeometrische Funktion ausgedrückt werden:
I ν ( x ) = ( x / 2 ) ν Γ ( ν + 1 ) 0 F 1 ( ν + 1 ; x 2 / 4 ) {\displaystyle I_{\nu }(x)={\frac {(x/2)^{\nu }}{\Gamma (\nu +1)}}\;_{0}F_{1}(\nu +1;x^{2}/4)}
Beziehungen von Ordnungen einer Gattung Für die Bessel-Funktionen K ν {\displaystyle K_{\nu }} I ν {\displaystyle I_{\nu }} Rekursionsbeziehungen : ν x K ν = − 1 2 ( K ν − 1 − K ν + 1 ) {\displaystyle {\frac {\nu }{x}}K_{\nu }=-{\frac {1}{2}}\left(K_{\nu -1}-K_{\nu +1}\right)} ν x I ν = 1 2 ( I ν − 1 − I ν + 1 ) {\displaystyle {\frac {\nu }{x}}I_{\nu }={\frac {1}{2}}\left(I_{\nu -1}-I_{\nu +1}\right)} d d x K ν = − 1 2 ( K ν − 1 + K ν + 1 ) {\displaystyle {\frac {\rm {d}}{{\rm {d}}x}}K_{\nu }=-{\frac {1}{2}}(K_{\nu -1}+K_{\nu +1})} d d x I ν = 1 2 ( I ν − 1 + I ν + 1 ) {\displaystyle {\frac {\rm {d}}{{\rm {d}}x}}I_{\nu }={\frac {1}{2}}(I_{\nu -1}+I_{\nu +1})}
Asymptotisches Verhalten Wir nehmen wieder an, dass ν {\displaystyle \nu } 0 < x ≪ ν + 1 {\displaystyle 0<x\ll {\sqrt {\nu +1}}}
I ν ( x ) ≈ 1 Γ ( ν + 1 ) ( x 2 ) ν K ν ( x ) ≈ { − ( ln ( x 2 ) + γ ) wenn ν = 0 Γ ( ν ) 2 ( 2 x ) ν wenn ν > 0 . {\displaystyle {\begin{aligned}I_{\nu }(x)&\approx {\frac {1}{\Gamma (\nu +1)}}\left({\frac {x}{2}}\right)^{\nu }\\\\K_{\nu }(x)&\approx {\begin{cases}-\left(\ln \left({\frac {x}{2}}\right)+\gamma \right)&{\text{wenn }}\nu =0\\\\{\frac {\Gamma (\nu )}{2}}\left({\frac {2}{x}}\right)^{\nu }&{\text{wenn }}\nu >0\,.\end{cases}}\end{aligned}}} Für große Argumente x ≫ | ν 2 − 1 / 4 | {\displaystyle x\gg |\nu ^{2}-1/4|}
I ν ( x ) ≈ 1 2 π x e x ( 1 + O ( 1 x ) ) K ν ( x ) ≈ π 2 x e − x ( 1 + O ( 1 x ) ) . {\displaystyle {\begin{aligned}I_{\nu }(x)&\approx {\frac {1}{\sqrt {2\pi x}}}e^{x}\left(1+{\mathcal {O}}\left({\frac {1}{x}}\right)\right)\\\\K_{\nu }(x)&\approx {\sqrt {\frac {\pi }{2x}}}e^{-x}\left(1+{\mathcal {O}}\left({\frac {1}{x}}\right)\right)\,.\end{aligned}}}
jμ , yμ , hμ (1,2) Die Helmholtz-Gleichung in Kugelkoordinaten führt nach Separation der Variablen auf die Radialgleichung
x 2 d 2 f μ ( x ) d x 2 + 2 x d f μ ( x ) d x + [ x 2 − μ ( μ + 1 ) ] f μ ( x ) = 0 {\displaystyle x^{2}{\frac {\mathrm {d} ^{2}f_{\mu }(x)}{\mathrm {d} x^{2}}}+2x{\frac {\mathrm {d} f_{\mu }(x)}{\mathrm {d} x}}+[x^{2}-\mu (\mu +1)]f_{\mu }(x)=0} Nach der Substitution
f μ ( x ) = 1 x u μ ( x ) {\displaystyle f_{\mu }(x)={\frac {1}{\sqrt {x}}}u_{\mu }(x)} erhält man die Besselsche Differentialgleichung ( ν = μ + 1 / 2 ) {\displaystyle (\nu =\mu +1/2)}
x 2 d 2 u μ ( x ) d x 2 + x d u μ ( x ) d x + [ x 2 − ( μ + 1 2 ) 2 ] u μ ( x ) = 0 {\displaystyle x^{2}{\frac {\mathrm {d} ^{2}u_{\mu }(x)}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} u_{\mu }(x)}{\mathrm {d} x}}+\left[x^{2}-\left(\mu +{\frac {1}{2}}\right)^{2}\right]u_{\mu }(x)=0} Für die Lösung f μ ( x ) {\displaystyle f_{\mu }(x)} j μ ( x ) {\displaystyle j_{\mu }(x)} y μ ( x ) = n μ ( x ) {\displaystyle y_{\mu }(x)=n_{\mu }(x)} h μ ( 1 , 2 ) ( x ) {\displaystyle h_{\mu }^{(1,2)}(x)}
j μ ( x ) = π 2 x J μ + 1 / 2 ( x ) y μ ( x ) = π 2 x Y μ + 1 / 2 ( x ) h μ ( 1 , 2 ) ( x ) = π 2 x H μ + 1 / 2 ( 1 , 2 ) = j μ ( x ) ± i y μ ( x ) {\displaystyle {\begin{aligned}&j_{\mu }(x)\quad ={\sqrt {\frac {\pi }{2x}}}J_{\mu +1/2}(x)\\&y_{\mu }(x)\quad ={\sqrt {\frac {\pi }{2x}}}Y_{\mu +1/2}(x)\\&h_{\mu }^{(1,2)}(x)={\sqrt {\frac {\pi }{2x}}}H_{\mu +1/2}^{(1,2)}=j_{\mu }(x)\pm iy_{\mu }(x)\end{aligned}}} m ∈ N {\displaystyle m\in \mathbb {N} }
j m ( x ) = ( − x ) m ( 1 x d d x ) m sin x x y m ( x ) = − ( − x ) m ( 1 x d d x ) m cos x x h m ( 1 , 2 ) ( x ) = ∓ i ( − x ) m ( 1 x d d x ) m e ± i x x {\displaystyle {\begin{aligned}&j_{m}(x)\quad =(-x)^{m}\left({\frac {1}{x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{m}\ {\frac {\sin x}{x}}\\&y_{m}(x)\quad =-(-x)^{m}\left({\frac {1}{x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{m}\ {\frac {\cos x}{x}}\\&h_{m}^{(1,2)}(x)=\mp i(-x)^{m}\left({\frac {1}{x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{m}{\frac {e^{\pm ix}}{x}}\\\end{aligned}}} Die sphärischen Bessel- und Hankelfunktionen werden beispielsweise für die Behandlung des kugelsymmetrischen Potentialtopfs in der Quantenmechanik benötigt.
Eigenschaften Für die sphärischen Bessel-Funktionen j μ {\displaystyle j_{\mu }} y μ {\displaystyle y_{\mu }} h μ ( 1 ) {\displaystyle h_{\mu }^{(1)}} h μ ( 2 ) {\displaystyle h_{\mu }^{(2)}} Rekursionsbeziehungen : 2 μ + 1 x ω μ ( x ) = ω μ − 1 ( x ) + ω μ + 1 ( x ) ( 2 μ + 1 ) ω μ ′ ( x ) = μ ω μ − 1 ( x ) − ( μ + 1 ) ω μ + 1 ( x ) d d x ( x ω μ ( x ) ) = x ω μ − 1 ( x ) − μ ω μ ( x ) {\displaystyle {\begin{aligned}&{\frac {2\mu +1}{x}}\omega _{\mu }(x)\;\,=\omega _{\mu -1}(x)+\omega _{\mu +1}(x)\\&(2\mu +1)\omega '_{\mu }(x)\,=\mu \omega _{\mu -1}(x)-(\mu +1)\omega _{\mu +1}(x)\\&{\frac {\mathrm {d} }{\mathrm {d} x}}(x\omega _{\mu }(x))\quad =x\omega _{\mu -1}(x)-\mu \omega _{\mu }(x)\end{aligned}}} W ( j μ , y μ ) = 1 i W ( j μ , h μ ( 1 ) ) = − W ( y μ , h μ ( 1 ) ) = 1 x 2 {\displaystyle W(j_{\mu },y_{\mu })={\frac {1}{i}}W(j_{\mu },h_{\mu }^{(1)})=-W(y_{\mu },h_{\mu }^{(1)})={\frac {1}{x^{2}}}}
Die Hankel-Transformation ist eine Integraltransformation , die eng mit der Fourier-Transformation verwandt ist. Der Integralkern der Hankel-Transformation ist die Bessel-Funktion erster Gattung J n {\displaystyle J_{n}}
H n [ f ] ( s ) = ∫ 0 ∞ J n ( t s ) t f ( t ) d t {\displaystyle H_{n}[f](s)=\int _{0}^{\infty }J_{n}(ts)tf(t)\mathrm {d} t} Eine besondere Eigenschaft der Hankel-Transformation ist, dass mit ihr der Bessel-Operator in einen algebraischen Ausdruck (eine Multiplikation) überführt werden kann.
Geschichte Bessel-Funktionen wurden von Bessel 1824 ausführlich behandelt,[ 2] Daniel Bernoulli (Schwingung schwerer Ketten 1738), Leonhard Euler (Membranschwingung 1764), in der Himmelsmechanik bei Joseph-Louis Lagrange (1770) und bei Pierre-Simon Laplace , in der Wärmeleitung bei Joseph Fourier (Wärmeausbreitung im Zylinder 1822) und Siméon Denis Poisson (1823).[ 3] [ 4]
Literatur Milton Abramowitz , Irene Stegun : Handbook of Mathematical Functions. Dover, New York 1972, S. 355 .J. H. Graf, E. Gubler: Einleitung in die Theorie der Bessel’schen Funktionen. Erster Band Zweiter Band . K. J. Wyss, Bern 1900 Carl Gottfried Neumann : Theorie der Besselschen Funktionen, ein Analogon zur Theorie der Kugelfunktionen. B. G. Teubner, Leipzig 1867.Paul Schafheitlin Die Theorie der Besselschen Funktionen .G. N. Watson A Treatise on the Theory of Bessel functions , Cambridge University Press 1922, 1944, Archive Besselfunktionen werden in vielen Lehrbüchern der Theoretischen Physik behandelt z. B.:
John David Jackson : Classical Electrodynamics. John Wiley, New York NY 1962 (3. edition. ebenda 1999, ISBN 0-471-30932-X ; deutsch: 4. überarbeitete Auflage. de Gruyter, Berlin u. a. 2006, ISBN 3-11-018970-4 ).Wolfgang Nolting: Grundkurs Theoretische Physik 5/2. Quantenmechanik – Methoden und Anwendungen , 6. Auflage, Springer-Lehrbuch, 2006, ISBN 978-3-540-26035-6 Arnold Sommerfeld Vorlesungen über Theoretische Physik , Band 6: Partielle Differentialgleichungen der Physik , Harri Deutsch 1992, ISBN 3-87144-379-4 .
Einzelnachweise ↑ Bessel-Operator . In: Guido Walz (Hrsg.): Lexikon der Mathematik . 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 978-3-8274-0439-8 . ↑ Friedrich Wilhelm Bessel: Untersuchung des Theils der planetarischen Störungen, welcher aus der Bewegung der Sonne entsteht. ↑ Jacques Dutka: On the early history of Bessel functions. In: Archive for History of Exact Sciences . ↑ G. N. Watson: Theory of Bessel Functions. Cambridge University Press, 1944, Kapitel 1 (zur Geschichte).
Weblinks