Bell-Test
Ein Bell-Test (auch: Bell-Experiment oder Test der Bell'schen Ungleichung) ist ein physikalisches Experiment, das dazu dient, zwischen den Vorhersagen der Quantenmechanik und denen lokal-realistischer Theorien (auch als Lokale-Verborgene-Variablen Theorien bezeichnet) zu unterscheiden. Der Test weist die Verletzung einer Bellschen Ungleichung nach. Diese Ungleichung wird von allen lokal-realistischen Theorien erfüllt, sie wird aber von verschränkten Systemen der Quantenmechanik verletzt.
Bell bewies 1964, dass die Resultate bestimmter Experimente (der später so genannten Bell-Tests) quantifizierbaren Einschränkungen unterliegen, wenn sich die untersuchten Systeme gemäß den Annahmen des lokalen Realismus verhalten. Diese Einschränkungen werden von den Vorhersagen der Quantenmechanik für verschränkte Systeme verletzt. Wenn ein solcher Bell-Test im Labor ausgeführt wird und die erhaltenen Resultate diesen Einschränkungen nicht genügen, dann sind die Ergebnisse mit der Hypothese lokaler verborgener Variablen nicht konsistent und stützen damit die Position, dass es nicht möglich ist, eine lokal-realistische Erklärung für die beobachteten und von der Quantenmechanik beschriebenen Phänomene zu finden.
Seit den frühen 1970er Jahren sind eine Vielzahl solcher Tests auf der ganzen Welt durchgeführt worden und haben jeweils Ergebnisse in Übereinstimmung mit der Quantenmechanik geliefert. Über die Jahre wurden die Experimente immer weiter verbessert, um sogenannte „Schlupflöcher“ zu schließen. Damit werden Abweichungen des tatsächlichen experimentellen Aufbaus von den idealen Voraussetzungen, auf denen der Beweis der Bellschen Ungleichung beruht, bezeichnet. Eine solche Abweichung ist beispielsweise, dass die Detektoren nicht alle Teilchen detektieren oder dass die Wahl der Messeinstellungen und die Messereignisse nicht raumartig voneinander getrennt sind (siehe auch den Abschnitt Schlupflöcher weiter unten). Im Jahr 2015 wurden die ersten als „schlupflochfrei“ bezeichneten Experimente publiziert.
Übersicht
Der Bell-Test hat seinen Ursprung in der Debatte zwischen Albert Einstein und anderen Pionieren der Quantenphysik, vor allem Niels Bohr. Einer der debattierten Aspekte der Theorie der Quantenmechanik war die Bedeutung der Heisenbergschen Unschärferelation. Diese besagt, dass es Eigenschaften gibt, deren genaue Kenntnis die genaue Kenntnis bestimmter anderer Eigenschaften desselben physikalischen Systems ausschließt. Nach der Unschärferelation können zum Beispiel Ort und Impuls eines Teilchens nicht gleichzeitig mit beliebig hoher Genauigkeit bestimmt werden.
1935 veröffentlichten Einstein, Boris Podolsky und Nathan Rosen einen Artikel,[1] in dem sie argumentierten, dass dies die Folge einer nur unvollständigen Beschreibung der Realität durch die Quantenmechanik sei. In einem Gedankenexperiment betrachteten sie dazu einen verschränkten Zustand zweier Teilchen, in dem die Summe der beiden Ortskoordinaten und die Differenz der beiden Impulse jeweils einen genauen Wert annehmen.[2] Wegen der strengen Korrelation zwischen beiden Systemen ließen sich nun durch Messung am zweiten Teilchen entweder Ort oder Impuls des ersten Teilchens genau bestimmen. Das ist gemäß der Quantenmechanik selbst dann möglich, wenn die beiden Teilchen sehr weit voneinander entfernt sind. Einstein und Koautoren sahen hier ein Paradoxon, das nach den drei Autoren als „EPR-Paradoxon“ bekannt wurde. Es ergibt sich, wenn man einerseits annimmt, dass sichere Vorhersagen der Theorie (wie zum Beispiel die des Impulses von Teilchen 1 nach einer Impulsmessung am Teilchen 2) ein „Element der Realität“ darstellen und andererseits Elemente der Realität nicht mit Überlichtgeschwindigkeit verändert oder beeinflusst werden können. Denn je nach Messung am Teilchen 2 erfüllt dann entweder der Wert des Orts oder der des Impulses von Teilchen 1 die von EPR an ein „Element der Realität“ gestellten Forderungen, und das unabhängig davon, wie weit die beiden Teilchen voneinander entfernt sind. Die drei Autoren schlossen daraus, dass die Quantenmechanik nicht vollständig sein könne und dass es eine ihr zugrundeliegende genauere Theorie geben müsse, die alle Elemente der Realität repräsentiere und unter Einhaltung des Lokalitätsprinzips die Vorhersagen der Quantenmechanik statistisch reproduziere. Solche Modelle werden als Lokale-Verborgene-Variablen-Modelle (LVV) bezeichnet.
In einer Theorie der verborgenen Variablen, wie Einstein sie sich vorstellte, wären die Zufälligkeit und Unbestimmtheit, die im Verhalten der Quantenteilchen zu beobachten sind, nur scheinbar. Wenn man zum Beispiel die Details aller verborgenen Variablen eines Teilchens kennen würde, könnte man sowohl seine Position als auch seinen Impuls vorhersagen. Die Unschärfe, die durch das Heisenbergsche Prinzip quantifiziert wird, wäre lediglich ein Artefakt, das sich daraus ergibt, dass man keine vollständigen Informationen über die verborgenen Variablen hat. Außerdem argumentierte Einstein, dass die verborgenen Variablen der Bedingung der Lokalität gehorchen sollten: Unabhängig davon, wie die verborgenen Variablen tatsächlich beschaffen sind, sollte ihr Verhalten für ein Teilchen das Verhalten der Variablen für ein anderes, weit entferntes Teilchen nicht unmittelbar beeinflussen können. Diese Idee, das so genannte Lokalitätsprinzip, beruht auf einer Grundlage der relativistischen Physik, dass sich Wechselwirkungen nicht schneller als mit Lichtgeschwindigkeit im Raum ausbreiten. Diese Ideen waren Gegenstand ständiger Debatten zwischen ihren Befürwortern. Insbesondere war Einstein selbst mit der Art und Weise, wie Podolsky das Problem in der berühmten EPR-Arbeit dargelegt hatte, nicht einverstanden.[3][4]
1964 stellte John Stewart Bell sein heute berühmtes Theorem auf, dass keine physikalische Theorie mit verborgenen lokalen Variablen jemals alle Vorhersagen der Quantenmechanik reproduzieren kann. Das Theorem impliziert die Aussage, dass der Determinismus der klassischen Physik grundsätzlich nicht in der Lage ist, die Quantenmechanik zu beschreiben. In Folgearbeiten erweiterte Bell das Theorem und schuf die konzeptionelle Grundlage für die Bell-Test-Experimente.
Bei einem typischen solchen Experiment werden Teilchenpaare, häufig Photonen, in einem verschränkten Zustand erzeugt und je eines der Teilchen zu einem von zwei voneinander entfernten Detektoren gesendet, mit denen bestimmte Eigenschaften der Teilchen, z. B. ihr Spin, gemessen werden. Um die beiden Detektoren voneinander zu unterscheiden, bezeichnet man sie oft in Anlehnung an Alice und Bob mit A und B. Der Zustand des Teilchenpaars und die Messungen sind so gewählt, dass Quantenmechanik und Lokaler Realismus verschiedene Vorhersagen machen. Die Ergebnisse des Experiments können dann mit den Vorhersagen des lokalen Realismus und den Vorhersagen der Quantenmechanik verglichen werden, um eine der beiden Beschreibungsweisen zu falsifizieren.
Theoretisch könnten die erhaltenen Ergebnisse „zufällig“ mit beiden Modellen vereinbar sein (da in beiden Modellen statistische Schwankungen auftreten und nicht unendlich viele Messungen gemacht werden können). Um dieses Problem zu lösen, schlug Bell eine mathematische Beschreibung des lokalen Realismus vor, die eine statistische Grenze für die Wahrscheinlichkeit dieser Eventualität setzt. Wenn die Ergebnisse eines Experiments gegen die Bellsche Ungleichung verstoßen, können lokale versteckte Variablen als Ursache mit zunehmender Gewissheit ausgeschlossen werden, je mehr Messungen eine Verletzung dieser Ungleichung zeigen. Spätere Forscher bauten auf Bells Arbeit auf, indem sie neue Ungleichungen vorschlugen, die demselben Zweck dienen und die Grundidee auf die eine oder andere Weise verfeinern.[5][6][7][8] Folglich kann der Begriff „Bell-Ungleichung“ eine beliebige von mehreren Ungleichungen bezeichnen, die von allen Theorien lokaler verborgener Variablen erfüllt werden. In der Praxis verwenden viele heutige Experimente die CHSH-Ungleichung (nach John Clauser, Michael Horne, Abner Shimony und Richard Holt). Alle diese Ungleichungen, wie auch die ursprüngliche von Bell entwickelte, bringen die Idee zum Ausdruck, dass die Annahme eines lokalen Realismus die statistischen Ergebnisse von Experimenten an Teilchenmengen, die an einer Wechselwirkung teilgenommen haben und dann getrennt wurden, einschränkt.
Bislang haben alle Bell-Tests die Theorie der Quantenphysik gestützt und nicht die Hypothese der lokalen verborgenen Variablen.
Optische Bell-Test-Experimente
In der Praxis wurde in den meisten bisher durchgeführten Experimenten Licht verwendet, das in Form von teilchenförmigen Photonen (erzeugt durch eine Atomkaskade oder durch spontane parametrische Abkonversion) emittiert wurde, und nicht, wie es Bell ursprünglich im Sinn hatte, Atome. Die interessierende Eigenschaft ist in den bekanntesten Experimenten die Polarisationsrichtung, obwohl auch andere Eigenschaften verwendet werden können. Solche Experimente lassen sich in zwei Klassen einteilen, je nachdem, ob die verwendeten Analysatoren einen oder zwei Ausgangskanäle haben.
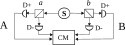
Ein typisches Zwei-Kanal (CHSH) Experiment

Das Diagramm zeigt ein typisches optisches Experiment mit zwei Kanälen wie das von Alain Aspect aus dem Jahr 1982.[9] Koinzidenzen (gleichzeitige Detektion von je einem Photon am Detektor bei A und bei B) werden aufgezeichnet, wobei die Ergebnisse als „++“, „+−“, „−+“ oder „−−“ kategorisiert und die entsprechenden Zählungen kumuliert werden. Damit kann eine Verletzung der CHSH-Ungleichung nachgewiesen werden.
Es werden vier getrennte Unterversuche durchgeführt, je einer für die vier Einstellungen der beiden Detektoren. Für den Detektor bei A werden die Einstellungen und verwendet und für den bei B und . Diese werden in der Regel so gewählt, dass den Winkeln 0, 45°, 22,5° bzw. 67,5° entsprechen. Diese „Bell-Test-Winkel“ sind diejenigen, für die die quantenmechanische Formel die größte Verletzung der CHSH-Ungleichung ergibt.
Für jede der vier Einstellungen werden der folgende Ausdruck aus den Koinzidenzzahlen gebildet:
Aus diesen experimentellen Werten lässt sich dann eine Abschätzung der Teststatistik S bestimmen
Wenn betragsmäßig größer als 2 ist, ist die CHSH-Ungleichung verletzt. Damit falsifiziert das Experiment alle lokalen Verborgene-Variablen-Modelle. Die quantenmechanische Vorhersage ist (für Photonen im für die Verletzung dieser Ungleichung optimalen, maximal verschränkten Bell-Zustand) ist .
In der Praxis werden in Experimenten mit Photonen nicht alle in der Quelle erzeugten Photonenpaare auch detektiert. Das verletzt eine der Annahmen, unter denen die CHSH-Ungleichung abgeleitet wurde. Damit verwendet werden kann, um lokalen Realismus auszuschließen, muss entweder der Anteil der nicht-detektierten Photonen sehr klein sein oder man muss zusätzlich annehmen, dass die Stichprobe der nachgewiesenen Paare repräsentativ für die von der Quelle ausgesandten Paare ist. Dass diese Annahme möglicherweise nicht zutrifft, ist das fair-sampling-Schlupfloch, das erst 2015 nach über 40 Jahren Bell-Tests geschlossen werden konnte.
Ein typisches CH74 (Ein-Kanal-) Experiment

Vor 1982 nutzten alle realisierten Bell-Tests „Ein-Kanal“-Setups und Variationen der für diesen Fall abgeleiteten Ungleichung, die in dem vielzitierten Artikel von Clauser, Horne, Shimony und Holt von 1969 als die geeignetste für den praktischen Gebrauch genannt wird.[5] Wie beim CHSH-Test gibt es vier „Teilexperimente“, in welchen jeder der zwei Polarisationsfilter eine von zwei möglichen Einstellungen hat. Aber es werden zusätzlich Experimente durchgeführt, in denen je einer der Filter oder beide fehlen. Für all diese Einstellungen werden Koinzidenzen gezählt und für die Teststatistik verwendet.
wobei das Symbol für das Fehlen des Polarisationsfilters steht.
Wenn größer ist als 0, sagt man, dass das Experiment die Bellsche Ungleichung verletzt und daher „den lokalen Realismus widerlegt“ habe. Um die Ungleichung auf Experimente mit Photonen anwendbar zu machen, mussten CHSH in ihrer Arbeit von 1969 eine zusätzliche Annahme treffen, die sogenannte „fair Sampling“-Annahme, dass die Wahrscheinlichkeit der Erkennung eines bestimmten Photons, sobald es den Polarisator passiert hat, unabhängig von der Polarisatoreinstellung (einschließlich der Einstellung „Abwesenheit“) ist. Wenn diese Annahme verletzt würde, könnte ein LVV-Modell im Prinzip die CHSH-Ungleichung verletzen. Diese Annahme war 1969 (und für Jahrzehnte danach) in der Praxis nötig, da Photonendetektoren oft nur einen sehr kleinen Anteil der emittierten Photonen detektierten und man annehmen musste, dass die detektierte Untermenge nicht speziell ausgewählt wurde, um die CHSH-Ungleichung zu verletzen. Wenn man das berücksichtigt, lässt sich zeigen, dass für Detektionswahrscheinlichkeiten unterhalb von 83 % kein Widerspruch mehr zwischen Quantenmechanik und lokalem Realismus vorliegt.[10]
In einem späteren Artikel aus dem Jahr 1974 ersetzten Clauser und Horne diese Annahme durch die schwächere Annahme „keine Verbesserung“ und leiteten eine modifizierte Ungleichung ab, die das mögliche Resultat „keine Detektion“ enthält (jetzt gibt es auf jeder Seite und bei jeder Detektoreinstellung drei mögliche Resultate) und nun für alle Detektoreffizienzen gilt. Eine Verletzung der Ungleichung durch die Quantenmechanik setzt eine Effizienz von mindestens 2/3 voraus.[11][10]
Annahmen über das Experiment und Schlupflöcher
Damit ein Experiment ein Bell-Test sein kann, ist es entscheidend, dass die mathematischen Annahmen, auf denen die Ableitung der Bellschen Ungleichung beruht, durch den experimentellen Aufbau garantiert sind. Das heißt konkret, dass die beiden Messungen raumartig voneinander getrennt sind, sodass sie sich nicht gegenseitig beeinflussen können, und dass die Wahl der Einstellungen beider Detektoren unabhängig voneinander und unabhängig von der Zustandspräparation erfolgt. Weiterhin wird üblicherweise in der Ableitung der Bellschen Ungleichung angenommen, dass die Messungen zweiwertige (dichotome) Observable realisieren, und also immer entweder den einen oder den anderen von zwei Messwerten liefern. Das beinhaltet insbesondere, dass sie alle detektiert werden. Es gibt aber auch Bell-Ungleichungen ohne diese Annahme.
In den tatsächlich durchgeführten Experimenten waren diese Voraussetzung nicht immer alle sichergestellt. Man spricht dann von „Schlupflöchern“ (engl. loopholes), die eine hypothetische lokal-realistische Theorie ausnutzen könnte, um die experimentellen Ergebnisse zu reproduzieren. Die drei in der Entwicklung der Bell-Tests wichtigsten Schlupflöcher sind die folgenden:[10][12]
- Das „Lokalitätsschlupfloch“ besteht, wenn die beiden Detektionsereignisse nicht raumartig getrennt sind. Um es zu schließen, wurde die räumliche Entfernung zwischen den Detektoren vergrößert und die Dauer der Messung reduziert.
- Das „Fair-Sampling-Schlupfloch“ (manchmal auch: Detektionsschlupfloch) betrifft nicht alle Bell-Tests, sondern nur solche, die Ungleichungen wie die CHSH-Ungleichung verwenden und bei denen ein wesentlicher Anteil der präparierten Systeme (Photonen) gar nicht detektiert wird. Man zieht dann bei der Berechnung der Korrelationen nur die Durchgänge des Experiments heran, bei denen an beiden Detektoren ein Photon gemessen wurde. Um auch in diesem Fall einen Widerspruch zum lokalen Realismus zu erhalten, muss zusätzlich angenommen werden, dass die durch die Koinzidenzen ausgewählte Teilmenge aller präparierten Systeme eine repräsentative („faire“) Auswahl darstellt.
- Das „Wahlfreiheitsschlupfloch“ besteht, wenn nicht garantiert ist, dass die Detektoreinstellungen statistisch unabhängig von den verborgenen Variablen erfolgt, d. h. von der Präparation des Anfangszustands des zu messenden Systems. Streng logisch kann dieses Schlupfloch nicht geschlossen werden, da lokal-realistische Modelle denkbar sind, in denen die Detektoreinstellungen in allen Bell-Tests schon von Anfang an so festgelegt sind, dass die Bellungleichungen verletzt werden. Wegen dieses Extrembeispiels spricht man bei Modellen, die dieses Schlupfloch ausnutzen, oft von Superdeterminismus, obwohl gezeigt wurde, dass zur Verletzung der Bellschen Ungleichung schon eine schwache Korrelation zwischen den verborgenen Variablen der Teilchen und den Detektoreinstellungen genügt.[12] Der Name rührt daher, dass es geschlossen wäre, wenn die Experimentatoren die Detektoreistellungen (unabhängig von allen verborgenen Parametern der Teilchen) frei wählen könnten.
In manchen Experimenten lagen noch andere Schlupflöcher vor.[10] Im Laufe von fast 50 Jahren seit 1972 wurden die Schlupflöcher geschlossen bzw. immer weiter verengt, aber bis 2015 konnten die Ergebnisse aller Experimente, die eine Bell-Ungleichung verletzten, theoretisch immer noch durch hypothetische lokal-realistische Modelle erklärt werden, die das Lokalitäts- oder das Fair-Sampling-Schlupfloch ausnützten.
Im Jahr 2015 wurde dann erstmals Bell-Verletzungen publiziert, bei der beide Schlupflöcher gleichzeitig geschlossen waren.[13][14] Das erste dieser Experimente nutzte die verschränkten Spins von zwei Fehlstellen in Diamanten in zwei 1,3 km voneinander entfernten Labors,[15] die beiden kurz darauf zeitgleich veröffentlichten Experimente verwendeten verschränkte Photonen und erreichten eine viel größere statistischen Signifikanz.[16][17]
Die verbleibenden möglichen Theorien, die dem lokalen Realismus gehorchen, können durch verfeinerte Experimente weiter eingeschränkt werden. In der Hauptsache geht es dabei um das Wahlfreiheitsschlupfloch. Um es auszunutzen, müssen lokal-realistische Theorien eine Abhängigkeit der Detektoreinstellungen von den verborgenen Variablen beschreiben. Indem man die Detektoreinstellung von anderen, mit den verschränkten Teilchen augenscheinlich nicht in Zusammenhang stehenden physikalischen Prozessen abhängig macht, kann man die Anforderungen, die eine solche Theorie erfüllen müsste, erhöhen. Vorgeschlagen und umgesetzt wurden hier einerseits Vorschläge, die Einstellungen vom Zustand von Photonen abhängig zu machen, die von fernen astronomischen Objekten ausgesandt wurden[18] und andererseits die Verwendung von Menschen zur Generierung der Messeinstellungen.[19]
Trotz aller Mängel der realisierten Experimente zeigt sich eine bemerkenswerte Tatsache: Die Ergebnisse entsprechen alle in sehr guter Näherung den Vorhersagen der Quantenmechanik. Wenn unvollkommene Experimente eine so hervorragende Übereinstimmung mit Quantenvorhersagen liefern, stimmen die meisten praktizierenden Quantenphysiker mit John Bell darin überein, dass die Bell-Ungleichungen auch dann verletzt würden, wenn ein perfekter Bell-Test durchgeführt würde. Diese Haltung hat zur Entstehung eines neuen Teilgebiets der Physik geführt, das heute als Quanteninformationstheorie bekannt ist.[20] Eine der wichtigsten Errungenschaften dieses neuen Zweigs der Physik ist der Nachweis, dass die Verletzung der Bellschen Ungleichungen zur Möglichkeit für eine quantitativ überprüfbar abhörsichere Informationsübertragung führt (Quantenkryptographie). Dieser Zusammenhang wurde erstmals 1991 von Artur Ekert in seinem Vorschlag für ein Verfahren zum Quantenschlüsselaustausch hergestellt und ist heute zentral für das Konzept der geräteunabhängigen Sicherheit (device-independent security) von Quantenkommunikationssystemen.[21]
Auswahl bedeutsamer Experimente
Im Laufe der letzten knapp fünfzig Jahre wurde eine große Anzahl von Bell-Tests durchgeführt.[22] Die Ergebnisse dieser Experimente bestätigten die Vorhersagen der Quantenmechanik und waren mit Modellen lokaler verborgener Variablen nur Ausnutzung verschiedener Schlupflöcher kompatibel und werden daher üblicherweise dahingehend interpretiert, dass sie lokale verborgene Variablen ausschließen bzw. unplausibel machen. Die ersten Experimente, die gleichzeitig das Lokalitäts- und das Fair-Sampling-Schlupfloch schließen, wurden 2015 veröffentlicht.[15][16][17] Ein Experiment ist frei vom Lokalitätsschlupfloch, wenn für jede Messung die Wahl und Einstellung des Detektorsettings in jedem Arm des Experiments raumartig getrennt sind von der Messung im anderen Arm, das heißt, wenn das Setting in einem Arm das Messergebnis im anderen nach der speziellen Relativitätstheorie nicht beeinflussen kann. Ein Experiment schließt das Fair-Sampling-Schlupfloch, wenn ein hinreichend großer Anteil der Experimente zu Messergebnissen in beiden Armen des Experiments führt.[23][24]
Zu den bekanntesten und neuesten Experimenten zählen:
Freedman und Clauser (1972)
Stuart J. Freedman und John Clauser waren die ersten, die einen Bell-Test ausführten. Sie benutzten Freedmans Ungleichung, eine Variante der CH74-Ungleichung.[25] John Clauser erhielt 2022 für diese Arbeiten den Nobelpreis für Physik.[26]
Aspect et al. (1982)
Alain Aspect und sein Team in Orsay bei Paris, führten drei Bell-Test-Experimente durch, in denen sie eine Zwei-Photonen-Kaskade in Kalziumatomen als Quelle verschränkter Photonen verwendeten. Das erste und dritte ihrer Experimente nutze ebenfalls die CH74-Ungleichung, während das zweite die CHSH-Ungleichung verwendete. Im dritten (und bekanntesten) der Experimente erfolgte die Einstellung der Detektoren während sich die Photonen schon auf dem Weg zu den Detektoren befanden.[27][28] Alain Aspect erhielt 2022 für diese Arbeiten den Nobelpreis für Physik.[29]
Tittel et al. (1998)
Die Genfer Bell-Test-Experimente zeigten, dass Verschränkung auch über große Distanzen erhalten bleiben kann. Es wurde Licht durch Glasfaserkabel über Distanzen von einigen Kilometern übertragen, bevor es gemessen wurde. Wie in fast allen Bell-Experimenten seit 1985 wurde der Prozess der parametrischen Abkonversion (englisch: parametric down-conversion (PDC)) als Quelle verschränkter Photonen verwendet.[30][31]
Weihs et al. (1998): Experiment unter strengen Einstein-Lokalitäts-Bedingungen
Gregor Weihs und ein Team unter der Führung von Anton Zeilinger führten an der Universität Innsbruck ein Experiment durch, welches das Lokalitätsschlupfloch in einer gegenüber dem Aspect-Experiment verbesserten Weise schloss, indem die Detektorstellung durch einen physikalischen, auf einer Quantenmessung beruhenden Zufallsgenerator festgelegt wurde (statt durch einen Pseudozufallszahlengenerator). In diesem Test wurde die CHSH-Ungleichung um über 30 Standardabweichungen verletzt und stimmten mit den Vorhersagen der Quantentheorie überein.[32]
Pan et al. (2000) Experiment mit dem GHZ-Zustand
Dieses an der Universität Wien durchgeführte Experiment ist das erste einer neuen Klasse von Bell-Test-artigen Experimenten, die LVV-Modelle, in einem Setting von mehr als zwei Parteien testen. Konkret wurde ein GHZ-Experiment durchgeführt, das den sogenannten Greenberger-Horne-Zeilinger-Zustand-Zustand von drei Photonen verwendet.[33]
Rowe et al. (2001): erster Bell-Test ohne Detektionsschlupfloch
Das Detektionsschlupfloch wurde erstmals in einem Bell-Experiment mit zwei verschränkten Ionen in einer Ionenfalle in der Gruppe von David Wineland am National Institute of Standards and Technology in Boulder (Colorado) geschlossen. Dies war dank Detektionseffizienzen von weit über 90 % möglich. Allerdings war keine raumartige Trennung von Detektorsetting und Detektion gegeben.[34]
Gröblacher et al. (2007) Test nicht-lokaler realistischer Theorien vom Leggett-Typ
Eine spezielle Klasse nicht-lokaler realistischer Theorien, die von Anthony Leggett vorgeschlagen worden war, wurde durch dieses Experiment an der Universität Wien ausgeschlossen. Die Autoren ziehen den Schluss, dass selbst wenn man Nicht-Lokalität zulässt, jedes Verborgene-Variablen-Modell, das mit der Quantenmechanik konsistent ist, hochgradig kontraintuitiv sein muss.[35][36]
Salart et al. (2008): Große Entfernung zwischen den Detektoren
In diesem Experiment an der Universität Genf waren die Detektoren 18 km voneinander entfernt, der bis dahin größte in einem Bell-Test erreichte Abstand. Diese Distanz stellte sicher, dass die Quantenmessungen abgeschlossen waren, bevor ein Signal von einem Detektor den anderen hätte erreichen können.[37][38]
Ansmann et al. (2009): Festkörperbasierte Qubits ohne Detektionsschlupfloch
In diesem Experiment an der University of California, Santa Barbara wurden mit Supraleitern und Josephson-Kontakten realisierte Phasenqubits verwendet und damit erstmals ein Bell-Test in einem Festkörpersystem durchgeführt. Da sowohl die Erzeugung des verschränkten Zustands als auch die Bell-Messung mit 100 % Effizienz erfolgten, bestand kein Detektionsschlupfloch. Da die Qubits aber nur wenige Millimeter voneinander entfernt waren, bestand das Lokalitätsschlupfloch. Die CHSH-Ungleichung wurde um 244 Standardabweichungen verletzt.[39]
Giustina et al. (2013): Schließen des Detektionsschlupflochs für Photonen
Für Photonen wurde das Detektionsschlupfloch erstmal mit einem Experiment der Gruppe von Anton Zeilinger geschlossen, das hocheffiziente supraleitende transition-edge Sensoren verwendete. Damit waren Photonen das erste System, in dem alle wesentliche Schlupflöcher geschlossen werden konnten (allerdings in verschiedenen Experimenten).[40]
Das mit einer kontinuierlichen Photonenquelle und nur viermal geänderten Messeinstellungen arbeitende Experiment schien zunächst dem Koinzidenzschlupfloch zu unterliegen. Eine genauere Analyse der Daten zeigte jedoch, dass dies nicht der Fall war.[41] Ein fast zeitgleiches Experiment in der Gruppe von Nicolas Gisin, gepulst und mit oft und zufällig veränderten Messeinstellungen, schloss ebenfalls das Detektionsschlupfloch und war vom Koinzidenzschlupfloch nicht betroffen.[42]
Hensen et al., Giustina et al. und Shalm et al. (2015): Erste „schlupflochfreie“ Bell-Tests
Im Jahr 2015 wurden innerhalb von drei Monaten von drei unabhängigen Forschergruppen in Delft, Wien und Boulder schlupflochfreie Bell-Tests publiziert.[43] Alle drei Tests schlossen sowohl das Detektions- als auch das Lokalitätsschlupfloch (und das Gedächtnisschlupfloch). Sie gelten als schlupflochfrei, da die verbleibenden Schlupflöcher (wie z. B. der „Superdeterminismus“) auf sehr exotischen Annahmen beruhen und sich der experimentellen Überprüfung entziehen.
Das zuerst veröffentlichte Experiment von Hensen et al.[15] an der TU Delft benutzte Photonen, um den Spin von zwei Stickstoff-Fehlstellen-Zentren („NV-Zentren“) in zwei 1,3 km voneinander entfernten Diamanten zu verschränken und dann eine Verletzung der CHSH-Ungleichung () durch die Spins nachzuweisen. Damit widersprach es der lokal-realistischen Hypothese mit einem p-Wert von 0,039, d. h., die Wahrscheinlichkeit, das entsprechende Ergebnis in einer lokal-realistischen Welt zufällig zu messen, betrug nicht mehr als 3,9 %.[13]
Die beiden kurz darauf gleichzeitig veröffentlichten Experimente von Giustina et al.[16] und Shalm et al.[17] benutzten verschränkte Photonen und wiesen eine Bell-Verletzung mit hoher statistischer Signifikanz (p-Wert ) nach.
Schmied et al. (2016): Bell-Korrelationen in einem Vielteilchensystem
Mittels eines Verschränkungszeugen für Bell-Korrelationen, der von einer für viele Parteien (nicht nur, wie im Fall der CHSH-Ungleichung, für zwei) geltenden Bell-Ungleichung abgeleitet wurde, wurden in einem Experiment an der Universität Basel erstmals Bell-Korrelationen in einem Vielteilchensystem, konkret ca. 480 kalte Atome in einem Bose-Einstein-Kondensat, nachgewiesen. Zwar waren die üblichen Schlupflöcher hier nicht geschlossen, aber das Experiment zeigt, dass Bell-Korelationen auch für Systeme großer Teilchenzahl messbar sind.[44]
Handsteiner et al. (2017): „Kosmischer Bell-Test“ – Messeinstellungen durch Sternenlicht
Das Experiment unter der Leitung von David Kaiser (MIT) und Anton Zeilinger (IQOQI und Universität Wien) zielt auf das freedom of choice-Schlupfloch. Es geht auf einen Vorschlag von Kaiser zurück.[45] Dazu wurden die Messeinstellungen der beiden Detektoren durch Quantenmessungen an Photonen bestimmt, die von zwei verschiedenen und voneinander weit entfernten Sternen der Milchstraße stammten. Dadurch wurde sichergestellt, dass alle denkbaren kausalen Einflüsse, die das Schlupfloch ausnützen könnten (indem die Messeinstellungen nicht unabhängig von den Werten der verborgenen Variablen der verschränkten Photonen sind), mindestens über 570 Jahre in der Vergangenheit liegen müssten.[46] Das Experiment „stellt das erste Experiment dar, das den Raum-Zeit-Bereich, in dem verborgene Variablen relevant sein könnten, drastisch einschränkt“.[47][48]
Rosenfeld et al. (2017): Bell-Test mit verschränkten Atomen und ohne Detektions- und Lokalitätsschlupfloch
In einem Experiment an der Ludwig-Maximilians-Universität München und dem Max-Planck-Institut für Quantenoptik wurde eine Bell-Ungleichung bei Messungen an verschränkten atomaren Spins in zwei 398 m voneinander entfernten Laboren verletzt. Der verschränkte Zustand wird erzeugt, indem zunächst zwei gefangene Atome mit je einem Photon verschränkt werden und die Verschränkung dann mittels einer gemeinsamen Messung der Photonen auf die Atome übertragen wird (entanglement swapping). Die Erzeugung des verschränkten Zustands wird also durch das photonische Messergebnis „angekündigt“ (heralded entanglement) und es gibt daher kein fair sampling-Schlupfloch. Detektions-, Lokalitäts- und Gedächtnisschlupfloch waren geschlossen. Die beobachtete Bell-Verletzung von erlaubte, den lokalen Realismus mit einem p-Wert von 1,02 · 10−16 zu verwerfen, wofür die Daten von sieben Monaten und insgesamt 55.000 Messereignissen verwendet wurden.[49]
The BIG Bell Test Collaboration (2018): Den lokalen Realismus durch menschliche Entscheidungen herausfordern
Auch dieser Bell-Test war durch das freedom-of-choice-Schlupfloch motiviert. In Zusammenarbeit von zwölf Laboren auf fünf Kontinenten wurden insgesamt 13 Bell-Experimente (auf verschiedenen Plattformen) durchgeführt, wobei die Messeinstellungen von den Entscheidungen mehrerer 10.000 Teilnehmer an einem dafür designten Onlinespiel bestimmt wurden. Die Experimente waren konsistent mit den Vorhersagen der Quantenmechanik und verletzten die getesteten Bell-Ungleichungen um mehrere (3) bis viele (>100) Standardabweichungen. Um dieses Ergebnis lokal-realistisch zu erklären, müssten verborgene Variablen die Entscheidungen der Teilnehmer geeignet miteinander korreliert haben.[50]
Rauch et al (2018): Messeinstellung bestimmt durch Quasare
In diesem Experiment[51] wird der letztmögliche Zeitpunkt, zu dem lokal-realistische verborgene Variablen das freedom-of-choice-Schlupfloch ausgenutzt haben könnten auf mehr als 7,8 Milliarden Jahre in die Vergangenheit geschoben, da die Messeinstellungen des Bell-Tests durch das Licht zweier weit entfernter Quasare bestimmt wurde. Mehr als 95 % des Raumzeitvolumens in unserem Rückwärts-Lichtkegel werden dadurch als Quelle dieser Beeinflussung ausgeschlossen.[52][53]
Die 2019 ausgestrahlte Episode Einstein's Quantum Riddle von PBS Nova dokumentiert diesen „kosmischen Bell-Test“ mit Aufnahmen des Forscherteams im Teide Observatorium auf den Kanarischen Inseln.[54]
Einzelnachweise
- ↑ A. Einstein, N. Podolsky, E. Rosen: Can Quantum Mechanical Description of Physical reality be considered complete? In: Phys. Rev. Band 47, 1935, S. 777, doi:10.1103/PhysRev.47.777.
- ↑ Ein solcher Zustand ist mit der Unschärferelation kompatibel, da und miteinander kommutieren.
- ↑ Arthur Fine: The Shaky Game: Einstein, Realism, and the Quantum Theory. 2nd Auflage. University of Chicago Press, Chicago 1996 (englisch).
- ↑ Nicholas Harrigan, Robert W. Spekkens: Einstein, Incompleteness, and the Epistemic View of Quantum States. In: Foundations of Physics. 40. Jahrgang, Nr. 2, 1. Februar 2010, ISSN 0015-9018, S. 125–157, doi:10.1007/s10701-009-9347-0, arxiv:0706.2661, bibcode:2010FoPh...40..125H (englisch).
- ↑ a b John F. Clauser, Michael A. Horne, Abner Shimony, Richard A. Holt: Proposed Experiment to Test Local Hidden-Variable Theories. In: Physical Review Letters. 23. Jahrgang, Nr. 15, 13. Oktober 1969, S. 880–884, doi:10.1103/PhysRevLett.23.880, bibcode:1969PhRvL..23..880C (englisch).
- ↑ Samuel L. Braunstein, Carlton M. Caves: Information-Theoretic Bell Inequalities. In: Physical Review Letters. 61. Jahrgang, Nr. 6, 1988, S. 662–665, doi:10.1103/physrevlett.61.662, PMID 10039398, bibcode:1988PhRvL..61..662B (englisch).
- ↑ Richard D. Gill: Time, Finite Statistics, and Bell's Fifth Position (= Foundations of Probability and Physics - 2). Växjö University Press, 2003, S. 179–206, arxiv:quant-ph/0301059 (englisch).
- ↑ David Elkouss, Stephanie Wehner: (Nearly) optimal P-values for all Bell inequalities. In: npj Quantum Information. Band 2, 2016, S. 16026, doi:10.1038/npjqi.2016.26, arxiv:1510.07233 (englisch).
- ↑ Alain Aspect, Philippe Grangier, Gérard Roger: Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell's Inequalities. In: Phys. Rev. Lett. 49. Jahrgang, Nr. 2, 1982, S. 91–94, doi:10.1103/PhysRevLett.49.91, bibcode:1982PhRvL..49...91A (englisch).
- ↑ a b c d J. Kofler: Endspiel für den lokalen Realismus. In: Physik in unserer Zeit. Band 46, 2015, S. 288–295, doi:10.1002/piuz.201501412.
- ↑ J. F. Clauser, M. A. Horne: Experimental consequences of objective local theories. In: Phys. Rev. D. 10. Jahrgang, Nr. 2, 1974, S. 526–35, doi:10.1103/PhysRevD.10.526 (englisch).
- ↑ a b David I. Kaiser: Tackling Loopholes in Experimental Tests of Bell’s Inequality. In: Olival Freire (Hrsg.): The Oxford Handbook of the History of Quantum Interpretations. Oxford Academic, 2022, Kap. 13, S. 339–370, doi:10.1093/oxfordhb/9780198844495.013.0014, arxiv:2011.09296.
- ↑ a b Rainer Scharf: Bell-Test ohne Schlupfloch. In: pro-physik.de. 21. Oktober 2015, abgerufen am 13. Oktober 2023.
- ↑ H. Wiseman: Quantum physics: Death by experiment for local realism. In: Nature. 526. Jahrgang, Nr. 7575, 21. Oktober 2015, S. 649–650, doi:10.1038/nature15631 (englisch).
- ↑ a b c Hensen: Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. In: Nature. 526. Jahrgang, Nr. 7575, 2015, S. 682–686, doi:10.1038/nature15759, PMID 26503041, arxiv:1508.05949, bibcode:2015Natur.526..682H (englisch).
- ↑ a b c Marissa Giustina, Marijn A. M. Versteegh, Soeren Wengerowsky, Johannes Handsteiner, Armin Hochrainer, Kevin Phelan, Fabian Steinlechner, Johannes Kofler, Jan-Ake Larsson, Carlos Abellan, Waldimar Amaya, Valerio Pruneri, Morgan W. Mitchell, Joern Beyer, Thomas Gerrits, Adriana E. Lita, Lynden K. Shalm, Sae Woo Nam, Thomas Scheidl, Rupert Ursin, Bernhard Wittmann, Anton Zeilinger: A significant-loophole-free test of Bell's theorem with entangled photons. In: Physical Review Letters. 115. Jahrgang, Nr. 25, 2015, S. 250401, doi:10.1103/PhysRevLett.115.250401, PMID 26722905, arxiv:1511.03190, bibcode:2015PhRvL.115y0401G (englisch).
- ↑ a b c Lynden K. Shalm, Evan Meyer-Scott, Bradley G. Christensen, Peter Bierhorst, Michael A. Wayne, Martin J. Stevens, Thomas Gerrits, Scott Glancy, Deny R. Hamel, Michael S. Allman, Kevin J. Coakley, Shellee D. Dyer, Carson Hodge, Adriana E. Lita, Varun B. Verma, Camilla Lambrocco, Edward Tortorici, Alan L. Migdall, Yanbao Zhang, Daniel R. Kumor, William H. Farr, Francesco Marsili, Matthew D. Shaw, Jeffrey A. Stern, Carlos Abellán, Waldimar Amaya, Valerio Pruneri, Thomas Jennewein, Morgan W. Mitchell, Paul G. Kwiat, Joshua C. Bienfang, Richard P. Mirin, Emanuel Knill, Sae Woo Nam: A strong loophole-free test of local realism. In: Phys Rev Lett. 115. Jahrgang, Nr. 25, 2015, S. 250402, doi:10.1103/PhysRevLett.115.250402, PMID 26722906, PMC 5815856 (freier Volltext), arxiv:1511.03189, bibcode:2015PhRvL.115y0402S (englisch).
- ↑ J. Gallicchio, A. S. Friedman, D. I. Kaiser: Testing Bell’s Inequality with Cosmic Photons: Closing the Setting-Independence Loophole. In: Phys. Rev. Lett. Band 112, 2014, S. 110405, doi:10.1103/PhysRevLett.112.110405, arxiv:1310.3288.
- ↑ H. Wiseman: Quantum physics: Death by experiment for local realism. In: Nature. 526. Jahrgang, Nr. 7575, 21. Oktober 2015, S. 649–650, doi:10.1038/nature15631 (englisch).
- ↑ I. Georgescu: How the Bell tests changed quantum physics. In: Nat Rev Phys. Band 3, 2021, S. 674–676, doi:10.1038/s42254-021-00365-8.
- ↑ V. Zapatero, T. van Leent, R. Arnon-Friedman et al.: Advances in device-independent quantum key distribution. In: npj Quantum Inf. Band 9, 2023, S. 10, doi:10.1038/s41534-023-00684-x.
- ↑ Für eine Kurzübersicht und weiterführende Referenzen zu frühen Bell-Tests, siehe z. B. Wayne Myrvold, Marco Genovese, Abner Shimony: Bell’s Theorem. In: The Stanford Encyclopedia of Philosophy. Edward N. Zalta, September 2021, abgerufen am 1. November 2023. Siehe auch die Artikel von Brunner et al und Bertlmann und Zeilinger aus der Literaturliste.
- ↑ Johannes Kofler: Endspiel für den lokalen Realismus. In: Physik in unserer Zeit. Band 46, Nr. 6, 2015, S. 288, doi:10.1002/piuz.201501412.
- ↑ Das Fair-Sampling-Schlupfloch ist vor allem für Photonenexperimente wichtig, da aufgrund von Verlusten und Detektorineffizienzen oft nur ein kleiner Teil der Photonen zu Detektionen führt. Für Bellsche Ungleichungen wie die CHSH-Ungleichung lassen sich bei zu niedriger Detektionseffizienz Lokale-Verborgene-Variablen-Modelle angeben, für die die detektierten Photonenpaare die Ungleichung verletzen. Das Schlupfloch lässt sich entweder über erhöhte Detektoreffizienz (>83 %) schließen oder durch die Verwendung einer Ungleichung, die ohne eine Fair-Sampling-Annahme abgeleitet wurde (z. B. die CH-Ungleichung). Solche Ungleichungen setzen aber in der Regel auch eine hohe Detektoreffizienz voraus.
- ↑ S.J. Freedman, J.F. Clauser: Experimental test of local hidden-variable theories. In: Phys. Rev. Lett. 28. Jahrgang, Nr. 938, 1972, S. 938–941, doi:10.1103/PhysRevLett.28.938, bibcode:1972PhRvL..28..938F (englisch, escholarship.org [PDF]).
- ↑ John Clauser: Facts. In: nobelprize.org. Abgerufen am 10. Oktober 2023 (englisch).
- ↑ Alain Aspect, Philippe Grangier, Gérard Roger: Experimental Tests of Realistic Local Theories via Bell's Theorem. In: Phys. Rev. Lett. 47. Jahrgang, Nr. 7, 1981, S. 460–3, doi:10.1103/PhysRevLett.47.460, bibcode:1981PhRvL..47..460A (englisch).
- ↑ Alain Aspect, Jean Dalibard, Gérard Roger: Experimental Test of Bell's Inequalities Using Time-Varying Analyzers. In: Phys. Rev. Lett. 49. Jahrgang, Nr. 25, 1982, S. 1804–7, doi:10.1103/PhysRevLett.49.1804, bibcode:1982PhRvL..49.1804A (englisch).
- ↑ Alain Aspect: Facts. In: nobelprize.org. Abgerufen am 10. Oktober 2023 (englisch).
- ↑ W. Tittel, J. Brendel, B. Gisin, T. Herzog, H. Zbinden, N. Gisin: Experimental demonstration of quantum-correlations over more than 10 kilometers. In: Physical Review A. 57. Jahrgang, Nr. 5, 1998, S. 3229–3232, doi:10.1103/PhysRevA.57.3229, arxiv:quant-ph/9707042, bibcode:1998PhRvA..57.3229T (englisch).
- ↑ W. Tittel, J. Brendel, H. Zbinden, N. Gisin: Violation of Bell inequalities by photons more than 10 km apart. In: Physical Review Letters. 81. Jahrgang, Nr. 17, 1998, S. 3563–6, doi:10.1103/PhysRevLett.81.3563, arxiv:quant-ph/9806043, bibcode:1998PhRvL..81.3563T (englisch).
- ↑ G. Weihs, T. Jennewein, C. Simon, H. Weinfurter, A. Zeilinger: Violation of Bell's inequality under strict Einstein locality conditions. In: Phys. Rev. Lett. 81. Jahrgang, Nr. 23, 1998, S. 5039–5043, doi:10.1103/PhysRevLett.81.5039, arxiv:quant-ph/9810080, bibcode:1998PhRvL..81.5039W (englisch).
- ↑ Jian-Wei Pan, D. Bouwmeester, M. Daniell, H. Weinfurter, A. Zeilinger: Experimental test of quantum nonlocality in three-photon GHZ entanglement. In: Nature. 403. Jahrgang, Nr. 6769, 2000, S. 515–519, doi:10.1038/35000514, PMID 10676953, bibcode:2000Natur.403..515P (englisch).
- ↑ M.A. Rowe, D. Kielpinski, V. Meyer, C.A. Sackett, W.M. Itano, C. Monroe, D.J. Wineland: Experimental violation of a Bell's inequality with efficient detection. In: Nature. 409. Jahrgang, Nr. 6822, 2001, S. 791–94, doi:10.1038/35057215, PMID 11236986, bibcode:2001Natur.409..791K (englisch, umich.edu [PDF]).
- ↑ Jon Cartwright: Quantum physics says goodbye to reality. physicsworld.com, 2007, archiviert vom am 19. Oktober 2007 (englisch).
- ↑ S Gröblacher, T Paterek, Rainer Kaltenbaek, C Brukner, M Zukowski, M Aspelmeyer, A Zeilinger: An experimental test of non-local realism. In: Nature. 446. Jahrgang, Nr. 7138, 2007, S. 871–5, doi:10.1038/nature05677, PMID 17443179, arxiv:0704.2529, bibcode:2007Natur.446..871G (englisch).
- ↑ Salart, D., Baas, A., van Houwelingen, J. A. W., N. Gisin, H. Zbinden: Spacelike Separation in a Bell Test Assuming Gravitationally Induced Collapses. In: Physical Review Letters. 100. Jahrgang, Nr. 22, 2008, S. 220404, doi:10.1103/PhysRevLett.100.220404, PMID 18643408, arxiv:0803.2425, bibcode:2008PhRvL.100v0404S (englisch).
- ↑ World's Largest Quantum Bell Test Spans Three Swiss Towns. phys.org, 16. Juni 2008 (englisch).
- ↑ Markus Ansmann, H. Wang, Radoslaw C. Bialczak, Max Hofheinz, Erik Lucero, M. Neeley, A. D. O’Connell, D. Sank, M. Weides, J. Wenner, A. N. Cleland, John M. Martinis: Violation of Bell's inequality in Josephson phase qubits. In: Nature. 461. Jahrgang, Nr. 504–6, 24. September 2009, S. 504–6, doi:10.1038/nature08363, PMID 19779447, bibcode:2009Natur.461..504A (englisch).
- ↑ Marissa Giustina, Alexandra Mech, Sven Ramelow, Bernhard Wittmann, Johannes Kofler, Jörn Beyer, Adriana Lita, Brice Calkins, Thomas Gerrits, Sae Woo Nam, Rupert Ursin, Anton Zeilinger: Bell violation using entangled photons without the fair-sampling assumption. In: Nature. 497. Jahrgang, Nr. 7448, 14. April 2013, S. 227–30, doi:10.1038/nature12012, PMID 23584590, arxiv:1212.0533, bibcode:2013Natur.497..227G (englisch).
- ↑ Jan-Åke Larsson, Marissa Giustina, Johannes Kofler, Bernhard Wittmann, Rupert Ursin, Sven Ramelow: Bell violation with entangled photons, free of the coincidence-time loophole. In: Physical Review A. 90. Jahrgang, Nr. 7448, 16. September 2014, S. 032107, doi:10.1103/PhysRevA.90.032107, arxiv:1309.0712, bibcode:2014PhRvA..90c2107L (englisch).
- ↑ B.G. Christensen, K. T. McCusker, J. Altepeter, B. Calkins, T. Gerrits, A. Lita, A. Miller, L. K. Shalm, Y. Zhang, S. W. Nam, N. Brunner, C. C. W. Lim, N. Gisin, P. G. Kwiat: Detection-Loophole-Free Test of Quantum Nonlocality, and Applications. In: Physical Review Letters. 111. Jahrgang, Nr. 7448, 26. September 2013, S. 130406, doi:10.1103/PhysRevLett.111.130406, PMID 24116754, arxiv:1306.5772, bibcode:2013PhRvL.111m0406C (englisch).
- ↑ Johanna L. Miller: Three groups close the loopholes in tests of Bell’s theorem. In: Physics Today. Band 69, Nr. 1, 2016, S. 14–16, doi:10.1063/PT.3.3039 (englisch).
- ↑ R. Schmied, J.-D. Bancal, B. Allard, M. Fadel, V. Scarani, P. Treutlein, N. Sangouard: Bell correlations in a Bose-Einstein condensate. In: Science. 352. Jahrgang, Nr. 6284, 2016, S. 441–4, doi:10.1126/science.aad8665, PMID 27102479, arxiv:1604.06419, bibcode:2016Sci...352..441S (englisch).
- ↑ Rainer Kayser: Kosmischer Test für die Quantenphysik. In: spektrum.de. 24. April 2014, abgerufen am 13. Oktober 2023.
- ↑ Johannes Handsteiner, Andrew S Friedman, Dominik Rauch, Jason Gallicchio, Bo Liu, Hannes Hosp, Johannes Kofler, David Bricher, Matthias Fink, Calvin Leung, Anthony Mark, Hien T Nguyen, Isabella Sanders, Fabian Steinlechner, Rupert Ursin, Sören Wengerowsky, Alan H Guth, David I Kaiser, Thomas Scheidl, Anton Zeilinger: Cosmic Bell Test: Measurement Settings from Milky Way Stars. In: Physical Review Letters. 118. Jahrgang, Nr. 6, 7. Februar 2017, S. 060401, doi:10.1103/PhysRevLett.118.060401, PMID 28234500, arxiv:1611.06985, bibcode:2017PhRvL.118f0401H (englisch).
- ↑ Natalie Wolchover: Experiment Reaffirms Quantum Weirdness. In: Quanta Magazine. 7. Februar 2017, abgerufen am 19. Juli 2023 (amerikanisches Englisch).
- ↑ Cosmic experiment is closing another Bell test loophole. In: Physics Today. 5. Jahrgang, 2016, doi:10.1063/pt.5.2051 (englisch).
- ↑ W. Rosenfeld, D. Burchardt, R. Garthoff, K. Redeker, N. Ortegel, M. Rau, H. Weinfurter: Event-Ready Bell Test Using Entangled Atoms Simultaneously Closing Detection and Locality Loopholes. In: Physical Review Letters. 119. Jahrgang, Nr. 1, 2017, S. 010402, doi:10.1103/PhysRevLett.119.010402, PMID 28731745, arxiv:1611.04604, bibcode:2017PhRvL.119a0402R (englisch).
- ↑ BIG Bell Test Collaboration: Challenging local realism with human choices. In: Nature. 557. Jahrgang, Nr. 7704, Mai 2018, ISSN 0028-0836, S. 212–216, doi:10.1038/s41586-018-0085-3, PMID 29743691, arxiv:1805.04431, bibcode:2018Natur.557..212B (englisch).
- ↑ Dominik Rauch, Johannes Handsteiner, Armin Hochrainer, Jason Gallicchio, Andrew S. Friedman, Calvin Leung, Bo Liu, Lukas Bulla, Sebastian Ecker, Fabian Steinlechner, Rupert Ursin, Beili Hu, David Leon, Chris Benn, Adriano Ghedina, Massimo Cecconi, Alan H. Guth, David I. Kaiser, Thomas Scheidl, Anton Zeilinger: Cosmic Bell Test Using Random Measurement Settings from High-Redshift Quasars. In: Physical Review Letters. 121. Jahrgang, Nr. 8, 20. August 2018, S. 080403, doi:10.1103/PhysRevLett.121.080403, PMID 30192604, arxiv:1808.05966 (englisch).
- ↑ Hamish Johnston: Cosmic Bell test uses light from ancient quasars, Physics World, 21. August 2018. Abgerufen am 22. Juli 2023 (englisch).
- ↑ Robert Gast: Spukhafte Fernwirkung ohne kosmische Verschwörung. In: spektrum.de. 3. September 2018, abgerufen am 13. Oktober 2023.
- ↑ Einstein's Quantum Riddle. PBS Nova, 9. Januar 2019, abgerufen am 21. Juli 2023 (englisch).
Literatur
- David I. Kaiser: Tackling Loopholes in Experimental Tests of Bell’s Inequality. In: Olival Freire (Hrsg.): The Oxford Handbook of the History of Quantum Interpretations. Oxford Academic, 2022, Kap. 13, S. 339–370, doi:10.1093/oxfordhb/9780198844495.013.0014, arxiv:2011.09296 (englisch).
- Wayne Myrvold, Marco Genovese, Abner Shimony: Bell’s Theorem. In: The Stanford Encyclopedia of Philosophy. Edward N. Zalta, September 2021 (englisch).
- Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, Stephanie Wehner: Bell nonlocality. In: Rev. Mod. Phys. Band 86, Nr. 2, 2014, S. 419–478, doi:10.1103/RevModPhys.86.419, arxiv:1303.2849 (englisch).
- Johannes Kofler: Endspiel für den lokalen Realismus. In: Physik in unserer Zeit. Band 46, Nr. 6, 2015, S. 288, doi:10.1002/piuz.201501412.
- R. Bertlmann, A. Zeilinger (Hrsg.): Quantum[Un]Speakables II. Springer, 2017, Teil VII, insbesondere Kapitel 26, 28 und 29, doi:10.1007/978-3-319-38987-5 (englisch).
- Jan-Åke Larsson: Loopholes in Bell Inequality Tests of Local Realism. In: J. Phys. A. Band 47, 2014, S. 424003, doi:10.1088/1751-8113/47/42/424003, arxiv:1407.0363 (englisch).
Auf dieser Seite verwendete Medien
Autor/Urheber: George Stamatiou based on png file of C.Thompson, Lizenz: CC BY-SA 3.0
Scheme of a "two-channel" Bell test
The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation can be set by the experimenter. Emerging signals from each channel are detected and coincidences counted by the coincidence monitor CM.
The svg file from George Stamatiou based on C.Thompson's work.Autor/Urheber: George Stamatiou inkscape svg based on C.Thompson's work (png), Lizenz: CC BY-SA 3.0
Setup for a "single-channel" Bell test The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a single channel (e.g. "pile of plates") polariser whose orientation can be set by the experimenter. Emerging signals are detected and coincidences counted by the coincidence monitor CM. George Stamatiou inkscape svg based on C.thompson's work (png)