Barnes-Hut-Algorithmus
Der Barnes-Hut-Algorithmus ist ein 1986 von Josh Barnes und Piet Hut veröffentlichtes Näherungsverfahren, das eine effektive Berechnung der Kräfte in einem N-Körper-Problem ermöglicht. Im Gegensatz zur direkten Aufsummierung der Kräfte, deren Rechenaufwand mit ansteigt, reduziert sich der Aufwand beim Barnes-Hut-Algorithmus auf .
Motivation
Die Simulation von N-Körper-Problemen ist eine Standardaufgabe der Astronomie. Bei einem solchen Problem bewegt sich eine Anzahl (N) von Körpern unter dem Einfluss einer Kraft, die wiederum von den Positionen aller andern Körper abhängt. Als Beispiel sei hier auf die Bewegung von Sternen im Gravitationsfeld einer Galaxie verwiesen. Die direkte Integration ist mit zunehmender Anzahl an Körpern sehr aufwendig, da die auf einen Körper wirkende Kraft die Summe aller Kräfte ist die von den anderen Körpern auf ihn wirken. Berechnungen auf Basis der direkten Kräftesummation werden daher mit steigender Körperanzahl (N > 10000) schnell uneffektiv, denn die Gesamtzahl der Kraftberechnungen ist:
Diesem Trend lässt sich zwar durch Verwendung hochparallelisierter Computerhardware (GPU) entgegenwirken, allerdings verschiebt sich das Problem damit lediglich zu größeren Teilchenanzahlen. Für effektive Simulationen mit mehreren Millionen oder gar Milliarden Partikeln sind Algorithmen notwendig, deren Berechnungsaufwand nicht quadratisch mit der Teilchenzahl ansteigt. Einer dieser Algorithmen ist der von Barnes und Hut.
Die Berechnungen für Wechselwirkende Galaxien ist ein typischer Anwendungsfall für Barnes-Hut-Simulationen.
Graphzeichnen
Die paarweise Berechnung von Kräften zwischen einer großen Anzahl von Objekten ist ebenfalls eine Problemstellung innerhalb des kräftebasierten Graphzeichnens als Teil der Informatik. Dabei werden die Kanten zwischen den Knoten eines Graphen als System von Federn interpretiert und der Graph soll so in die Ebene gezeichnet werden, dass die Federkräfte sich aufheben. Der Barnes-Hut-Algorithmus ermöglicht eine iterative Berechnung der Kräfte und Repositionierung der Knoten.[1]
Funktionsweise
Der Barnes-Hut-Algorithmus verringert die Anzahl zu berechnenden Kräfte durch geeignetes Zusammenfassen von Teilchengruppen zu Pseudoteilchen. Die Grundidee dabei ist, dass die von einer Partikelgruppe auf ein Einzelpartikel ausgeübte Kraft in sehr guter Näherung durch die Wirkung einer einzelnen Masse im Massenschwerpunkt der Partikelgruppe approximiert werden kann. So kann man beispielsweise die Kraft, die von der Andromeda-Galaxie auf die Sonne ausgeübt wird, sehr gut durch eine Punktmasse nähern, die sich im Zentrum der Andromeda-Galaxie befindet und die deren Masse hat. Diese Näherung ist allerdings nur zulässig, wenn der Abstand der Gruppe vom Einzelteilchen groß und der Gruppendurchmesser im Verhältnis zum Abstand klein ist. Das Verhältnis von Gruppendurchmesser zu Gruppenentfernung wird als Multipol-Akzeptanz-Kriterium (engl.: multipole acceptance criterion, MAC) bezeichnet:
Je kleiner , umso besser die Approximation. Überschreitet einen bestimmten Schwellwert, so sollte die Näherung nicht mehr angewendet werden, um größere Fehler zu vermeiden. Der Algorithmus setzt dieses Prinzip durch rekursives Unterteilen des Simulationsbereiches in Quadranten (2D) bzw. Oktanten (3D) um. Die Partikel werden in den Knoten der so entstandenen Baumstruktur gespeichert. Ist die Entfernung eines Knotens von einem Einzelteilchen groß genug, dann erfolgt die Kraftberechnung nicht mehr direkt zwischen den Teilchen, sondern zwischen dem Einzelteilchen und dem Massenschwerpunkt des Knotens.
Die gravitative Wirkung von Sternhaufen und Stern B auf Stern A kann infolge der großen Entfernung als Punktmasse approximiert werden. Doch auch innerhalb des Sternhaufens kann die Gravitationskraft des Sternhaufens auf Stern B durch eine Punktmasse angenähert werden, da Stern B weit genug vom Sternhaufen entfernt ist.
Siehe auch
Literatur
- Josh Barnes, Piet Hut: A hierarchical O(N log N) force-calculation algorithm. In: Nature. Band 324, Nr. 6096, Dezember 1986, S. 446–449, doi:10.1038/324446a0.
Weblinks
Deutsch
Englisch
- Video einer Partikelsimulation mit 8,7 Millionen Partikeln unter Verwendung des Barnes-Hut-Algorithmus gerechnet auf mehreren GPUs (youtube.com)
- PEPC – The Pretty Efficient Parallel Coulomb Solver, eine parallele open-source Implementation des Barnes-Hut-Algorithmus mit austauschbarem Wechselwirkungskern für vielseitige Anwendungen
- Fast Hierarchical Methods for the N-body Problem, Part 1, CS267, Lecture 24, 11. April 1996
Quellen
- ↑ Yifan Hu: Efficient, high-quality force-directed graph drawing. In: Mathematica Journal. Band 10, Nr. 1, 2006, S. 37–71 (mathematica-journal.com [PDF; abgerufen am 6. Dezember 2020]).
Auf dieser Seite verwendete Medien
Autor/Urheber: Ingo Berg, Lizenz: CC BY-SA 3.0
A: Die Kraft einer Partikelverteilung auf ein einzelnes Teilchen kann durch die Kraft eines Peseudoteilchens im Massenschwerpunkt der Gruppe angenähert werden, wenn der Abstand d nur groß genug ist.
Autor/Urheber: Ingo Berg, Lizenz: CC BY-SA 3.0
Simulation der interaktion zweier aneinander vorbeiziehender Galaxien. Die Simulation ähnelt der Whirlpool Galaxie basiert aber nicht auf exakten astronomischen Daten.
Autor/Urheber: Eclipse.sx, Lizenz: CC BY-SA 3.0
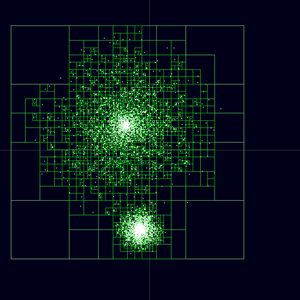
Vollständiger Barnes-Hut-Baum für eine aus 5000 Partikeln bestehende Verteilung, die zwei benachbarten Galaxien nachempfunden ist. Jeder Partikel befindet sich in einer eigenen Zelle.
Autor/Urheber: Eclipse.sx, Lizenz: CC BY-SA 3.0
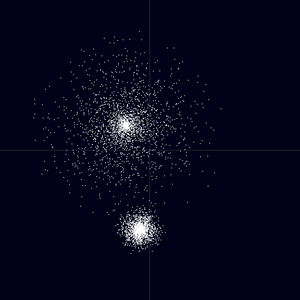
Partikelverteilung, die zwei benachbarten Galaxien nachempfunden ist.
Autor/Urheber: Eclipse.sx, Lizenz: CC BY-SA 3.0
Die Gravitative Wirkung von Sternhaufen und Stern B auf Stern A kann infolge der großen Entfernung als Punktmasse approximiert werden. Doch auch innerhalb des Sternhaufens kann die Gravitationskraft des Sternhaufens auf Stern B durch eine Punktmasse angenähert werden, da Stern B weit genug vom Sternhaufen entfernt ist.
Autor/Urheber: Eclipse.sx, Lizenz: CC BY-SA 3.0
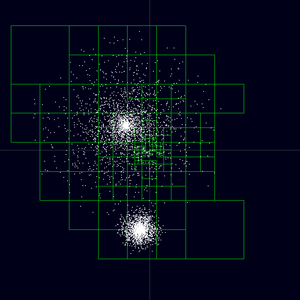
Barnes-Hut-Baum für eine Verteilung von 5000 Partikeln. Es werden nur die 146 knoten angezeigt werden, die zur Berechnung der Kraft auf ein Teilchen im Koordinatenursprung herangezogen werden.