Auxetisches Material

Auxetische Materialien (von altgriechisch αὐξητόςauxetos, deutsch ‚dehnbar‘) haben die ungewöhnliche Eigenschaft, sich bei einer Streckung quer zur Streckrichtung auszudehnen. Sie sind daher charakterisiert durch eine negative Poissonzahl (Querkontraktionszahl) ${\displaystyle \nu _{\mathrm {aux} }<0.}$, während die meisten üblichen Materialien wie Metalle, Polymere oder Beton eine positive Querkontraktionszahl im Bereich ${\displaystyle 0.<\nu <0.5}$ besitzen.

Beschreibung

(c) LZ6387 in der Wikipedia auf Deutsch, CC BY-SA 3.0

Auxetisches Netz im Kasten unten links: Eine vertikale Streckung hat eine horizontale Ausdehnung zur Folge (und umgekehrt). Hier ist nur das Prinzip dargestellt. Eigentlich sollte die gestreckte Quadratstruktur rechts mehr Fläche beanspruchen als die noch gefalteten Rauten links. Bei der Wabenstruktur oben ist es umgekehrt.

Zu den auxetischen Materialien gehören unter anderem hochverstrecktes Teflon und die Haut von Kuhzitzen^[1]. Schon im Jahre 1888 wurde von Woldemar Voigt (Physiker) eine negative Querkontraktionszahl von kristallinem Pyrit veröffentlicht^[2].

Eines der ersten künstlich hergestellten auxetischen Materialien, die RFS-Struktur (Rauten-Falt-Struktur)^[3], wurde 1978 von dem Berliner Forscher Karsten Pietsch erfunden. Er verwendete zwar nicht den Begriff Auxetik, beschreibt aber erstmals die zu Grunde liegende Hebelmechanik sowie deren nicht lineare mechanischen Reaktionen und gilt daher als Erfinder des in der Grafik oben dargestellten Auxetischen Netzes und der aus dem Satz des Pythagoras abgeleiteten Formel der auxetischen Querausdehnung:

Satz der auxetischen Querausdehnung:

${\displaystyle q={\sqrt {c^{2}-(c-z)^{2}}}}$

${\displaystyle q}$= Querausdehnung, ${\displaystyle c}$= Länge des Hebelarms, ${\displaystyle z}$= die Länge der einwirkenden Zugbewegung

Prinzip der auxetischen Hebelmechanik

Aus dem Satz der auxetischen Querausdehnung lässt sich unter der Berücksichtigung der Hebelgesetze (Kniehebel) die Dynamik und Kinematik der auxetischen Hebelmechanik von der geringsten bis zur größten Ausdehnung ableiten.

In späteren Veröffentlichungen relativiert er den Begriff Auxetik mit der Feststellung, dass es kein Vollmaterial aus einem Grundstoff mit einer negativen Poissonzahl geben kann, da ein auxetisches Material mindestens aus zwei unterschiedlichen Grundstoffen besteht und dessen auxetischer Effekt immer auf eine hebelmechanische Reaktion zurückzuführen ist. Darum kann auch die Berechnung der Querkontraktion nach Siméon Denis Poisson in der Festigkeitslehre nicht ohne Weiteres auf auxetische Materialien angewendet werden. Diese ist nur für Vollmaterialien definiert, die aus einem einzelnen Grundstoff bestehen.

Auxetischen Materialien bestehen in der Regel aus Grundstoffen, die selber eine neutrale oder positive Poissonzahl haben.

Die negative Poissonzahl hat nur begrenzte Anwendungsfälle, da sie in der Regel nur bei porösen oder Verbundmaterialien anzutreffen ist, die eine Volumenveränderung zulassen und deren hebelmechanische Reaktion eine Kraft/Weg-Umkehrung aufweist. Eine negative Poissonzahl lässt sich zwar berechnen, sie besitzt aber keine aussagekräftige Relevanz.^[4] Das Prinzip der auxetischen Materialien wurde erstmals 1987 im Wissenschaftsmagazin Science näher beschrieben.^[5]

Auxetisches Verhalten kann auf Molekül- oder Makroebene entstehen. Es ist bei verschiedenen Mineralschnitten zu beobachten. Dazu gehören Molybdän(IV)sulfid, Graphit, Labradorit und Augit. Ebenso kann man auxetisches Verhalten bei entsprechend geschnittenen Cristobalitdünnschliffen, Zink und Polypropylen zeigen.^[6]

Aufbau

Normale Materialien werden, wenn sie auseinandergezogen werden, in der Mitte dünner, da sie sich in Richtung des Zugs dehnen. Auxetische Materialien dagegen nehmen im Querschnitt zu, wenn an ihnen gezogen wird; sie weiten sich quer zur Zugrichtung.

Die Darstellung zeigt die beiden Querausdehnungseffekte der Rauten-Falt-Struktur(RFS)

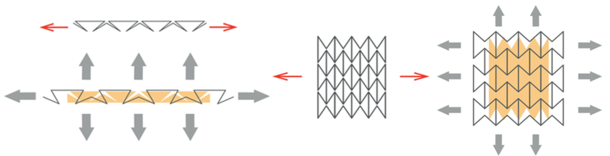
Dreidimensionale auxetische Materialien weiten sich in alle Richtungen quer zur Zugrichtung. Dabei handelt es sich meist um Makrostrukturen, die dem Material die auxetischen Eigenschaften verleihen, und nicht um eine Eigenschaft auf molekularer Ebene. Es gibt Materialien, die von Natur aus solche Strukturen aufweisen, und Materialien, die künstlich in eine auxetische Struktur gebracht werden, wie die Rautenfaltstruktur (RFS), die aus verschiedenen Grundstoffen hergestellt werden kann.

Anwendung

Auxetische Materialien besitzen sehr gute mechanische Eigenschaften wie hohe Werte für Schersteifigkeit, Eindringwiderstand, Bruchzähigkeit und Dissipation mechanischer Aufprallenergie^[7]. Deshalb sind auxetische Materialien beispielsweise für Leichtbauanwendungen geeignet.

Ausgehend von der auxetischen Mechanik, welche maßgeblich die mechanischen Strukturparameter wie z. B. Steifigkeit, thermisches und Schwingungsverhalten, Energieabsorptionsfähigkeit oder Zähigkeit prägt und überdurchschnittlich positiv beeinflusst, erreicht man bei gleichem oder leichterem Gewicht Leistungsniveaus, die mit üblichen Bauweisen nicht realisierbar sind.

Darüber hinaus ermöglicht die auxetische Mechanik völlig neuartige Funktionalitäten und Designlösungen für eine Vielzahl neuer Produkte mit gezielt einstellbaren Funktionseigenschaften. Deshalb sind auxetische Konstruktionsansätze sowohl aus wissenschaftlicher als auch wirtschaftlicher und gestalterischer Sicht von großer Bedeutung.

Künstliche Lungen, die aus auxetischen Materialien bestehen, können mehr Sauerstoff aufnehmen und Kohlenstoffdioxid abgeben. Auch in der Pharmazie sind Anwendungen denkbar: Wäre ein mit Medikamenten gefülltes Minidepot in ein Pflaster eingebaut, würde bei einer Schwellung der Wunde das Medikament freigesetzt, da der sich durch den Druck verringernde Querschnitt den enthaltenen Stoff herausdrücken würde.

Denkbar ist, Schutzausrüstungen für Sportler oder schusssichere Westen aus auxetischen Materialien herzustellen^[7]. Herkömmliche Sicherheitswesten bestehen aus Faserstoffen, die die Kraft des Projektils auf eine große Fläche verteilen und dadurch die Durchschlagskraft verringern. Beim Aufprall auf Westen aus auxetischen Materialien entsteht dagegen ein Bereich höherer Dichte und damit Eindringwiderstand. Dadurch werden Aufprallenergien wirksam dissipiert.

Weblinks

• Negative Poisson’s ratio materials (englisch)
• Auxetische Moleküle
• Bericht über Auxetik auf ORF.at
• Wunder-Stoff fasziniert mit bizarren Eigenschaften auf welt.de vom 27. November 2011
• Info über auxetische Materialien (englisch)
• Video eines auxetischen Schaums (abgerufen am 13. Februar 2022)

Einzelnachweise

1. ↑ Caroline Lees, Julian F.V. Vincent, J. Eric Hillerton: Poisson's ratio in skin. In: Bio-medical materials and engineering. Band 1, Nr. 1, 1991, S. 19–23, doi:10.3233/BME-1991-1104 (englisch). 
2. ↑ Woldemar Voigt: Bestimmung der Elasticitätsconstanten von Flussspath, Pyrit, Steinsalz, Sylvin. In: Annalen der Physik. Band 271, Nr. 12, 1888, S. 642–661, doi:10.1002/andp.18882711204. 
3. ↑ RFS-Struktur (Rauten-Falt-Struktur), In: Materialblog.de
4. ↑ Maria Burke: A stretch of the imagination. In: New Scientist. Band 154, Nr. 2085, 1997, S. 36–39 (englisch, newscientist.com [abgerufen am 13. November 2021]).  Auch: Volltext (Memento vom 26. August 2011 im Internet Archive).
5. ↑ Roderic Lakes: Foam Structures with a Negative Poisson’s Ratio. In: Science. Band 235, Nr. 4792, 1987, S. 1038–1040, doi:10.1126/science.235.4792.1038 (englisch). 
6. ↑ S. P. Tokmakova: Stereographic projections of Poisson’s ratio in auxetic crystals. In: physica status solidi (b). Band 242, Nr. 3, 2005, S. 721–729, doi:10.1002/pssb.200460389 (englisch). 
7. ↑ ^{a b} Andreas T. Wolf: Auxetische Materialien: Von einer wissenschaftlichen Kuriosität zu funktionalen Werkstoffen. In: Chemie in unserer Zeit. 2001, doi:10.1002/ciuz.202000067.