Abb. 1: Graph der Funktion arctan {\displaystyle \arctan } Abb. 2: Graph der Funktion arccot {\displaystyle \operatorname {arccot} } Arkustangens und Arkuskotangens sind zwei miteinander verwandte mathematische Arkusfunktionen . Sie sind die Umkehrfunktionen der geeignet eingeschränkten Tangens - und Kotangensfunktionen : Eine Einschränkung der ursprünglichen Definitionsbereiche ist nötig, weil Tangens und Kotangens periodische Funktionen sind. Man wählt beim Tangens das Intervall ] − π / 2 , π / 2 [ {\displaystyle ]-\pi /2,\pi /2[} ] 0 , π [ {\displaystyle ]0,\pi [} [ 1]
Zusammen mit Arkussinus und Arkuskosinus als Umkehrfunktionen des Sinus und Kosinus bildet der Arkustangens den Kern der Klasse der Arkusfunktionen . Zusammen mit den Areafunktionen sind sie in der komplexen Funktionentheorie Abwandlungen des komplexen Logarithmus , von dem sie auch die „Mehrdeutigkeit“ erben, die ihrerseits von der Periodizität der komplexen Exponentialfunktion herrührt.
Schreibweisen Mathematische Formeln verwenden für den Arkustangens als Formelzeichen arctan {\displaystyle \arctan } atan {\displaystyle \operatorname {atan} } tan ( − 1 ) {\displaystyle \tan ^{(-1)}} tan ⟨ − 1 ⟩ {\displaystyle \tan ^{\langle -1\rangle }} tan − 1 {\displaystyle \tan ^{-1}} [ 2] arccot , {\displaystyle \operatorname {arccot} ,} arcctg , {\displaystyle \operatorname {arcctg} ,} acot {\displaystyle \operatorname {acot} } cot − 1 {\displaystyle \cot ^{-1}} [ 3]
Aufgrund der heute für Umkehrfunktionen gebräuchlichen allgemeinen Schreibweise f − 1 {\displaystyle f^{-1}} tan − 1 {\displaystyle \tan ^{-1}} arctan {\displaystyle \arctan } Kehrwert des Tangens, dem Kotangens , führen kann (s. a. die Schreibweisen für die Iteration).
Eigenschaften Arkustangens Arkuskotangens Definitionsbereich x ∈ R {\displaystyle x\in \mathbb {R} } x ∈ R {\displaystyle x\in \mathbb {R} } Bildmenge − π 2 < f ( x ) < π 2 {\displaystyle -{\tfrac {\pi }{2}}<f(x)<{\tfrac {\pi }{2}}} 0 < f ( x ) < π {\displaystyle 0<f(x)<\pi } Monotonie streng monoton steigend streng monoton fallend Symmetrien Ungerade Funktion:arctan ( − x ) = − arctan x {\displaystyle \arctan(-x)=-\arctan x} Punktsymmetrie zu ( x = 0 , y = π 2 ) {\displaystyle \left(x=0,y={\tfrac {\pi }{2}}\right)} arccot x = π − arccot ( − x ) {\displaystyle \operatorname {arccot} x=\pi -\operatorname {arccot}(-x)} Asymptoten f ( x ) → ± π 2 {\displaystyle f(x)\to \pm {\tfrac {\pi }{2}}} x → ± ∞ {\displaystyle x\to \pm \infty } f ( x ) → π {\displaystyle f(x)\to \pi } x → − ∞ {\displaystyle x\to -\infty } f ( x ) → 0 {\displaystyle f(x)\to 0} x → + ∞ {\displaystyle x\to +\infty } Nullstellen x = 0 {\displaystyle x=0} keine Sprungstellen keine keine Polstellen keine keine Extrema keine keine Wendepunkte ( 0 , 0 ) {\displaystyle (0,0)} ( 0 , π 2 ) {\displaystyle \left(0,{\tfrac {\pi }{2}}\right)}
Wichtige Funktionswerte Die folgende Tabelle listet die wichtigen Funktionswerte der beiden Arkusfunktionen auf.[ 4]
x {\displaystyle x} arctan ( x ) {\displaystyle \arctan(x)} arccot ( x ) {\displaystyle \operatorname {arccot}(x)} 0 {\displaystyle 0} 0 ∘ {\displaystyle 0^{\circ }} 0 {\displaystyle 0} 90 ∘ {\displaystyle 90^{\circ }} π 2 {\displaystyle {\frac {\pi }{2}}} 1 3 3 {\displaystyle {\tfrac {1}{3}}{\sqrt {3}}} 30 ∘ {\displaystyle 30^{\circ }} π 6 {\displaystyle {\frac {\pi }{6}}} 60 ∘ {\displaystyle 60^{\circ }} π 3 {\displaystyle {\frac {\pi }{3}}} 1 {\displaystyle 1\,} 45 ∘ {\displaystyle 45^{\circ }} π 4 {\displaystyle {\frac {\pi }{4}}} 45 ∘ {\displaystyle 45^{\circ }} π 4 {\displaystyle {\frac {\pi }{4}}} 3 {\displaystyle {\sqrt {3}}} 60 ∘ {\displaystyle 60^{\circ }} π 3 {\displaystyle {\frac {\pi }{3}}} 30 ∘ {\displaystyle 30^{\circ }} π 6 {\displaystyle {\frac {\pi }{6}}}
Weitere wichtige Werte sind:
x {\displaystyle x} arctan ( x ) {\displaystyle \arctan(x)} arccot ( x ) {\displaystyle \operatorname {arccot}(x)} 2 − 3 {\displaystyle 2-{\sqrt {3}}} 15 ∘ {\displaystyle 15^{\circ }} π 12 {\displaystyle {\tfrac {\pi }{12}}} 75 ∘ {\displaystyle 75^{\circ }} 5 π 12 {\displaystyle {\tfrac {5\pi }{12}}} 1 5 25 − 10 5 {\displaystyle {\tfrac {1}{5}}{\sqrt {25-10{\sqrt {5}}}}} 18 ∘ {\displaystyle 18^{\circ }} π 10 {\displaystyle {\tfrac {\pi }{10}}} 72 ∘ {\displaystyle 72^{\circ }} 2 π 5 {\displaystyle {\tfrac {2\pi }{5}}} 5 − 2 5 {\displaystyle {\sqrt {5-2{\sqrt {5}}}}} 36 ∘ {\displaystyle 36^{\circ }} π 5 {\displaystyle {\tfrac {\pi }{5}}} 54 ∘ {\displaystyle 54^{\circ }} 3 π 10 {\displaystyle {\tfrac {3\pi }{10}}} 1 5 25 + 10 5 {\displaystyle {\tfrac {1}{5}}{\sqrt {25+10{\sqrt {5}}}}} 54 ∘ {\displaystyle 54^{\circ }} 3 π 10 {\displaystyle {\tfrac {3\pi }{10}}} 36 ∘ {\displaystyle 36^{\circ }} π 5 {\displaystyle {\tfrac {\pi }{5}}} 5 + 2 5 {\displaystyle {\sqrt {5+2{\sqrt {5}}}}} 72 ∘ {\displaystyle 72^{\circ }} 2 π 5 {\displaystyle {\tfrac {2\pi }{5}}} 18 ∘ {\displaystyle 18^{\circ }} π 10 {\displaystyle {\tfrac {\pi }{10}}} 2 + 3 {\displaystyle 2+{\sqrt {3}}} 75 ∘ {\displaystyle 75^{\circ }} 5 π 12 {\displaystyle {\tfrac {5\pi }{12}}} 15 ∘ {\displaystyle 15^{\circ }} π 12 {\displaystyle {\tfrac {\pi }{12}}}
Für Tangenswerte x > 1 {\displaystyle x>1} #Funktionalgleichungen .
Es gelten folgende Näherungen:
Arkustangens, maximale Abweichung unter 0,005 Radianten:[ 5]
arctan x ≈ { x 1 + 0 , 28 x 2 f u ¨ r | x | ≤ 1 π 2 − x x 2 + 0 , 28 f u ¨ r x > 1 − π 2 − x x 2 + 0 , 28 f u ¨ r x < − 1 {\displaystyle \arctan x\approx {\begin{cases}{\frac {x}{1+0{,}28x^{2}}}&\;\mathrm {f{\ddot {u}}r} \;|x|\leq 1\\{\frac {\pi }{2}}-{\frac {x}{x^{2}+0{,}28}}&\;\mathrm {f{\ddot {u}}r} \;x>1\\-{\frac {\pi }{2}}-{\frac {x}{x^{2}+0{,}28}}&\;\mathrm {f{\ddot {u}}r} \;x<-1\end{cases}}} Eine weitere Berechnungsmöglichkeit bietet CORDIC .
Arkuskotangens:
arccot x ≈ 3 x 3 x 2 − 1 f u ¨ r x ≫ 1 {\displaystyle \operatorname {arccot} x\approx {\frac {3x}{3x^{2}-1}}\quad \;\mathrm {f{\ddot {u}}r} \;x\gg 1}
Reihenentwicklungen
MacLaurinsche Reihen Die Taylorreihe des Arkustangens mit dem Entwicklungspunkt x = 0 {\displaystyle x=0}
arctan x = ∑ k = 0 ∞ ( − 1 ) k x 2 k + 1 2 k + 1 = x − 1 3 x 3 + 1 5 x 5 − 1 7 x 7 + ⋯ {\displaystyle \arctan x=\sum _{k=0}^{\infty }(-1)^{k}{\frac {x^{2k+1}}{2k+1}}=x-{\frac {1}{3}}x^{3}+{\frac {1}{5}}x^{5}-{\frac {1}{7}}x^{7}+\dotsb } Die Taylorreihe des Arkuskotangens mit dem Entwicklungspunkt x = 0 {\displaystyle x=0}
arccot x = π 2 − ∑ k = 0 ∞ ( − 1 ) k x 2 k + 1 2 k + 1 = π 2 − x + 1 3 x 3 − 1 5 x 5 + 1 7 x 7 − ⋯ {\displaystyle \operatorname {arccot} x={\frac {\pi }{2}}-\sum _{k=0}^{\infty }(-1)^{k}{\frac {x^{2k+1}}{2k+1}}={\frac {\pi }{2}}-x+{\frac {1}{3}}x^{3}-{\frac {1}{5}}x^{5}+{\frac {1}{7}}x^{7}-\dotsb } Diese Reihen konvergieren genau dann, wenn | x | ≤ 1 {\displaystyle |x|\leq 1} x ≠ ± i {\displaystyle x\neq \pm \mathrm {i} } | x | > 1 {\displaystyle |x|>1} | x | < 1 {\displaystyle |x|<1} Funktionalgleichung benutzen oder (um ohne π {\displaystyle \pi }
arctan x = 2 arctan x 1 + 1 + x 2 . {\displaystyle \arctan x=2\,\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}.} Durch mehrfache Anwendung dieser Formel lässt sich der Betrag des Arguments beliebig verkleinern, was eine sehr effiziente Berechnung durch die Reihe ermöglicht. Schon nach einmaliger Anwendung obiger Formel hat man ein Argument mit | x | < 1 , {\displaystyle |x|<1,} | x | {\displaystyle |x|}
Wegen cot α = 1 tan α {\displaystyle \textstyle \cot \alpha ={\frac {1}{\tan \alpha }}} x = ∞ {\displaystyle x=\infty }
arccot x = ∑ k = 0 ∞ ( − 1 ) k ⋅ x − 2 k − 1 2 k + 1 = 1 x − 1 3 x 3 + 1 5 x 5 − 1 7 x 7 + ⋯ {\displaystyle \operatorname {arccot} x=\sum _{k=0}^{\infty }(-1)^{k}\cdot {\frac {x^{-2k-1}}{2k+1}}={\frac {1}{x}}-{\frac {1}{3x^{3}}}+{\frac {1}{5x^{5}}}-{\frac {1}{7x^{7}}}+\dotsb } Sie konvergiert für x ≥ 1 {\displaystyle x\geq 1} x ≤ − 1 , {\displaystyle x\leq -1,} arccot x − π . {\displaystyle \operatorname {arccot} x-\pi .} x < 0 {\displaystyle x<0} unstetigen , aber punktsymmetrischen und am unendlich fernen Punkt stetigen Wert arccot x − π {\displaystyle \operatorname {arccot} x-\pi }
Reihen mit den Zentralbinomialkoeffizienten Die folgenden Reihen mit den Zentralbinomialkoeffizienten konvergieren für alle Zahlen x ∈ R {\displaystyle x\in \mathbb {R} } [ 6]
arctan ( x ) = ∑ n = 1 ∞ ( 2 x ) 2 n − 1 n CBC ( n ) ( x 2 + 1 ) n {\displaystyle \arctan(x)=\sum _{n=1}^{\infty }{\frac {(2\,x)^{2n-1}}{n\operatorname {CBC} (n)(x^{2}+1)^{n}}}} arctan ( x ) 2 = ∑ n = 1 ∞ ( 2 x ) 2 n 2 n 2 CBC ( n ) ( x 2 + 1 ) n {\displaystyle \arctan(x)^{2}=\sum _{n=1}^{\infty }{\frac {(2\,x)^{2n}}{2\,n^{2}\operatorname {CBC} (n)(x^{2}+1)^{n}}}} Der n {\displaystyle n} Zentralbinomialkoeffizient für eine natürliche Zahl n {\displaystyle n}
CBC ( n ) = ( 2 n n ) = ( 2 n ) ! ( n ! ) 2 = Π ( 2 n ) Π ( n ) 2 {\displaystyle \operatorname {CBC} (n)={2n \choose n}={\frac {(2n)!}{(n!)^{2}}}={\frac {\Pi (2n)}{\Pi (n)^{2}}}} dabei ist Π ( x ) = x ! = Γ ( x + 1 ) {\displaystyle \Pi (x)=x!=\Gamma (x+1)} Gaußsche Pifunktion .
Funktionalgleichungen Statt aus Argumenten x {\displaystyle x} y = 1 x {\displaystyle y={\frac {1}{x}}}
arctan x = sgn ( x ) ⋅ π 2 − arctan 1 x {\displaystyle \arctan x=\operatorname {sgn}(x)\cdot {\frac {\pi }{2}}-\arctan {\frac {1}{x}}} Gleiches gilt für den Arkuskotangens:
arccot x = ( 2 − sgn ( x ) ) ⋅ π 2 − arccot 1 x {\displaystyle \operatorname {arccot} x=\left(2-\operatorname {sgn}(x)\right)\cdot {\frac {\pi }{2}}-\operatorname {arccot} {\frac {1}{x}}} Wenn man (bspw. durch die erste Ersetzung) bei einem Argument (einem Tangenswert) y ∈ [ 0 , 1 ] {\displaystyle y\in [0,1]} y ∈ [ 3 3 , 1 ] {\displaystyle \textstyle y\in \left[{\frac {\sqrt {3}}{3}},1\right]}
arctan y = π 4 − 1 2 ⋅ arctan ( 1 − y 2 2 y ) , {\displaystyle \arctan y={\frac {\pi }{4}}-{\frac {1}{2}}\cdot \arctan \left({\frac {1-y^{2}}{2y}}\right),} anwenden, sodass mit z = 1 − y 2 2 y {\displaystyle \textstyle z={\frac {1-y^{2}}{2y}}} jedem Fall (jetzt z {\displaystyle z} y {\displaystyle y} [ 0 , 3 3 ] {\displaystyle \textstyle \left[0,{\frac {\sqrt {3}}{3}}\right]} 3 3 ≈ 0,577 350 … {\displaystyle {\tfrac {\sqrt {3}}{3}}\approx 0{,}577350\dotso }
Weitere Beziehungen arccot x = { arctan 1 x f u ¨ r x > 0 arctan ( 1 x ) + π f u ¨ r x < 0 {\displaystyle \operatorname {arccot} {x}={\begin{cases}\arctan \displaystyle {\frac {1}{x}}&\;\mathrm {f{\ddot {u}}r} \;x>0\\\arctan \displaystyle \left({\frac {1}{x}}\right)+\pi &\;\mathrm {f{\ddot {u}}r} \;x<0\\\end{cases}}} arctan x = { arccot 1 x f u ¨ r x > 0 arccot ( 1 x ) − π f u ¨ r x < 0 {\displaystyle \arctan {x}={\begin{cases}\operatorname {arccot} \displaystyle {\frac {1}{x}}&\;\mathrm {f{\ddot {u}}r} \;x>0\\\operatorname {arccot} \displaystyle \left({\frac {1}{x}}\right)-\pi &\;\mathrm {f{\ddot {u}}r} \;x<0\\\end{cases}}} arccot 1 x − arctan x = arccot x − arctan 1 x = { 0 f u ¨ r x > 0 π f u ¨ r x < 0 {\displaystyle \operatorname {arccot} {\frac {1}{x}}-\arctan {x}=\operatorname {arccot} {x}-\arctan {\frac {1}{x}}={\begin{cases}0&\;\mathrm {f{\ddot {u}}r} \;x>0\\\pi &\;\mathrm {f{\ddot {u}}r} \;x<0\\\end{cases}}} arctan x + arccot x = π 2 {\displaystyle \arctan {x}+\operatorname {arccot} {x}={\frac {\pi }{2}}} Wegen der Punktsymmetrie arctan ( − x ) = − arctan ( x ) {\displaystyle \arctan(-x)=-\arctan(x)} ( x , y ) {\displaystyle (x,y)} ( − x , − y ) {\displaystyle (-x,-y)}
Additionstheoreme Die Additionstheoreme für Arkustangens und Arkuskotangens erhält man mit Hilfe der Additionstheoreme für Tangens und Kotangens :
arctan x + arctan y = { arctan ( tan ( arctan x + arctan y ) ) = arctan ( x + y 1 − x y ) wenn x y < 1 π + arctan ( tan ( arctan x + arctan y ) ) = π + arctan ( x + y 1 − x y ) wenn x + y ≥ 0 und x y > 1 − π + arctan ( tan ( arctan x + arctan y ) ) = − π + arctan ( x + y 1 − x y ) wenn x + y < 0 und x y > 1 {\displaystyle \arctan x+\arctan y=\left\{{\begin{matrix}\arctan(\tan(\arctan x+\arctan y))=\arctan \left({\frac {x+y}{1-xy}}\right)&{\text{wenn }}xy<1\\\pi +\arctan(\tan(\arctan x+\arctan y))=\pi +\arctan \left({\frac {x+y}{1-xy}}\right)&{\text{wenn }}x+y\geq 0{\text{ und }}xy>1\\-\pi +\arctan(\tan(\arctan x+\arctan y))=-\pi +\arctan \left({\frac {x+y}{1-xy}}\right)&{\text{wenn }}x+y<0{\text{ und }}xy>1\\\end{matrix}}\right.} arccot x + arccot y = { arccot ( cot ( arccot x + arccot y ) ) = arccot ( x y − 1 x + y ) wenn x + y > 0 π + arccot ( cot ( arccot x + arccot y ) ) = π + arccot ( x y − 1 x + y ) wenn x + y < 0 {\displaystyle \operatorname {arccot} x+\operatorname {arccot} y=\left\{{\begin{matrix}\operatorname {arccot}(\cot(\operatorname {arccot} x+\operatorname {arccot} y))=\operatorname {arccot} \left({\frac {xy-1}{x+y}}\right)&{\text{wenn }}x+y>0\\\pi +\operatorname {arccot}(\cot(\operatorname {arccot} x+\operatorname {arccot} y))=\pi +\operatorname {arccot} \left({\frac {xy-1}{x+y}}\right)&{\text{wenn }}x+y<0\\\end{matrix}}\right.} Daraus folgt insbesondere für doppelte Funktionswerte
2 arctan x = { arctan ( 2 x 1 − x 2 ) wenn x 2 < 1 π + arctan ( 2 x 1 − x 2 ) wenn x ≥ 0 und x 2 > 1 − π + arctan ( 2 x 1 − x 2 ) wenn x < 0 und x 2 > 1 {\displaystyle 2\arctan x=\left\{{\begin{matrix}\arctan \left({\frac {2x}{1-x^{2}}}\right)&{\text{wenn }}x^{2}<1\\\pi +\arctan \left({\frac {2x}{1-x^{2}}}\right)&{\text{wenn }}x\geq 0{\text{ und }}x^{2}>1\\-\pi +\arctan \left({\frac {2x}{1-x^{2}}}\right)&{\text{wenn }}x<0{\text{ und }}x^{2}>1\\\end{matrix}}\right.} 2 arccot x = { arccot ( x 2 − 1 2 x ) wenn x > 0 π + arccot ( x 2 − 1 2 x ) wenn x < 0 {\displaystyle 2\operatorname {arccot} x=\left\{{\begin{matrix}\operatorname {arccot} \left({\frac {x^{2}-1}{2x}}\right)&{\text{wenn }}x>0\\\pi +\operatorname {arccot} \left({\frac {x^{2}-1}{2x}}\right)&{\text{wenn }}x<0\\\end{matrix}}\right.} Aus dem ersten Gesetz lässt sich für hinreichend kleine x , y {\displaystyle x,y}
x ⊕ y := tan ( arctan x + arctan y ) = x + y 1 − x y {\displaystyle x\oplus y:=\tan(\arctan x+\arctan y)={\frac {x+y}{1-xy}}} das Gruppengesetz ⊕ {\displaystyle \oplus }
1 2 ⊕ 1 3 = 1 2 + 1 3 1 − 1 6 = 1 , {\displaystyle {\frac {1}{2}}\oplus {\frac {1}{3}}={\frac {{\frac {1}{2}}+{\frac {1}{3}}}{1-{\frac {1}{6}}}}=1,} woraus sich
arctan 1 2 + arctan 1 3 = arctan 1 2 + 1 3 1 − 1 6 = arctan 1 = π 4 {\displaystyle \arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}=\arctan {\frac {{\frac {1}{2}}+{\frac {1}{3}}}{1-{\frac {1}{6}}}}=\arctan {1}={\frac {\pi }{4}}} errechnet. Ferner gilt
1 n ⊕ 1 4 n 3 + 3 n = 4 n 3 + 4 n 4 n 4 + 3 n 2 − 1 = 4 n ( n 2 + 1 ) ( 4 n 2 − 1 ) ( n 2 + 1 ) = 4 n 4 n 2 − 1 = 2 ⊙ 1 2 n {\displaystyle {\frac {1}{n}}\oplus {\frac {1}{4n^{3}+3n}}={\frac {4n^{3}+4n}{4n^{4}+3n^{2}-1}}={\frac {4n(n^{2}+1)}{(4n^{2}-1)(n^{2}+1)}}={\frac {4n}{4n^{2}-1}}=2\odot {\frac {1}{2n}}} und dementsprechend
arctan 1 n = 2 arctan 1 2 n − arctan 1 4 n 3 + 3 n . {\displaystyle \arctan {\frac {1}{n}}=2\,\arctan {\frac {1}{2n}}-\arctan {\frac {1}{4n^{3}+3n}}.} Die zwei Gleichungen als Arkuskotangens geschrieben:
arccot 2 + arccot 3 = arccot 6 − 1 2 + 3 = arccot 1 = π 4 {\displaystyle \operatorname {arccot} {2}+\operatorname {arccot} {3}=\operatorname {arccot} {\frac {6-1}{2+3}}=\operatorname {arccot} {1}={\frac {\pi }{4}}} und
arccot n = 2 arccot ( 2 n ) − arccot ( 4 n 3 + 3 n ) . {\displaystyle \operatorname {arccot} {n}=2\,\operatorname {arccot}(2n)-\operatorname {arccot}(4n^{3}+3n).}
Die Reihenentwicklung kann dazu verwendet werden, die Zahl π mit beliebiger Genauigkeit zu berechnen: Die einfachste Formel ist der Spezialfall x = 1 , {\displaystyle x=1,} Leibniz-Formel
π 4 = 1 − 1 3 + 1 5 − 1 7 + ⋯ {\displaystyle {\frac {\pi }{4}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\dotsb } Da sie nur extrem langsam (logarithmisch) konvergiert, verwendete John Machin 1706 die Formel
π 4 = 4 arccot 5 − arccot 239 , {\displaystyle {\frac {\pi }{4}}=4\,\operatorname {arccot} {5}-\operatorname {arccot} {239},} um die ersten 100 Nachkommastellen von π {\displaystyle \pi } (linear) und wird auch heute noch für die Berechnung von π {\displaystyle \pi }
Im Laufe der Zeit wurden noch mehr Formeln dieser Art gefunden. Ein Beispiel stammt von Carl Størmer (1896):
π 4 = 44 arccot 57 + 7 arccot 239 − 12 arccot 682 + 24 arccot 12943 , {\displaystyle {\frac {\pi }{4}}=44\,\operatorname {arccot} {57}+7\,\operatorname {arccot} {239}-12\,\operatorname {arccot} {682}+24\,\operatorname {arccot} {12943},} [ 7] was gleichbedeutend damit ist, dass der Realteil und der Imaginärteil der Gaußschen Zahl
( 57 + i ) 44 ( 239 + i ) 7 ( 682 − i ) 12 ( 12943 + i ) 24 = ( 1 + i ) ⋅ n {\displaystyle (57+\mathrm {i} )^{44}\,(239+\mathrm {i} )^{7}\,(682-\mathrm {i} )^{12}\,(12943+\mathrm {i} )^{24}=(1+\mathrm {i} )\cdot n} n ∈ Z {\displaystyle n\in \mathbb {Z} } gleich sind.[ 8]
Gleiches gilt für die Formel von John Machin, wobei es hier um die Gaußsche Zahl
( 5 + i ) 4 ( 239 − i ) = ( 1 + i ) ⋅ 114244 {\displaystyle (5+\mathrm {i} )^{4}\,(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 114244} geht, die mit einem Taschenrechner berechnet werden kann.
Komplexer Arkustangens und Arkuskotangens Lässt man komplexe Argumente und Werte zu, so hat man
arctan ( a + b i ) = { 1 2 ( arctan a 2 + b 2 − 1 2 a + π 2 sgn ( a ) ) a ≠ 0 0 a = 0 , | b | ≤ 1 π 2 sgn ( b ) a = 0 , | b | > 1 } {\displaystyle \arctan(a+b\,\mathrm {i} )=\left\{{\begin{array}{ll}\displaystyle {\frac {1}{2}}\,\left(\arctan {\frac {a^{2}+b^{2}-1}{2a}}+{\frac {\pi }{2}}\,\operatorname {sgn}(a)\right)&\;a\neq 0\\0&\;a=0,\,|b|\leq 1\\\displaystyle {\frac {\pi }{2}}\,\operatorname {sgn}(b)&\;a=0,\,|b|>1\\\end{array}}\right\}}
+ i ⋅ 1 2 artanh 2 b a 2 + b 2 + 1 {\displaystyle {}+\mathrm {i} \cdot {\frac {1}{2}}\,\operatorname {artanh} {\frac {2b}{a^{2}+b^{2}+1}}} a , b ∈ R , {\displaystyle a,b\in \mathbb {R} ,} eine Darstellung, die quasi schon in Real- und Imaginärteil aufgespalten ist. Wie im Reellen gilt
arccot ( z ) = π 2 − arctan ( z ) {\displaystyle \operatorname {arccot}(z)={\frac {\pi }{2}}-\arctan(z)} mit z = a + b i . {\displaystyle z=a+b\,\mathrm {i} .}
Man kann im Komplexen den Arkustangens (wie auch den Arkuskotangens) durch ein Integral und durch den komplexen Logarithmus ausdrücken:
arctan z = ∫ 0 z d t 1 + t 2 = 1 2 ∫ 0 z ( d t 1 + i t + d t 1 − i t ) = ln ( 1 + i z ) − ln ( 1 − i z ) 2 i = 1 2 i ln 1 + i z 1 − i z {\displaystyle {\begin{array}{ll}\displaystyle \arctan z=\int _{0}^{z}{\frac {\mathrm {d} t}{1+t^{2}}}&\displaystyle ={\frac {1}{2}}\,\int _{0}^{z}\left({\frac {\mathrm {d} t}{1+\mathrm {i} t}}+{\frac {\mathrm {d} t}{1-\mathrm {i} t}}\right)\\\displaystyle ={\frac {\ln(1+\mathrm {i} z)-\ln(1-\mathrm {i} z)}{2\mathrm {i} }}&\displaystyle ={\frac {1}{2\mathrm {i} }}\,\ln {\frac {1+\mathrm {i} z}{1-\mathrm {i} z}}\end{array}}} für z {\displaystyle z}
| C | := C ∖ { i y | y ∈ R , | y | ≥ 1 } . {\displaystyle {}^{|}\mathbb {C} _{|}:=\mathbb {C} \setminus \{\mathrm {i} y\,|\,y\in \mathbb {R} ,|y|\geq 1\}.} Integrationsweg , der die imaginäre Achse nicht kreuzt außer evtl. im Einheitskreis . Es ist in diesem Gebiet
| C | {\displaystyle {}^{|}\mathbb {C} _{|}} [ 9]
Der Arkustangens spielt eine wesentliche Rolle bei der symbolischen Integration von Ausdrücken der Form
1 a x 2 + b x + c . {\displaystyle {\frac {1}{ax^{2}+bx+c}}.} Ist die Diskriminante D = b 2 − 4 a c {\displaystyle D=b^{2}-4ac} Partialbruchzerlegung bestimmen. Ist die Diskriminante negativ, so kann man den Ausdruck durch die Substitution
t = 2 a x + b − D {\displaystyle t={\frac {2ax+b}{\sqrt {-D}}}} in die Form
4 a − D 1 1 + t 2 {\displaystyle {\frac {4a}{-D}}\,{\frac {1}{1+t^{2}}}} bringen; eine Stammfunktion ist also
2 − D arctan 2 a x + b − D . {\displaystyle {\frac {2}{\sqrt {-D}}}\,\arctan {\frac {2ax+b}{\sqrt {-D}}}.} Und so entsteht das Endresultat:
1 a x 2 + b x + c = d d x [ 2 4 a c − b 2 arctan ( 2 a x + b 4 a c − b 2 ) ] {\displaystyle {\frac {1}{ax^{2}+bx+c}}={\frac {\mathrm {d} }{\mathrm {d} x}}{\biggl [}{\frac {2}{\sqrt {4ac-b^{2}}}}\arctan {\biggl (}{\frac {2ax+b}{\sqrt {4ac-b^{2}}}}{\biggr )}{\biggr ]}}
Umrechnung ebener kartesischer Koordinaten in polare Ist ein Punkt P {\displaystyle {\mathsf {P}}} Polarkoordinaten ( r , φ ) {\displaystyle (r,\varphi )} kartesischen Koordinaten ( x , y ) {\displaystyle (x,y)}
x = r ⋅ cos ( φ ) y = r ⋅ sin ( φ ) {\displaystyle {\begin{array}{ll}x=r\cdot \cos(\varphi )\\y=r\cdot \sin(\varphi )\\\end{array}}} } ( P → K ) {\displaystyle {\biggr \}}\;({\text{P}}\to {\text{K}})}
bestimmt.
Die Umrechnung in der Gegenrichtung ist etwas komplizierter. Auf jeden Fall gehört der Abstand
r = x 2 + y 2 {\displaystyle r={\sqrt {x^{2}+y^{2}}}} ( K → P r ) {\displaystyle ({\text{K}}\to {\text{P}}_{r})}
des Punktes P {\displaystyle {\mathsf {P}}} O ( 0 , 0 ) {\displaystyle {\mathsf {O}}(0,0)} r = 0 , {\displaystyle r=0,} x = y = 0 , {\displaystyle x=y=0,} φ ∈ R {\displaystyle \varphi \in \mathbb {R} }
Ist aber r ≠ 0 , {\displaystyle r\neq 0,} φ , {\displaystyle \varphi ,} sin {\displaystyle \sin } cos {\displaystyle \cos } Periode 2 π {\displaystyle 2\pi } ( P → K ) {\displaystyle ({\text{P}}\to {\text{K}})} modulo 2 π Z {\displaystyle 2\pi \mathbb {Z} } φ {\displaystyle \varphi } φ + 2 π n {\displaystyle \varphi +2\pi n} n ∈ Z {\displaystyle n\in \mathbb {Z} }
Trigonometrische Umkehrfunktionen sind erforderlich, um von Längen zu Winkeln zu kommen. Hier zwei Beispiele, bei denen der Arkustangens zum Einsatz kommt.
Der simple Arkustangens φ = arctan ( y x ) {\displaystyle \varphi =\arctan \left({\frac {y}{x}}\right)} π {\displaystyle \pi } π {\displaystyle \pi }
Abb. 3: φ als Außenwinkel eines gleichschenkligen Dreiecks
Halber Winkel In der nebenstehenden Abb. 3[ 10] Polarachse (die mit der + x {\displaystyle +x} r {\displaystyle r} − x {\displaystyle -x} O {\displaystyle {\mathsf {O}}} N . {\displaystyle {\mathsf {N}}.} N O P {\displaystyle {\mathsf {NOP}}} gleichschenkliges , sodass die Winkel ∢ P N O {\displaystyle \sphericalangle {\mathsf {PNO}}} ∢ O P N {\displaystyle \sphericalangle {\mathsf {OPN}}} Außenwinkel φ {\displaystyle \varphi } N O P . {\displaystyle {\mathsf {NOP}}.} Polarwinkel ∢ X O P . {\displaystyle \sphericalangle {\mathsf {XOP}}.} Abszissenpunkt A {\displaystyle {\mathsf {A}}} N A P {\displaystyle {\mathsf {NAP}}}
tan ( φ 2 ) = | Gegenkathete P A | | Ankathete A N | = y r + x , {\displaystyle \tan \left({\frac {\varphi }{2}}\right)={\frac {|{\text{Gegenkathete }}{\mathsf {PA}}|}{|{\text{Ankathete }}{\mathsf {AN}}|}}={\frac {y}{r+x}},} was nach φ {\displaystyle \varphi }
φ = 2 ⋅ arctan ( y r + x ) {\displaystyle \varphi =2\cdot \arctan \left({\frac {y}{r+x}}\right)} ( K → P φ ( A ) ) {\displaystyle ({\text{K}}\to {\text{P}}_{\varphi }(A))}
ergibt. Die Gleichung versagt, wenn r + x = 0 {\displaystyle r+x=0} | x | ≤ | r | ⇒ x = − | r | {\displaystyle |x|\leq |r|\Rightarrow x=-|r|} y = 0 {\displaystyle y=0} x = 0 {\displaystyle x=0} x < 0 , {\displaystyle x<0,} ( P → K ) {\displaystyle ({\text{P}}\to {\text{K}})} φ = + π {\displaystyle \varphi =+\pi } φ = − π {\displaystyle \varphi =-\pi } erfüllt.[ 11] Das ist in Einklang mit den Bildmengen ] − π , + π ] {\displaystyle ]-\pi ,+\pi ]} [ − π , + π [ {\displaystyle [-\pi ,+\pi [}
Ein anderer Weg, um zu einem vollwertigen Polarwinkel zu kommen, ist in vielen Programmiersprachen und Tabellenkalkulationen gewählt worden, und zwar eine erweiterte Funktion, die mit den beiden kartesischen Koordinaten beschickt wird und die damit genügend Information hat, um den Polarwinkel modulo 2 π Z , {\displaystyle 2\pi \mathbb {Z} ,} ] − π , π ] , {\displaystyle ]-\pi ,\pi ],}
φ = arctan2 ( x , y ) {\displaystyle \varphi =\operatorname {arctan2} (x,y)} ( K → P φ ( B ) ) {\displaystyle ({\text{K}}\to {\text{P}}_{\varphi }(B))}
Zusammen mit der Gleichung ( K → P r ) {\displaystyle {\color {Blue}({\text{K}}\to {\text{P}}_{r})}} ( K → P φ ( A ) ) {\displaystyle {\color {Blue}({\text{K}}\to {\text{P}}_{\varphi }(A))}} ( K → P φ ( B ) ) {\displaystyle {\color {Blue}({\text{K}}\to {\text{P}}_{\varphi }(B))}} ( P → K ) {\displaystyle {\color {Blue}({\text{P}}\to {\text{K}})}}
x = r cos φ {\displaystyle x=r\cos \varphi } y = r sin φ {\displaystyle y=r\sin \varphi } und zwar für ( x , y ) = ( 0 , 0 ) {\displaystyle (x,y)=(0,0)} φ ∈ R . {\displaystyle \varphi \in \mathbb {R} .}
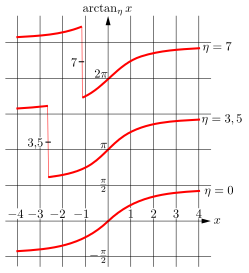
Arkustangens mit Lageparameter Abb. 4: Arkustangens mit Lageparameter In vielen Anwendungsfällen soll die Lösung y {\displaystyle y} x = tan y {\displaystyle x=\tan y} η {\displaystyle \eta } η {\displaystyle \eta }
y = arctan η x := arctan x + π ⋅ rni η − arctan x π . {\displaystyle y=\arctan _{\eta }x:=\arctan x+\pi \cdot \operatorname {rni} {\frac {\eta -\arctan x}{\pi }}.} Die Funktion rni {\displaystyle \operatorname {rni} }
Ableitungen Arkustangens:
d d x arctan ( x ) = 1 1 + x 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\arctan(x)={\frac {1}{1+x^{2}}}} Arkuskotangens:
d d x arccot ( x ) = − 1 1 + x 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arccot}(x)=-{\frac {1}{1+x^{2}}}}
Integrale
Standardisierte Integraldarstellungen Arkustangens und Arkuskotangens haben folgende standardisierte Integraldarstellungen:
arctan ( x ) = ∫ 0 x 1 t 2 + 1 d t = ∫ 0 1 x x 2 y 2 + 1 d y {\displaystyle \arctan(x)=\int _{0}^{x}{\frac {1}{t^{2}+1}}\,\mathrm {d} t=\int _{0}^{1}{\frac {x}{x^{2}y^{2}+1}}\,\mathrm {d} y} arccot ( x ) = ∫ x ∞ 1 t 2 + 1 d t = π 2 − ∫ 0 1 x x 2 y 2 + 1 d y {\displaystyle \operatorname {arccot}(x)=\int _{x}^{\infty }{\frac {1}{t^{2}+1}}\,\mathrm {d} t={\frac {\pi }{2}}-\int _{0}^{1}{\frac {x}{x^{2}y^{2}+1}}\,\mathrm {d} y}
Die Arkustangensfunktion hat folgende Integralidentität mit der Gaussschen Fehlerfunktion erf(x):
arctan ( x ) = ∫ 0 ∞ π exp ( − y 2 ) e r f ( x y ) d y {\displaystyle \arctan(x)=\int _{0}^{\infty }{\sqrt {\pi }}\,\exp(-y^{2})\,\mathrm {erf} (xy)\,\mathrm {d} y}
Mit der nicht normierten Fehlerfunktion kann diese Identität auch so geschrieben werden:
arctan ( x ) = ∫ 0 ∞ 2 exp ( − y 2 ) e r f ∗ ( x y ) d y {\displaystyle \arctan(x)=\int _{0}^{\infty }2\exp(-y^{2})\,\mathrm {erf} ^{*}(xy)\,\mathrm {d} y} e r f ∗ ( v ) = ∫ 0 v exp ( − w 2 ) d w {\displaystyle \mathrm {erf} ^{*}(v)=\int _{0}^{v}\exp(-w^{2})\,\mathrm {d} w} Durch Ableiten dieser Integralidentität entsteht die Ableitung des Arkustangens:
d d x ∫ 0 ∞ 2 exp ( − y 2 ) e r f ∗ ( x y ) d y = ∫ 0 ∞ 2 y exp ( − y 2 ) exp ( − x 2 y 2 ) d y = {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\int _{0}^{\infty }2\exp(-y^{2})\,\mathrm {erf} ^{*}(xy)\,\mathrm {d} y=\int _{0}^{\infty }2y\exp(-y^{2})\exp(-x^{2}y^{2})\,\mathrm {d} y=} = ∫ 0 ∞ 2 y exp [ − ( x 2 + 1 ) y 2 ] d y = 1 x 2 + 1 {\displaystyle =\int _{0}^{\infty }2y\exp {\bigl [}-(x^{2}+1)\,y^{2}{\bigr ]}\,\mathrm {d} y={\frac {1}{x^{2}+1}}} Die genannte Integralidentität ist bezüglich x eine Ursprungsfunktion.
Wenn der Wert x = 1 {\displaystyle x=1}
π 4 = arctan ( 1 ) = ∫ 0 ∞ 2 exp ( − y 2 ) e r f ∗ ( y ) d y = [ e r f ∗ ( y ) 2 ] y = 0 y = ∞ = lim y → ∞ e r f ∗ ( y ) 2 {\displaystyle {\frac {\pi }{4}}=\arctan(1)=\int _{0}^{\infty }2\exp(-y^{2})\,\mathrm {erf} ^{*}(y)\,\mathrm {d} y={\biggl [}\,\mathrm {erf} ^{*}(y)^{2}{\biggr ]}_{y=0}^{y=\infty }=\lim _{y\rightarrow \infty }\mathrm {erf} ^{*}(y)^{2}} ∫ 0 ∞ exp ( − x 2 ) d x = lim y → ∞ e r f ∗ ( y ) = 1 2 π {\displaystyle \int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x=\lim _{y\rightarrow \infty }\mathrm {erf} ^{*}(y)={\frac {1}{2}}{\sqrt {\pi }}} Mit der genannten Identität des Arkustangens kann somit das Integral der Gaussschen Glockenkurve bewiesen werden.
Auch mit dem Logarithmus Naturalis kann für den Arkustangens eine Integralidentität aufgestellt werden:
arctan ( x ) = ∫ 0 1 1 π y ln [ x 2 + 1 ( y 2 + 1 ) + 2 x y x 2 + 1 ( y 2 + 1 ) − 2 x y ] d y {\displaystyle \arctan(x)=\int _{0}^{1}{\frac {1}{\pi y}}\ln {\biggl [}{\frac {{\sqrt {x^{2}+1}}(y^{2}+1)+2xy}{{\sqrt {x^{2}+1}}(y^{2}+1)-2xy}}{\biggr ]}\,\mathrm {d} y}
Durch Ableiten dieser Integralidentität entsteht ebenso die Ableitung des Arkustangens:
d d x ∫ 0 1 1 π y ln [ x 2 + 1 ( y 2 + 1 ) + 2 x y x 2 + 1 ( y 2 + 1 ) − 2 x y ] d y = ∫ 0 1 4 ( y 2 + 1 ) π x 2 + 1 [ ( x 2 + 1 ) ( y 4 + 1 ) + 2 ( − x 2 + 1 ) y 2 ] d y = 1 x 2 + 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\int _{0}^{1}{\frac {1}{\pi y}}\ln {\biggl [}{\frac {{\sqrt {x^{2}+1}}(y^{2}+1)+2xy}{{\sqrt {x^{2}+1}}(y^{2}+1)-2xy}}{\biggr ]}\,\mathrm {d} y=\int _{0}^{1}{\frac {4(y^{2}+1)}{\pi {\sqrt {x^{2}+1}}{\bigl [}(x^{2}+1)(y^{4}+1)+2(-x^{2}+1)\,y^{2}{\bigr ]}}}\,\mathrm {d} y={\frac {1}{x^{2}+1}}} Die genannte Integralidentität ist bezüglich x eine Ursprungsfunktion.
Die nun gezeigte Integralidentität wurde durch den Mathematiker James Harper entdeckt und in seinem Werk Another simple proof [ 12]
Wenn der Grenzwert von dieser Identität für x → ∞ {\displaystyle x\rightarrow \infty } Areatangens Hyperbolicus folgende Identität:
∫ 0 1 1 y a r t a n h ( y ) d y = π 2 8 {\displaystyle \int _{0}^{1}{\frac {1}{y}}\,\mathrm {artanh} (y)\,\mathrm {d} y={\frac {\pi ^{2}}{8}}} Und mit dieser Formel kann das Basler Problem gelöst werden.
Ebenso kann für das Quadrat des Arkustangens eine Logarithmus-Naturalis-Integralidentität aufgestellt werden:
arctan ( x ) 2 = ∫ 0 1 1 2 z ln [ ( x 2 + 1 ) ( z + 1 ) 2 ( x 2 + 1 ) ( z 2 + 1 ) + 2 ( 1 − x 2 ) z ] d z {\displaystyle \arctan(x)^{2}=\int _{0}^{1}{\frac {1}{2z}}\ln {\biggl [}{\frac {(x^{2}+1)(z+1)^{2}}{(x^{2}+1)(z^{2}+1)+2(1-x^{2})z}}{\biggr ]}\,\mathrm {d} z}
Das sind die direkten Stammfunktionen der beiden behandelten Arkusfunktionen:
Arkustangens:
Die Ursprungsstammfunktion des Arkustangens lautet so:
∫ 0 x arctan ( y ) d y = ∫ 0 1 x arctan ( x z ) d z = x arctan ( x ) − 1 2 ln ( 1 + x 2 ) {\displaystyle \int _{0}^{x}\arctan(y)\,\mathrm {d} y=\int _{0}^{1}x\arctan(xz)\,\mathrm {d} z=x\arctan(x)-{\frac {1}{2}}\ln(1+x^{2})} Nach dem Fundamentalsatz der Infinitesimalrechnung gilt somit:
d d x [ x arctan ( x ) − 1 2 ln ( 1 + x 2 ) ] = arctan ( x ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\biggl [}x\arctan(x)-{\frac {1}{2}}\ln(1+x^{2}){\biggr ]}=\arctan(x)} Arkuskotangens:
Die Ursprungsstammfunktion des Arkuskotangens ist diese Funktion:
∫ 0 x arccot ( y ) d y = ∫ 0 1 x arccot ( x z ) d z = x arccot ( x ) + 1 2 ln ( 1 + x 2 ) {\displaystyle \int _{0}^{x}\operatorname {arccot}(y)\,\mathrm {d} y=\int _{0}^{1}x\operatorname {arccot}(xz)\,\mathrm {d} z=x\operatorname {arccot}(x)+{\frac {1}{2}}\ln(1+x^{2})} Analog zum vorherigen Fall gilt damit:
d d x [ x arccot ( x ) + 1 2 ln ( 1 + x 2 ) ] = arccot ( x ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\biggl [}x\operatorname {arccot}(x)+{\frac {1}{2}}\ln(1+x^{2}){\biggr ]}=\operatorname {arccot}(x)} Von einer ursprünglichen Stammfunktion auf die jeweils andere kann außerdem mit dieser Beziehung direkt gefolgert werden:
arccot ( x ) + arctan ( x ) = π 2 {\displaystyle \operatorname {arccot}(x)+\arctan(x)={\frac {\pi }{2}}}
Stammfunktion des kardinalisierten Arkustangens Der kardinalisierte Arkustangens hat das sogenannte Arkustangensintegral (Inverse Tangent Integral )[ 13]
∫ 0 x 1 y arctan ( y ) d y = ∫ 0 1 1 z arctan ( x z ) d z = Ti 2 ( x ) {\displaystyle \int _{0}^{x}{\frac {1}{y}}\arctan(y)\,\mathrm {d} y=\int _{0}^{1}{\frac {1}{z}}\arctan(xz)\,\mathrm {d} z=\operatorname {Ti} _{2}(x)} Diese Funktion zählt zu den Polylogarithmen und bildet zu der Legendresche Chifunktion χ 2 {\displaystyle \chi _{2}}
Die Catalansche Konstante ist das bekannteste Beispiel für einen Wert dieser Stammfunktion:
∫ 0 1 1 x arctan ( x ) d x = Ti 2 ( 1 ) = β ( 2 ) = G {\displaystyle \int _{0}^{1}{\frac {1}{x}}\arctan(x)\,\mathrm {d} x=\operatorname {Ti} _{2}(1)=\beta (2)=G} Mit dem kleinen Beta wird hierbei die Dirichletsche Betafunktion dargestellt.
Dies sind zwei weitere Funktionswerte für das Arkustangensintegral:
Ti 2 ( 2 − 3 ) = 2 3 G − 1 12 π arcosh ( 2 ) {\displaystyle \operatorname {Ti} _{2}(2-{\sqrt {3}})={\tfrac {2}{3}}G-{\tfrac {1}{12}}\pi \operatorname {arcosh} (2)} Ti 2 ( 2 + 3 ) = 2 3 G + 5 12 π arcosh ( 2 ) {\displaystyle \operatorname {Ti} _{2}(2+{\sqrt {3}})={\tfrac {2}{3}}G+{\tfrac {5}{12}}\pi \operatorname {arcosh} (2)} Diese Bilanz stellt eine Beziehung zur Funktion Areasinus Hyperbolicus her:
Ti 2 ( x 2 + 1 + x ) − Ti 2 ( x 2 + 1 − x ) = 1 2 π arsinh ( x ) {\displaystyle \operatorname {Ti} _{2}({\sqrt {x^{2}+1}}+x)-\operatorname {Ti} _{2}({\sqrt {x^{2}+1}}-x)={\tfrac {1}{2}}\pi \operatorname {arsinh} (x)} Zur Ursprungsstammfunktion des kardinalisierten Arkussinus, dem sogenannten Arkussinusintegral hat das Arkustangensintegral diese Identität:
2 T i 2 [ x ( 1 + 1 − x 2 ) − 1 ] = 4 S i 2 ( 1 2 1 + x − 1 2 1 − x ) − S i 2 ( x ) {\displaystyle 2\,\mathrm {Ti} _{2}{\bigl [}x(1+{\sqrt {1-x^{2}}})^{-1}{\bigr ]}=4\,\mathrm {Si} _{2}{\bigl (}{\tfrac {1}{2}}{\sqrt {1+x}}-{\tfrac {1}{2}}{\sqrt {1-x}}\,{\bigr )}-\mathrm {Si} _{2}(x)}
Summenreihen mit dem Arkustangens Einige Arkustangenssummen divergieren:
∑ n = 1 ∞ arctan ( 1 n ) = + ∞ {\displaystyle \sum _{n=1}^{\infty }\arctan \left({\frac {1}{n}}\right)=+\infty } Vergleichsformel ohne Arkustangens:
∑ n = 1 ∞ 1 n = + ∞ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=+\infty } Andere Arkustangenssummen konvergieren:
∑ n = 1 ∞ arctan ( 1 n 2 ) = π 4 + arctan [ − cot ( 1 2 2 π ) tanh ( 1 2 2 π ) ] ≈ 1,424 74177842998 {\displaystyle \sum _{n=1}^{\infty }\arctan \left({\frac {1}{n^{2}}}\right)={\frac {\pi }{4}}+\arctan \left[-\cot \left({\frac {1}{2}}{\sqrt {2}}\,\pi \right)\tanh \left({\frac {1}{2}}{\sqrt {2}}\,\pi \right)\right]\approx 1{,}42474177842998} Die Abkürzung tanh bringt die Funktion Tangens Hyperbolicus zum Ausdruck.
Vergleichsformel ohne Arkustangens:
∑ n = 1 ∞ 1 n 2 = π 2 6 ≈ 1,644 934066848 {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}\approx 1{,}644934066848} Folgende Formel handelt von den Fibonacci-Zahlen und ergibt ein einfaches Resultat:
∑ n = 1 ∞ arctan ( 1 f 2 n − 1 ) = π 2 ≈ 1,570 7963267948966 {\displaystyle \sum _{n=1}^{\infty }\arctan \left({\frac {1}{f_{2n-1}}}\right)={\frac {\pi }{2}}\approx 1{,}5707963267948966} Denn für alle natürlichen Zahlen n {\displaystyle n} [ 14]
arctan ( 1 f 2 n ) = arctan ( 1 f 2 n + 1 ) + arctan ( 1 f 2 n + 2 ) {\displaystyle \arctan \left({\frac {1}{f_{2n}}}\right)=\arctan \left({\frac {1}{f_{2n+1}}}\right)+\arctan \left({\frac {1}{f_{2n+2}}}\right)} Mit der Tangenssumme ausgedrückt:
1 f 2 n = 1 f 2 n + 1 ⊕ 1 f 2 n + 2 {\displaystyle {\frac {1}{f_{2n}}}={\frac {1}{f_{2n+1}}}\oplus {\frac {1}{f_{2n+2}}}} Dagegen ergibt die Vergleichsformel ohne Arkustangens ein elliptisches[ 15] [ 16]
∑ n = 1 ∞ 1 f 2 n − 1 = 5 8 [ ϑ 00 ( φ ) 2 − ϑ 01 ( φ ) 2 ] ≈ 1,824 5151574 {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{f_{2n-1}}}={\frac {\sqrt {5}}{8}}\left[\vartheta _{00}(\varphi )^{2}-\vartheta _{01}(\varphi )^{2}\right]\approx 1{,}8245151574} φ = 1 2 ( 5 − 1 ) {\displaystyle \varphi ={\frac {1}{2}}\left({\sqrt {5}}-1\right)} Die kleinen griechischen Thetasymbole stellen die Jacobische Thetafunktion dar.
Die Summenreihen mit dem Arkustangens als Summanden dienen auch zur Beschreibung einiger Funktionen. Beispielsweise hat die Gudermannfunktion für alle reellen Zahlen x {\displaystyle x}
gd ( x ) = ∑ n = 1 ∞ { 2 arctan [ 2 x ( 4 n − 3 ) π ] − 2 arctan [ 2 x ( 4 n − 1 ) π ] } {\displaystyle \operatorname {gd} (x)=\sum _{n=1}^{\infty }\left\{2\arctan \left[{\frac {2\,x}{(4n-3)\,\pi }}\right]-2\arctan \left[{\frac {2\,x}{(4n-1)\,\pi }}\right]\right\}} Diese Summenreihe geht als Ursprungsstammfunktion aus der Cauchyschen Summenreihe für den Sekans Hyperbolicus hervor:
sech ( x ) = ∑ n = 1 ∞ [ ( 16 n − 12 ) π ( 4 n − 3 ) 2 π 2 + 4 x 2 − ( 16 n − 4 ) π ( 4 n − 1 ) 2 π 2 + 4 x 2 ] {\displaystyle \operatorname {sech} (x)=\sum _{n=1}^{\infty }\left[{\frac {(16n-12)\,\pi }{(4n-3)^{2}\,\pi ^{2}+4\,x^{2}}}-{\frac {(16n-4)\,\pi }{(4n-1)^{2}\,\pi ^{2}+4\,x^{2}}}\right]}
Siehe auch
Literatur I. N. Bronstein , K. A. Semendjajev , G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik . 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch , Frankfurt am Main 2008, ISBN 978-3-8171-2007-9 , S. 85–88 . G.Huvent: Autour de la primitive de tp coth (αt/2) . 3. Februar 2002. Seite 5 Mircea Ivan: A simple solution to Basel problem . General Mathematics Vol. 16, No. 4, Technical University of Cluj-Napoca Department of Mathematics, 2008 James D. Harper: A simple proof of 1 + 1 / 2 2 + 1 / 3 2 + … = π 2 / 6 {\displaystyle 1+1/2^{2}+1/3^{2}+\ldots =\pi ^{2}/6} The American Mathematical Monthly 109(6) (Jun. – Jul., 2003) 540–541.
Weblinks
Einzelnachweise und Anmerkungen ↑ Beide Funktionen sind monoton in diesen Intervallen, und diese sind von den jeweiligen Polstellen begrenzt. ↑ Eric W. Weisstein : Inverse Tangent .MathWorld ↑ Eric W. Weisstein : Inverse Cotangent .MathWorld ↑ Georg Hoever: Höhere Mathematik kompakt . Springer Spektrum, Berlin Heidelberg 2014, ISBN 978-3-662-43994-4 (eingeschränkte Vorschau in der Google-Buchsuche). ↑ Weitere Approximationen (en) (Memento Internet Archive ↑ Derrick Henry Lehmer: Interesting Series Involving the Central Binomial Coefficient . Volume 92, 1985. Seite 452 ↑ Bspw. sind die Zahlen 1 , 2 , 4 , 5 , … {\displaystyle 1,2,4,5,\dotsc } Størmer-Zahlen ;3 , … , 57 , … , 239 , … , 682 , … , 12943 , … {\displaystyle 3,\dotso ,57,\dotso ,239,\dotso ,682,\dotso ,12943,\dotso } ↑ Dabei ist n ≈ 2,844 38 … ⋅ 10 226 . {\displaystyle n\approx 2{,}84438\dotso \cdot 10^{226}.} ↑ Milton Abramowitz und Irene Stegun : Handbook of Mathematical Functions .ISBN 0-486-61272-4 Formel 4.4.3 (Memento Originals Internet Archive Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1 @2 Vorlage:Webachiv/IABot/www.math.hkbu.edu.hk ↑ Eine ganz ähnliche Skizze ist die von Einheitskreis#Rationale Parametrisierung . ↑ Beim Rechnen mit Gleitkommazahlen besteht Instabilität in der Nähe des − x {\displaystyle -x} | r + x | ≪ 1. {\displaystyle |r+x|\ll 1.} ↑ James D.Harper, Another simple proof of 1 + 1 2 2 + 1 3 2 + ⋯ = π 2 6 {\displaystyle 1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}} , American Mathematical Monthly, Band 110, Nr. 6, 2003, S. 540–541 ↑ Eric W. Weisstein: Inverse Tangent Integral. Abgerufen am 31. Oktober 2023 (englisch). ↑ Fibonacci numbers and the arctangent function - ProQuest. Abgerufen am 4. Dezember 2022 . ↑ Eric W. Weisstein: Reciprocal Fibonacci Constant. Abgerufen am 4. Dezember 2022 (englisch). ↑ Number-theoretical, combinatorial and integer functions — mpmath 1.1.0 documentation. Abgerufen am 4. Dezember 2022 .