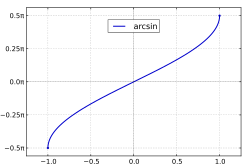
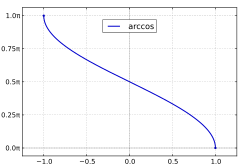
Arkussinus und Arkuskosinus im kartesischen Koordinatensystem arcsin (x ) arccos (x ) Beispiel: Umkehrung der Kosinus- und Sinusfunktion[1] Der Arkussinus – geschrieben arcsin {\displaystyle \arcsin } asin {\displaystyle \operatorname {asin} } Arkuskosinus (oder auch Arkuscosinus ) – geschrieben arccos {\displaystyle \arccos } acos {\displaystyle \operatorname {acos} } Umkehrfunktionen der (geeignet) eingeschränkten Sinus- bzw. Kosinusfunktion . Sinus und Kosinus sind Funktionen, die einen Winkel auf einen Wert im Intervall [ − 1 , 1 ] {\displaystyle [-1,1]} [ − 1 , 1 ] {\displaystyle [-1,1]} [ − 1 , 1 ] {\displaystyle [-1,1]} Definitionsmenge auf das Intervall [ − π 2 , π 2 ] {\displaystyle [-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}]} [ 0 , π ] {\displaystyle [0,\pi ]}
Zusammen mit dem Arkustangens als Umkehrfunktion des (ebenfalls geeignet eingeschränkten) Tangens bilden der Arkussinus und Arkuskosinus den Kern der Klasse der Arkusfunktionen . Aufgrund der in neuerer Zeit für Umkehrfunktionen gebräuchlichen Schreibweise f − 1 {\displaystyle f^{-1}} sin − 1 {\displaystyle \sin ^{-1}} cos − 1 {\displaystyle \cos ^{-1}} arcsin {\displaystyle \arcsin } arccos {\displaystyle \arccos } Kehrwerten des Sinus und Kosinus (Kosekans und Sekans ) führen kann.[2]
Definitionen Die Sinusfunktion ist 2 π {\displaystyle 2\pi } Periode nicht injektiv . Daher muss ihr Definitionsbereich geeignet eingeschränkt werden, um eine umkehrbar-eindeutige Funktion zu erhalten. Da es für diese Einschränkung mehrere Möglichkeiten gibt, spricht man von Zweigen des Arkussinus. Meist wird der Hauptzweig (oder Hauptwert )
arcsin : [ − 1 , 1 ] → [ − π 2 , π 2 ] , {\displaystyle \arcsin \colon [-1,1]\to \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right],} die Umkehrfunktion der Einschränkung sin | [ − π 2 , π 2 ] {\displaystyle \sin |_{\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}} [ − π 2 , π 2 ] , {\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right],}
Analog zum Arkussinus wird der Hauptzweig des Arkuskosinus als die Umkehrfunktion von cos | [ 0 , π ] {\displaystyle \cos |_{[0,\pi ]}}
arccos : [ − 1 , 1 ] → [ 0 , π ] {\displaystyle \arccos \colon [-1,1]\to [0,\pi ]} ebenfalls eine bijektive Funktion. Mittels
arccos ( x ) + arcsin ( x ) = π 2 {\displaystyle \arccos(x)+\arcsin(x)={\frac {\pi }{2}}} lassen sich diese beiden Funktionen ineinander umrechnen.
Eigenschaften Arkussinus Arkuskosinus Funktionsgraph Definitionsmenge [ − 1 , 1 ] {\displaystyle [-1,1]} [ − 1 , 1 ] {\displaystyle [-1,1]} Bildmenge [ − π 2 , π 2 ] {\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]} [ 0 , π ] {\displaystyle [0,\pi ]} Monotonie streng monoton steigend streng monoton fallend Symmetrien Ungerade Funktion (Punktsymmetrie zu ( 0 , 0 ) {\displaystyle (0,0)} arcsin ( − x ) = − arcsin ( x ) {\displaystyle \arcsin(-x)=-\arcsin(x)} Punktsymmetrie zu ( 0 , π 2 ) : {\displaystyle \left(0,{\tfrac {\pi }{2}}\right)\colon } arccos ( x ) = π − arccos ( − x ) {\displaystyle \arccos(x)=\pi -\arccos(-x)} Asymptoten keine keine Nullstellen Eine Nullstelle bei x = 0 {\displaystyle x=0} Eine Nullstelle bei x = 1 {\displaystyle x=1} Sprungstellen keine keine Polstellen keine keine Extrema Globales Maximum π 2 {\displaystyle {\tfrac {\pi }{2}}} 1 {\displaystyle 1} − π 2 {\displaystyle -{\tfrac {\pi }{2}}} − 1 {\displaystyle -1} Globales Maximum π {\displaystyle \pi } − 1 {\displaystyle -1} 0 {\displaystyle 0} 1 {\displaystyle 1} Wendepunkte ( 0 , 0 ) {\displaystyle (0,0)} ( 0 , π 2 ) {\displaystyle \left(0,{\frac {\pi }{2}}\right)}
Aufgrund der Symmetrieeigenschaften gilt:
arcsin ( − x ) = − arcsin ( x ) {\displaystyle \arcsin(-x)=-\arcsin(x)} arccos ( − x ) = π − arccos ( x ) {\displaystyle \arccos(-x)=\pi -\arccos(x)}
Reihenentwicklungen Die Taylorreihe des Arkussinus erhält man durch Entwickeln der Ableitung in eine binomische Reihe und anschließende Integration, sie ist gegeben durch:
arcsin ( x ) = ∑ k = 0 ∞ ( 2 k − 1 ) ! ! ( 2 k ) ! ! x 2 k + 1 2 k + 1 = ∑ k = 0 ∞ ( 2 k k ) x 2 k + 1 4 k ( 2 k + 1 ) = ∑ k = 0 ∞ CBC ( k ) 4 k ( 2 k + 1 ) x 2 k + 1 = = x + 1 2 ⋅ x 3 3 + 1 ⋅ 3 2 ⋅ 4 ⋅ x 5 5 + 1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6 ⋅ x 7 7 + ⋯ {\displaystyle {\begin{aligned}\arcsin(x)&=\sum _{k=0}^{\infty }{\frac {(2k-1)!!}{(2k)!!}}{\frac {x^{2k+1}}{2k+1}}=\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {x^{2k+1}}{4^{k}(2k+1)}}=\sum _{k=0}^{\infty }\,{\frac {\operatorname {CBC} (k)}{4^{k}(2k+1)}}\,x^{2k+1}=\\&={x+{\frac {1}{2}}\cdot {\frac {x^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}\cdot {\frac {x^{5}}{5}}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\cdot {\frac {x^{7}}{7}}+\dotsb }\end{aligned}}} Die Taylorreihe des Arkuskosinus ergibt sich aus der Beziehung arccos x = π 2 − arcsin x {\displaystyle \arccos x={\tfrac {\pi }{2}}-\arcsin x}
arccos ( x ) = π 2 − ∑ k = 0 ∞ ( 2 k − 1 ) ! ! ( 2 k ) ! ! x 2 k + 1 2 k + 1 = π 2 − ∑ k = 0 ∞ ( 2 k k ) x 2 k + 1 4 k ( 2 k + 1 ) {\displaystyle \arccos(x)={\frac {\pi }{2}}-\sum _{k=0}^{\infty }{\frac {(2k-1)!!}{(2k)!!}}{\frac {x^{2k+1}}{2k+1}}={\frac {\pi }{2}}-\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {x^{2k+1}}{4^{k}(2k+1)}}} Beide Reihen haben den Konvergenzradius 1.
Der Ausdruck k ! ! {\displaystyle k!!} Doppelfakultät und mit dem Ausdruck CBC wird der Zentralbinomialkoeffizient bezeichnet:
CBC ( x ) = ( 2 x x ) = ( 2 x ) ! ( x ! ) 2 = Π ( 2 x ) Π ( x ) 2 = ∏ n = 1 ∞ [ ( 1 + x n ) 2 ( 1 + 2 x n ) − 1 ] {\displaystyle \operatorname {CBC} (x)={2x \choose x}={\frac {(2x)!}{(x!)^{2}}}={\frac {\Pi (2x)}{\Pi (x)^{2}}}=\prod _{n=1}^{\infty }{\bigl [}{\bigl (}1+{\frac {x}{n}}{\bigr )}^{2}{\bigl (}1+{\frac {2x}{n}}{\bigr )}^{-1}{\bigr ]}} So wird der Zentralbinomialkoeffizient mit Hilfe von der Fakultätsfunktion beziehungsweise der Gaußschen Pifunktion definiert.
Im Gegensatz zum Arkussinus selbst hat das Quadrat des Arkussinus in dessen MacLaurinschen Reihe den Zentralbinomialkoeffizienten [3]
arcsin ( x ) 2 = ∑ n = 1 ∞ 2 2 n − 1 n 2 CBC ( n ) x 2 n = = x 2 + 1 3 ⋅ x 4 + 8 45 ⋅ x 6 + 4 35 ⋅ x 8 + ⋯ {\displaystyle {\begin{aligned}\arcsin(x)^{2}&=\sum _{n=1}^{\infty }\,{\frac {2^{2n-1}}{n^{2}\operatorname {CBC} (n)}}\,x^{2n}=\\&={x^{2}+{\frac {1}{3}}\cdot x^{4}+{\frac {8}{45}}\cdot x^{6}+{\frac {4}{35}}\cdot x^{8}+\dotsb }\end{aligned}}} Das Gleiche gilt somit auch für den Quotienten aus Arkussinus und Pythagoräischer Gegenstückfunktion:
arcsin ( x ) 1 − x 2 = ∑ n = 1 ∞ 2 2 n − 1 n CBC ( n ) x 2 n − 1 = x + 2 3 ⋅ x 3 + 8 15 ⋅ x 5 + 16 35 ⋅ x 7 + ⋯ {\displaystyle {\begin{aligned}{\frac {\arcsin(x)}{\sqrt {1-x^{2}}}}&=\sum _{n=1}^{\infty }\,{\frac {2^{2n-1}}{n\operatorname {CBC} (n)}}\,x^{2n-1}\\&={x+{\frac {2}{3}}\cdot x^{3}+{\frac {8}{15}}\cdot x^{5}+{\frac {16}{35}}\cdot x^{7}+\dotsb }\end{aligned}}}
Verkettungen mit Sinus und Kosinus Für die Arkusfunktionen gelten unter anderem folgende Formeln:
sin ( arccos ( x ) ) = 1 − x 2 {\displaystyle \sin(\arccos(x))={\sqrt {1-x^{2}}}} y = arccos ( x ) {\displaystyle y=\arccos(x)} y ∈ [ 0 , π ] {\displaystyle y\in \left[0,{\pi }\right]} sin ( y ) = 1 − cos 2 ( y ) {\displaystyle \sin(y)={\sqrt {1-\cos ^{2}(y)}}} cos ( arcsin ( x ) ) = 1 − x 2 {\displaystyle \cos(\arcsin(x))={\sqrt {1-x^{2}}}} y = arcsin ( x ) {\displaystyle y=\arcsin(x)} y ∈ [ − π 2 , π 2 ] {\displaystyle y\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]} cos ( y ) = 1 − sin 2 ( y ) {\displaystyle \cos(y)={\sqrt {1-\sin ^{2}(y)}}} sin ( arctan ( x ) ) = x 1 + x 2 {\displaystyle \sin(\arctan(x))={\frac {x}{\sqrt {1+x^{2}}}}} y = arctan ( x ) {\displaystyle y=\arctan(x)} y ∈ ] − π 2 , π 2 [ {\displaystyle y\in \left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[} sin ( y ) = tan ( y ) 1 + tan 2 ( y ) {\displaystyle \sin(y)={\frac {\tan(y)}{\sqrt {1+\tan ^{2}(y)}}}} cos ( arctan ( x ) ) = 1 1 + x 2 {\displaystyle \cos(\arctan(x))={\frac {1}{\sqrt {1+x^{2}}}}} y = arctan ( x ) {\displaystyle y=\arctan(x)} y ∈ ] − π 2 , π 2 [ {\displaystyle y\in \left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[} cos ( y ) = 1 1 + tan 2 ( y ) {\displaystyle \cos(y)={\frac {1}{\sqrt {1+\tan ^{2}(y)}}}}
Beziehung zum Arkustangens Von besonderer Bedeutung in älteren Programmiersprachen ohne implementierte Arkussinus- und Arkuskosinusfunktion sind folgende Beziehungen, die es ermöglichen, den Arkussinus und Arkuskosinus aus dem vielleicht implementierten Arkustangens zu berechnen. Aufgrund obiger Formeln gilt
arcsin ( x ) = arctan ( x 1 − x 2 ) {\displaystyle \arcsin(x)=\arctan \left({\frac {x}{\sqrt {1-x^{2}}}}\right)} arccos ( x ) = π 2 − arctan ( x 1 − x 2 ) {\displaystyle \arccos(x)={\frac {\pi }{2}}-\arctan \left({\frac {x}{\sqrt {1-x^{2}}}}\right)} für | x | < 1. {\displaystyle |x|<1.} arctan ( 1 0 ) := lim t → ∞ arctan ( t ) = π 2 , {\displaystyle \arctan \left({\tfrac {1}{0}}\right):=\lim _{t\to \infty }\arctan(t)={\tfrac {\pi }{2}},} x = ± 1 {\displaystyle x=\pm 1}
arcsin ( x ) = 2 arctan ( x 1 + 1 − x 2 ) {\displaystyle \arcsin(x)=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)} arccos ( x ) = π 2 − 2 arctan ( x 1 + 1 − x 2 ) {\displaystyle \arccos(x)={\frac {\pi }{2}}-2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)} verwenden, was sich aus Obigem durch Anwenden der Funktionalgleichung des Arkustangens ergibt und für | x | ≤ 1 {\displaystyle |x|\leq 1} − 1 < x ≤ 1 {\displaystyle -1<x\leq 1}
arccos ( x ) = 2 arctan ( 1 − x 1 + x ) {\displaystyle \arccos(x)=2\arctan \left({\sqrt {\frac {1-x}{1+x}}}\right)} vereinfachen.
Additionstheoreme Die Additionstheoreme für Arkussinus und Arkuskosinus erhält man mit Hilfe der Additionstheoreme für Sinus und Kosinus :
arcsin x + arcsin y = { arcsin ( sin ( arcsin x + arcsin y ) ) = arcsin ( x 1 − y 2 + y 1 − x 2 ) wenn x y ≤ 0 oder x 2 + y 2 ≤ 1 π − arcsin ( sin ( arcsin x + arcsin y ) ) = π − arcsin ( x 1 − y 2 + y 1 − x 2 ) wenn x > 0 und y > 0 und x 2 + y 2 > 1 − π − arcsin ( sin ( arcsin x + arcsin y ) ) = − π − arcsin ( x 1 − y 2 + y 1 − x 2 ) wenn x < 0 und y < 0 und x 2 + y 2 > 1 {\displaystyle \arcsin x+\arcsin y=\left\{{\begin{array}{rcrl}\arcsin(\sin(\arcsin x+\arcsin y))&=&\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn}}\quad xy\leq 0\quad {\text{oder}}\quad x^{2}+y^{2}\leq 1\\\pi -\arcsin(\sin(\arcsin x+\arcsin y))&=&\pi -\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn}}\quad x>0\quad {\text{und}}\quad y>0\quad {\text{und}}\quad x^{2}+y^{2}>1\\-\pi -\arcsin(\sin(\arcsin x+\arcsin y))&=&-\pi -\arcsin \left(x{\sqrt {1-y^{2}}}+y{\sqrt {1-x^{2}}}\right)&{\text{wenn}}\quad x<0\quad {\text{und}}\quad y<0\quad {\text{und}}\quad x^{2}+y^{2}>1\\\end{array}}\right.} arccos x + arccos y = { arccos ( cos ( arccos x + arccos y ) ) = arccos ( x y − 1 − x 2 1 − y 2 ) wenn x + y ≥ 0 2 π − arccos ( cos ( arccos x + arccos y ) ) = 2 π − arccos ( x y − 1 − x 2 1 − y 2 ) wenn x + y < 0 {\displaystyle \arccos x+\arccos y=\left\{{\begin{array}{rcrl}\arccos(\cos(\arccos x+\arccos y))&=&\arccos \left(xy-{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)&{\text{wenn}}\quad x+y\geq 0\\2\pi -\arccos(\cos(\arccos x+\arccos y))&=&2\pi -\arccos \left(xy-{\sqrt {1-x^{2}}}{\sqrt {1-y^{2}}}\right)&{\text{wenn}}\quad x+y<0\\\end{array}}\right.} Daraus folgt insbesondere für doppelte Funktionswerte
2 arcsin x = { arcsin ( 2 x 1 − x 2 ) wenn 2 x 2 ≤ 1 π − arcsin ( 2 x 1 − x 2 ) wenn x > 0 und 2 x 2 > 1 − π − arcsin ( 2 x 1 − x 2 ) wenn x < 0 und 2 x 2 > 1 {\displaystyle 2\arcsin x=\left\{{\begin{array}{rl}\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn}}\quad 2x^{2}\leq 1\\\pi -\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn}}\quad x>0\quad {\text{und}}\quad 2x^{2}>1\\-\pi -\arcsin \left(2x{\sqrt {1-x^{2}}}\right)&{\text{wenn}}\quad x<0\quad {\text{und}}\quad 2x^{2}>1\\\end{array}}\right.} 2 arccos x = { arccos ( 2 x 2 − 1 ) wenn x ≥ 0 2 π − arccos ( 2 x 2 − 1 ) wenn x < 0 {\displaystyle 2\arccos x=\left\{{\begin{array}{rl}\arccos \left(2x^{2}-1\right)&{\text{wenn}}\quad x\geq 0\\2\pi -\arccos \left(2x^{2}-1\right)&{\text{wenn}}\quad x<0\\\end{array}}\right.}
Ableitungen Arkussinus d d x arcsin ( x ) = 1 1 − x 2 , − 1 < x < 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1} Arkuskosinus d d x arccos ( x ) = − 1 1 − x 2 , − 1 < x < 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1} Umrechnung d d x arccos ( x ) = − d d x arcsin ( x ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\arccos(x)=-{\frac {\mathrm {d} }{\mathrm {d} x}}\arcsin(x)}
Integrale
Standardisierte Integraldarstellungen Die Integraldarstellungen des Arkussinus bzw. Arkuskosinus sind gegeben durch:
arcsin ( x ) = ∫ 0 x d t 1 − t 2 = ∫ 0 1 x 1 − x 2 y 2 d y {\displaystyle \arcsin(x)=\int \limits _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}=\int \limits _{0}^{1}{\frac {x}{\sqrt {1-x^{2}y^{2}}}}\,\mathrm {d} y} arccos ( x ) = ∫ x 1 d t 1 − t 2 = π 2 − ∫ 0 1 x 1 − x 2 y 2 d y {\displaystyle \arccos(x)=\int \limits _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}={\frac {\pi }{2}}-\int \limits _{0}^{1}{\frac {x}{\sqrt {1-x^{2}y^{2}}}}\,\mathrm {d} y}
Auch mit dem Logarithmus Naturalis kann für den Arkussinus eine Integralidentität aufgestellt werden:
1 1 − x 2 = ∫ 0 1 4 ( y 2 + 1 ) π [ ( y 2 + 1 ) 2 − 4 x 2 y 2 ] d y {\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}=\int \limits _{0}^{1}{\frac {4\,(y^{2}+1)}{\pi {\bigl [}(y^{2}+1)^{2}-4\,x^{2}y^{2}{\bigr ]}}}\,\mathrm {d} y} Durch Bildung der Ursprungsstammfunktion bezüglich x entsteht folgende Formel:
arcsin ( x ) = ∫ 0 1 1 π y ln ( y 2 + 2 x y + 1 y 2 − 2 x y + 1 ) d y {\displaystyle \arcsin(x)=\int \limits _{0}^{1}{\frac {1}{\pi \,y}}\ln {\biggl (}{\frac {y^{2}+2xy+1}{y^{2}-2xy+1}}{\biggr )}\,\mathrm {d} y}
Die nun gezeigte Integralidentität wurde durch den Mathematiker James Harper entdeckt und in seinen Werken A simple proof of 1 + 1 / 2 2 + 1 / 3 2 + … = π 2 / 6 {\displaystyle 1+1/2^{2}+1/3^{2}+\ldots =\pi ^{2}/6} und Another simple proof of 1 + 1 / 2 2 + 1 / 3 2 + … = π 2 / 6 {\displaystyle 1+1/2^{2}+1/3^{2}+\ldots =\pi ^{2}/6} [4] Basler Problem und konnte einige weitere Integralidentitäten aufstellen, welche das Bindeglied zwischen den Arkusfunktionen und den Areafunktionen beziehungsweise Logarithmusfunktionen darstellen. Beispielsweise gilt folgendes Integral:
∫ 0 1 1 y ln ( y 2 + y + 1 y 2 − y + 1 ) d y = π 2 6 {\displaystyle \int \limits _{0}^{1}{\frac {1}{y}}\ln {\biggl (}{\frac {y^{2}+y+1}{y^{2}-y+1}}{\biggr )}\,\mathrm {d} y={\frac {\pi ^{2}}{6}}} Eine analoge Integralidentität nach demselben Grundmuster kann für das Quadrat des Arkuskosinus hervorgebracht werden:
arccos ( x ) 2 = π 2 3 − ∫ 0 1 2 y ln ( y 2 + 2 x y + 1 ) d y {\displaystyle \arccos(x)^{2}={\frac {\pi ^{2}}{3}}-\int \limits _{0}^{1}{\frac {2}{y}}\ln(y^{2}+2xy+1)\,\mathrm {d} y}
Und mit dem Areatangens Hyperbolicus kann für den Arkussinus eine Integralidentität aufgestellt werden:
2 arcsin ( x ) 1 − x 2 = ∫ 0 1 2 x ( 1 − x 2 ) ( 1 − x 2 y 2 ) d y {\displaystyle {\frac {2\arcsin(x)}{\sqrt {1-x^{2}}}}=\int \limits _{0}^{1}{\frac {2\,x}{\sqrt {(1-x^{2})(1-x^{2}y^{2})}}}\,\mathrm {d} y} Durch Bildung der Ursprungsstammfunktion bezüglich x entsteht folgende Formel:
arcsin ( x ) 2 = ∫ 0 1 2 y [ artanh ( y ) − artanh ( 1 − x 2 y 1 − x 2 y 2 ) ] d y {\displaystyle \arcsin(x)^{2}=\int \limits _{0}^{1}{\frac {2}{y}}{\biggl [}\operatorname {artanh} {\bigl (}y{\bigr )}-\operatorname {artanh} {\biggl (}{\frac {{\sqrt {1-x^{2}}}\,y}{\sqrt {1-x^{2}y^{2}}}}{\biggr )}{\biggr ]}\,\mathrm {d} y}
Wenn der Grenzwert von dieser Identität für x = 1 {\displaystyle x=1} Areatangens Hyperbolicus folgende Identität:
∫ 0 1 1 y a r t a n h ( y ) d y = π 2 8 {\displaystyle \int \limits _{0}^{1}{\frac {1}{y}}\,\mathrm {artanh} (y)\,\mathrm {d} y={\frac {\pi ^{2}}{8}}} Und mit dieser Formel kann das Basler Problem bewiesen werden:
∫ 0 1 1 y a r t a n h ( y ) d y = ∫ 0 1 ( 1 y ∑ n = 1 ∞ 1 2 n − 1 y 2 n − 1 ) d y = ∑ n = 1 ∞ 1 ( 2 n − 1 ) 2 {\displaystyle \int \limits _{0}^{1}{\frac {1}{y}}\,\mathrm {artanh} (y)\,\mathrm {d} y=\int \limits _{0}^{1}{\biggl (}{\frac {1}{y}}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\,y^{2n-1}{\biggr )}\,\mathrm {d} y=\sum _{n=1}^{\infty }{\frac {1}{(2n-1)^{2}}}} Daraus folgt:
∑ n = 1 ∞ 1 ( 2 n − 1 ) 2 = π 2 8 {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{(2n-1)^{2}}}={\frac {\pi ^{2}}{8}}}
Stammfunktionen von Arkussinus und Arkuskosinus Arkussinus ∫ arcsin ( x a ) d x = x arcsin ( x a ) + a 2 − x 2 + C {\displaystyle \int \arcsin \left({\frac {x}{a}}\right)\,\mathrm {d} x=x\,\arcsin \left({\frac {x}{a}}\right)+{\sqrt {a^{2}-x^{2}}}+C} Arkuskosinus ∫ arccos ( x a ) d x = x arccos ( x a ) − a 2 − x 2 + C {\displaystyle \int \arccos \left({\frac {x}{a}}\right)\,\mathrm {d} x=x\,\arccos \left({\frac {x}{a}}\right)-{\sqrt {a^{2}-x^{2}}}+C}
Stammfunktion des kardinalisierten Arkussinus Wenn der Arkussinus durch die identische Abbildungsfunktion geteilt wird, dann stellt diese Funktion den kardinalisierten Arkussinus dar.
Die ursprüngliche Stammfunktion des kardinalisierten Arkussinus ist das sogenannte Arkussinusintegral und dies ist eine nicht elemenare Funktion:
∫ 0 x 1 y arcsin ( y ) d y = ∫ 0 1 1 z arcsin ( x z ) d z = Si 2 ( x ) {\displaystyle \int \limits _{0}^{x}{\frac {1}{y}}\arcsin(y)\,\mathrm {d} y=\int _{0}^{1}{\frac {1}{z}}\arcsin(xz)\,\mathrm {d} z=\operatorname {Si} _{2}(x)} Nach dem Fundamentalsatz der Infinitesimalrechnung gilt somit:
d d x Si 2 ( x ) = 1 x arcsin ( x ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {Si} _{2}(x)={\frac {1}{x}}\arcsin(x)} ∫ 0 1 1 x arcsin ( x ) d x = Si 2 ( 1 ) = π 2 ln ( 2 ) {\displaystyle \int \limits _{0}^{1}{\frac {1}{x}}\arcsin(x)\,\mathrm {d} x=\operatorname {Si} _{2}(1)={\frac {\pi }{2}}\ln(2)} Mit dem Satz von Fubini kann der nun genannte Wert des Integrals bewiesen werden:
Si 2 ( 1 ) = ∫ 0 1 1 x arcsin ( x ) d x = ∫ 0 1 ∫ 0 1 1 − x 2 y ( 1 − x 2 y 2 ) 1 − y 2 d y d x = {\displaystyle \operatorname {Si} _{2}(1)=\int \limits _{0}^{1}{\frac {1}{x}}\arcsin(x)\,\mathrm {d} x=\int \limits _{0}^{1}\int \limits _{0}^{1}{\frac {{\sqrt {1-x^{2}}}\,y}{(1-x^{2}y^{2}){\sqrt {1-y^{2}}}}}\,\mathrm {d} y\,\mathrm {d} x=} = ∫ 0 1 ∫ 0 1 1 − x 2 y ( 1 − x 2 y 2 ) 1 − y 2 d x d y = ∫ 0 1 π y 2 1 − y 2 ( 1 + 1 − y 2 ) d y = π 2 ln ( 2 ) {\displaystyle =\int \limits _{0}^{1}\int \limits _{0}^{1}{\frac {{\sqrt {1-x^{2}}}\,y}{(1-x^{2}y^{2}){\sqrt {1-y^{2}}}}}\,\mathrm {d} x\,\mathrm {d} y=\int \limits _{0}^{1}{\frac {\pi \,y}{2{\sqrt {1-y^{2}}}(1+{\sqrt {1-y^{2}}}\,)}}\,\mathrm {d} y={\frac {\pi }{2}}\ln(2)} Mit diesem Arkussinusintegral kann ebenso das sogenannte Arkustangensintegral direkt erzeugt werden:
2 T i 2 [ x ( 1 + 1 − x 2 ) − 1 ] = 4 S i 2 ( 1 2 1 + x − 1 2 1 − x ) − S i 2 ( x ) {\displaystyle 2\,\mathrm {Ti} _{2}{\bigl [}x(1+{\sqrt {1-x^{2}}})^{-1}{\bigr ]}=4\,\mathrm {Si} _{2}{\bigl (}{\tfrac {1}{2}}{\sqrt {1+x}}-{\tfrac {1}{2}}{\sqrt {1-x}}\,{\bigr )}-\mathrm {Si} _{2}(x)}
Komplexe Argumente arcsin ( a + b i ) = s g n + a 2 ⋅ arccos ( ( a 2 + b 2 − 1 ) 2 + 4 b 2 − ( a 2 + b 2 ) ) + i ⋅ s g n + b 2 ⋅ arcosh ( ( a 2 + b 2 − 1 ) 2 + 4 b 2 + ( a 2 + b 2 ) ) {\displaystyle {\begin{aligned}\arcsin(a+b\,\mathrm {i} )=\quad {\frac {\operatorname {sgn^{+}} {a}}{2}}\cdot \arccos &\left({\sqrt {(a^{2}+b^{2}-1)^{2}+4b^{2}}}-(a^{2}+b^{2})\right)\\+\;\mathrm {i} \cdot {\frac {\operatorname {sgn^{+}} {b}}{2}}\cdot \operatorname {arcosh} &\left({\sqrt {(a^{2}+b^{2}-1)^{2}+4b^{2}}}+(a^{2}+b^{2})\right)\end{aligned}}} a , b ∈ R {\displaystyle a,b\in \mathbb {R} } arccos ( a + b i ) = π 2 − arcsin ( a + b i ) {\displaystyle \arccos(a+b\,\mathrm {i} )={\frac {\pi }{2}}-\arcsin(a+b\,\mathrm {i} )} Zur Funktion arcosh {\displaystyle \operatorname {arcosh} } Areakosinus hyperbolicus , und für die Funktion s g n + : R → { − 1 , 1 } {\displaystyle \operatorname {sgn^{+}} \colon \mathbb {R} \to \{-1,1\}}
s g n + ( x ) := 2 ⋅ Θ ( x ) − 1 = { + 1 für x ≥ 0 − 1 für x < 0 {\displaystyle \operatorname {sgn^{+}} (x):=2\cdot \Theta (x)-1={\begin{cases}+1&{\text{für }}x\geq 0\\-1&{\text{für }}x<0\end{cases}}} mit der Heaviside-Funktion Θ {\displaystyle \Theta }
Anmerkungen
Wichtige Funktionswerte Siehe auch: Sinus und Kosinus: Wichtige Funktionswerte
Die folgende Tabelle listet die wichtigen Funktionswerte der beiden Arkusfunktionen auf.[5]
x {\displaystyle x} arcsin ( x ) {\displaystyle \arcsin(x)} arccos ( x ) {\displaystyle \arccos(x)} 0 {\displaystyle 0} 0 ∘ {\displaystyle 0^{\circ }} 0 {\displaystyle 0} 90 ∘ {\displaystyle 90^{\circ }} π 2 {\displaystyle {\frac {\pi }{2}}} 1 2 {\displaystyle {\frac {1}{2}}} 30 ∘ {\displaystyle 30^{\circ }} π 6 {\displaystyle {\frac {\pi }{6}}} 60 ∘ {\displaystyle 60^{\circ }} π 3 {\displaystyle {\frac {\pi }{3}}} 1 2 2 {\displaystyle {\frac {1}{2}}{\sqrt {2}}} 45 ∘ {\displaystyle 45^{\circ }} π 4 {\displaystyle {\frac {\pi }{4}}} 45 ∘ {\displaystyle 45^{\circ }} π 4 {\displaystyle {\frac {\pi }{4}}} 1 2 3 {\displaystyle {\frac {1}{2}}{\sqrt {3}}} 60 ∘ {\displaystyle 60^{\circ }} π 3 {\displaystyle {\frac {\pi }{3}}} 30 ∘ {\displaystyle 30^{\circ }} π 6 {\displaystyle {\frac {\pi }{6}}} 1 {\displaystyle 1} 90 ∘ {\displaystyle 90^{\circ }} π 2 {\displaystyle {\frac {\pi }{2}}} 0 ∘ {\displaystyle 0^{\circ }} 0 {\displaystyle 0}
Weitere wichtige Werte sind:
x {\displaystyle x} arcsin ( x ) {\displaystyle \arcsin(x)} arccos ( x ) {\displaystyle \arccos(x)} 1 4 ( 6 − 2 ) {\displaystyle {\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})} 15 ∘ {\displaystyle 15^{\circ }} π 12 {\displaystyle {\tfrac {\pi }{12}}} 75 ∘ {\displaystyle 75^{\circ }} 5 π 12 {\displaystyle {\tfrac {5\pi }{12}}} 1 4 ( 5 − 1 ) {\displaystyle {\tfrac {1}{4}}\left({\sqrt {5}}-1\right)} 18 ∘ {\displaystyle 18^{\circ }} π 10 {\displaystyle {\tfrac {\pi }{10}}} 72 ∘ {\displaystyle 72^{\circ }} 2 π 5 {\displaystyle {\tfrac {2\pi }{5}}} 1 4 10 − 2 5 {\displaystyle {\tfrac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}} 36 ∘ {\displaystyle 36^{\circ }} π 5 {\displaystyle {\tfrac {\pi }{5}}} 54 ∘ {\displaystyle 54^{\circ }} 3 π 10 {\displaystyle {\tfrac {3\pi }{10}}} 1 4 ( 1 + 5 ) {\displaystyle {\tfrac {1}{4}}\left(1+{\sqrt {5}}\right)} 54 ∘ {\displaystyle 54^{\circ }} 3 π 10 {\displaystyle {\tfrac {3\pi }{10}}} 36 ∘ {\displaystyle 36^{\circ }} π 5 {\displaystyle {\tfrac {\pi }{5}}} 1 4 10 + 2 5 {\displaystyle {\tfrac {1}{4}}{\sqrt {10+2{\sqrt {5}}}}} 72 ∘ {\displaystyle 72^{\circ }} 2 π 5 {\displaystyle {\tfrac {2\pi }{5}}} 18 ∘ {\displaystyle 18^{\circ }} π 10 {\displaystyle {\tfrac {\pi }{10}}} 1 4 ( 6 + 2 ) {\displaystyle {\tfrac {1}{4}}({\sqrt {6}}+{\sqrt {2}})} 75 ∘ {\displaystyle 75^{\circ }} 5 π 12 {\displaystyle {\tfrac {5\pi }{12}}} 15 ∘ {\displaystyle 15^{\circ }} π 12 {\displaystyle {\tfrac {\pi }{12}}}
Kettenbruchdarstellung des Arkussinus H. S. Wall fand 1948 für den Arkussinus folgende Darstellung als Kettenbruch :
arcsin ( x ) = x 1 − x 2 1 − 1 ⋅ 2 x 2 3 − 1 ⋅ 2 x 2 5 − 3 ⋅ 4 x 2 7 − 3 ⋅ 4 x 2 9 − 5 ⋅ 6 x 2 11 − … {\displaystyle \arcsin(x)={\frac {x{\sqrt {1-x^{2}}}}{1-{\cfrac {1\cdot 2x^{2}}{3-{\cfrac {1\cdot 2x^{2}}{5-{\cfrac {3\cdot 4x^{2}}{7-{\cfrac {3\cdot 4x^{2}}{9-{\cfrac {5\cdot 6x^{2}}{11-\ldots }}}}}}}}}}}}}
Komplexe Funktion Man kann Arkussinus und Arkuskosinus auch durch den Hauptzweig des komplexen Logarithmus ausdrücken:
arcsin z = − i ln ( i z + 1 − z 2 ) {\displaystyle \arcsin z=-\mathrm {i} \,\ln \left(\mathrm {i} z+{\sqrt {1-z^{2}}}\right)} arccos z = − i ln ( z + i 1 − z 2 ) {\displaystyle \arccos z=-\mathrm {i} \,\ln \left(z+\mathrm {i} {\sqrt {1-z^{2}}}\right)} Diese beiden Formeln kann man wie folgt herleiten:
Für arcsin z {\displaystyle \arcsin z}
sin ( x ) = e i x − e − i x 2 i e i x − e − i x 2 i = z e i x − 1 e i x = 2 z i ( e i x ) 2 − 1 = 2 z i e i x ( e i x ) 2 − 2 z i e i x − 1 = 0 e i x = − − 2 z i 2 ± ( − 2 z i 2 ) 2 − ( − 1 ) e i x = z i ± 1 − z 2 i x = ln ( z i ± 1 − z 2 ) x = ln ( z i ± 1 − z 2 ) i x = ln ( z i ± 1 − z 2 ) i i 2 x = ln ( z i ± 1 − z 2 ) i − 1 x = − i ln ( z i ± 1 − z 2 ) arcsin z = − i ln ( z i ± 1 − z 2 ) {\displaystyle {\begin{aligned}\sin(x)&={\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2\mathrm {i} }}\\{\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2\mathrm {i} }}&=z\\\mathrm {e} ^{\mathrm {i} x}-{\frac {1}{\mathrm {e} ^{\mathrm {i} x}}}&=2z\mathrm {i} \\(\mathrm {e} ^{\mathrm {i} x})^{2}-1&=2z\mathrm {i} \mathrm {e} ^{\mathrm {i} x}\\(\mathrm {e} ^{\mathrm {i} x})^{2}-2z\mathrm {i} \mathrm {e} ^{\mathrm {i} x}-1&=0\\\mathrm {e} ^{\mathrm {i} x}&=-{\frac {-2z\mathrm {i} }{2}}\pm {\sqrt {\left({\frac {-2z\mathrm {i} }{2}}\right)^{2}-(-1)}}\\\mathrm {e} ^{\mathrm {i} x}&=z\mathrm {i} \pm {\sqrt {1-z^{2}}}\\\mathrm {i} x&=\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\x&={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})}{\mathrm {i} }}\\x&={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\,\mathrm {i} }{\mathrm {i} ^{2}}}\\x&={\frac {\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\,\mathrm {i} }{-1}}\\x&=-\mathrm {i} \,\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\\arcsin z&=-\mathrm {i} \,\ln(z\mathrm {i} \pm {\sqrt {1-z^{2}}})\\\end{aligned}}} Für arccos z {\displaystyle \arccos z}
cos ( x ) = e i x + e − i x 2 e i x + e − i x 2 = z e i x + 1 e i x = 2 z ( e i x ) 2 + 1 = 2 z e i x ( e i x ) 2 − 2 z e i x + 1 = 0 e i x = − − 2 z 2 ± ( − 2 z 2 ) 2 − 1 ) e i x = z ± z 2 − 1 i x = ln ( z ± i 1 − z 2 ) x = ln ( z ± i 1 − z 2 ) i x = ln ( z ± i 1 − z 2 ) i i 2 x = ln ( z ± i 1 − z 2 ) i − 1 x = − i ln ( z ± i 1 − z 2 ) arccos z = − i ln ( z ± i 1 − z 2 ) {\displaystyle {\begin{aligned}\cos(x)&={\frac {\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}}{2}}\\{\frac {\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}}{2}}&=z\\\mathrm {e} ^{\mathrm {i} x}+{\frac {1}{\mathrm {e} ^{\mathrm {i} x}}}&=2z\\(\mathrm {e} ^{\mathrm {i} x})^{2}+1&=2z\mathrm {e} ^{\mathrm {i} x}\\(\mathrm {e} ^{\mathrm {i} x})^{2}-2z\mathrm {e} ^{\mathrm {i} x}+1&=0\\\mathrm {e} ^{\mathrm {i} x}&=-{\frac {-2z}{2}}\pm {\sqrt {\left({\frac {-2z}{2}}\right)^{2}-1)}}\\\mathrm {e} ^{\mathrm {i} x}&=z\pm {\sqrt {z^{2}-1}}\\\mathrm {i} x&=\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\x&={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})}{\mathrm {i} }}\\x&={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\,\mathrm {i} }{\mathrm {i} ^{2}}}\\x&={\frac {\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\,\mathrm {i} }{-1}}\\x&=-\mathrm {i} \,\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\\arccos z&=-\mathrm {i} \,\ln(z\pm \mathrm {i} {\sqrt {1-z^{2}}})\\\end{aligned}}}
Siehe auch
Literatur I. N. Bronstein , K. A. Semendjajev , G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik . 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch , Frankfurt am Main 2008, ISBN 978-3-8171-2007-9 , S. 85–88 . G.Huvent: Autour de la primitive de tp coth (αt/2) . 3. Februar 2002. Seite 5 James D. Harper: A simple proof of 1 + 1 / 2 2 + 1 / 3 2 + … = π 2 / 6 {\displaystyle 1+1/2^{2}+1/3^{2}+\ldots =\pi ^{2}/6} The American Mathematical Monthly 109(6) (Jun. – Jul., 2003) 540–541.
Einzelnachweise ↑ Wolfgang Zeuge: Nützliche und schöne Geometrie . 3.3 Die Umkehrfunktionen. Springer Spektrum, Berlin 2021, ISBN 978-3-662-63831-6 , S. 46 . ↑ Eric W. Weisstein : Inverse Trigonometric Functions .MathWorld ↑ Derrick Henry Lehmer: Interesting Series Involving the Central Binomial Coefficient . Volume 92, 1985. Seite 452 ↑ James D.Harper, Another simple proof of 1 + 1 2 2 + 1 3 2 + ⋯ = π 2 6 {\displaystyle 1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}} , American Mathematical Monthly, Band 110, Nr. 6, 2003, S. 540–541 ↑ Georg Hoever: Höhere Mathematik kompakt . Springer Spektrum, Berlin Heidelberg 2014, ISBN 978-3-662-43994-4 (eingeschränkte Vorschau in der Google-Buchsuche).