Areafunktion
In der Mathematik bezeichnet man mit Areafunktionen die folgenden sechs Funktionen:
- Areasinus hyperbolicus und Areakosinus hyperbolicus
- Areatangens hyperbolicus und Areakotangens hyperbolicus
- Areasekans hyperbolicus und Areakosekans hyperbolicus
Sie sind die Umkehrfunktionen der Hyperbelfunktionen. Die Bezeichnung area (lat. Fläche) gibt an, dass diese den Flächeninhalt eines Sektors der Einheitshyperbel berechnen. Analog dazu berechnen die Arkusfunktionen (arcus lat. Bogen) die Bogenlänge eines Sektors des Einheitskreises
- Graphen der Areafunktionen
Literatur
- Yu. V. Sudorov: Inverse hyperbolic functions. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).
Auf dieser Seite verwendete Medien
Autor/Urheber: Geek3, Lizenz: CC BY 3.0
Plot of the area cosine hyperbolicus in the interval [1, 6]
Autor/Urheber: Geek3, Lizenz: CC BY 3.0
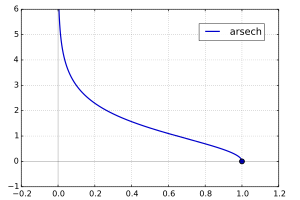
Plot of the inverse hyperbolic secant in the interval [0,1]
Autor/Urheber: Geek3, Lizenz: CC BY 3.0
Plot of the inverse hyperbolic cosecant in the interval [-5, 5]
Autor/Urheber: Geek3, Lizenz: CC BY 3.0
Plot of the inverse hyperbolic cotangent in the interval [-5.5, 5.5]
Autor/Urheber: Geek3, Lizenz: CC BY 3.0
Plot of the area sinus hyperbolicus in the interval [-5, 5]
Autor/Urheber: Geek3, Lizenz: CC BY 3.0
Plot of the area tangent hyperbolicus in the interval [-1, 1]