Affiner Raum

Der affine Raum (von lateinisch affinis ‚angrenzend, benachbart‘), gelegentlich auch lineare Mannigfaltigkeit genannt, nimmt im systematischen Aufbau der Geometrie eine Mittelstellung zwischen Euklidischem Raum und Projektivem Raum ein.

Der dreidimensionale affine Raum ist wie der euklidische Raum ein mathematisches Modell für den uns vertrauten dreidimensionalen Anschauungsraum. Dabei wird aber auf die Begriffe Länge, Abstand und Winkel verzichtet.

In einem weiteren Sinne kann ein affiner Raum, wie andere mathematische Räume auch, eine beliebige Dimension haben: Als affinen Raum kann man auch einen einzelnen Punkt, die affine Gerade, die affine Ebene sowie vier- und höherdimensionale Räume bezeichnen. In aller Regel sind diese Räume nur endlichdimensional.

Verschiedene mathematische Disziplinen haben unterschiedliche Präzisierungen dieses Begriffs gefunden.

Der affine Raum in der linearen Algebra

Definition

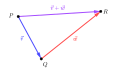
Gegeben seien eine Menge ${\displaystyle A\neq \emptyset }$, deren Elemente geometrisch als Punkte aufgefasst werden, ein Vektorraum ${\displaystyle V}$ über einem Körper ${\displaystyle K}$ und eine Abbildung von ${\displaystyle A\times A}$ nach ${\displaystyle V}$, die zwei Punkten ${\displaystyle P,Q\in A}$ einen Verbindungsvektor ${\displaystyle {\overrightarrow {PQ}}\in V}$ zuordnet, so dass die folgenden beiden Regeln gelten:

• für je drei Punkte ${\displaystyle P,Q,R\in A}$ gilt: ${\displaystyle {\overrightarrow {PQ}}+{\overrightarrow {QR}}={\overrightarrow {PR}}}$ (Dreiecksregel, Beziehung von Chasles),
• für jeden Punkt ${\displaystyle P\in A}$ und jeden Vektor ${\displaystyle {\vec {v}}\in V}$ gibt es einen eindeutig bestimmten Punkt ${\displaystyle Q\in A}$, so dass ${\displaystyle {\vec {v}}={\overrightarrow {PQ}}}$ (Abtragbarkeitsregel).^[1]

Das Tripel ${\displaystyle (A,V,{\overrightarrow {}})}$ heißt affiner Raum. Wenn klar ist, welcher Vektorraum ${\displaystyle V}$ und welche Pfeilabbildung ${\displaystyle {\overrightarrow {}}}$ zugrunde liegt, spricht man auch allein vom affinen Raum ${\displaystyle A}$. Bei dem Körper ${\displaystyle K}$ handelt es sich oft um den Körper ${\displaystyle \mathbb {R} }$ der reellen Zahlen.

Translationen

Im affinen Raum ist eine „Addition“ als Abbildung von ${\displaystyle A\times V\to A,\ (P,{\vec {v}})\mapsto P+{\vec {v}},}$ dadurch definiert, dass ${\displaystyle P+{\vec {v}}}$ gerade der über ${\displaystyle {\vec {v}}={\overrightarrow {PQ}}}$ eindeutig bestimmte Punkt ${\displaystyle Q}$ ist. Für festgelegtes ${\displaystyle {\vec {v}}\in V}$ heißt die zugehörige Abbildung ${\displaystyle T_{\vec {v}}\colon A\to A,\ P\mapsto P+{\vec {v}},}$ Translation (Verschiebung) oder präzise Translation um den Vektor ${\displaystyle {\vec {v}}}$ und ${\displaystyle {\vec {v}}}$ heißt dann der zugehörige Translationsvektor.

Translationen sind stets Bijektionen. Sie bilden zusammen mit der Hintereinanderschaltung als Gruppenverknüpfung eine Untergruppe der Automorphismengruppe ${\displaystyle \operatorname {Aut} (A)}$ von ${\displaystyle A}$, wobei ${\displaystyle {T_{\vec {0}}}=\operatorname {id} _{A}}$ und für ${\displaystyle {\vec {v}},{\vec {w}}\in V}$ stets ${\displaystyle {T_{\vec {v}}}\circ {T_{\vec {w}}}=T_{{\vec {v}}+{\vec {w}}}}$ und ${\displaystyle {T_{\vec {v}}}^{-1}=T_{-{\vec {v}}}}$ gelten^[2].

Anmerkung: Wegen ${\displaystyle P+{\overrightarrow {PQ}}=Q}$ schreibt man auch oft ${\displaystyle Q-P}$ statt ${\displaystyle {\overrightarrow {PQ}}}$. Es gilt dann ${\displaystyle {\vec {v}}=Q-P}$ genau dann, wenn ${\displaystyle Q=P+{\vec {v}}}$.

Affiner Unterraum

Wenn ${\displaystyle P}$ ein festgelegter Punkt aus ${\displaystyle A}$ ist und ${\displaystyle U}$ ein Untervektorraum von ${\displaystyle V}$, dann ist ${\displaystyle B=P+U=\{P+{\vec {u}}\mid {\vec {u}}\in U\}}$ ein affiner Unterraum von ${\displaystyle A}$. Anstelle des Begriffs „affiner Unterraum“ wird auch oft die äquivalente Bezeichnung affiner Teilraum verwendet. Der zu einem affinen Teilraum ${\displaystyle B}$ gehörige Untervektorraum ${\displaystyle U}$ ist durch ${\displaystyle B}$ eindeutig bestimmt.

Die Dimension eines affinen Raums ${\displaystyle A}$ zu einem Vektorraum ${\displaystyle V}$ über einem Körper ${\displaystyle K}$ ist definiert als die Dimension des Vektorraums ${\displaystyle V}$ über ${\displaystyle K}$. Oft ist es bequem, auch die leere Menge als affinen (Teil-)Raum anzusehen. Diesem leeren Teilraum wird dann die Dimension -1 zugeordnet.

Der affine Punktraum und der ihm zugeordnete Vektorraum

Wenn im affinen Raum ${\displaystyle A}$ ein Punkt ${\displaystyle O\in A}$ als Ursprung fest gewählt wird, hat man durch die Abbildung, die jedem Punkt ${\displaystyle P\in A}$ die Verschiebung ${\displaystyle {\overrightarrow {OP}}}$, den Ortsvektor von ${\displaystyle P}$, zuordnet, eine eineindeutige Abbildung zwischen dem affinen Raum und seinem Vektorraum der Verschiebungen. Dabei ist zu beachten, dass diese Zuordnung zwischen Punkten und Ortsvektoren von der Wahl des Ursprungs abhängt.

Umgekehrt kann man jeden Vektorraum ${\displaystyle V}$ als affinen Punktraum ansehen: ${\displaystyle V\times V\to V}$ mit ${\displaystyle ({\vec {v}},{\vec {w}})\mapsto {\vec {w}}-{\vec {v}}}$ ist die Abbildung, die zwei Punkten ihren Verbindungsvektor zuordnet. Damit wird von vornherein ein Punkt des affinen Raumes ausgezeichnet, nämlich der Nullvektor des Vektorraums.

Im ersten Fall kann nach der Identifizierung eines Punktes mit seinem Ortsvektor (abhängig von der Wahl des Ursprungs!), im zweiten Fall kann von vornherein die Addition im Vektorraum ${\displaystyle V}$ so aufgefasst werden, dass die Gruppe ${\displaystyle (V,+)}$ als Abbildungsgruppe der Verschiebungen auf sich selbst als Menge von Punkten operiert.

Aus diesen Gründen wird manchmal auf eine rigide Unterscheidung zwischen dem affinen Punktraum einerseits und dem Vektorraum der Verschiebungsvektoren andererseits verzichtet.

Beispiele

• Der ${\displaystyle n}$-dimensionale euklidische Raum ${\displaystyle E^{n}}$ ist der affine Raum über einem ${\displaystyle n}$-dimensionalen euklidischen Vektorraum (also einem ${\displaystyle n}$-dimensionalen Vektorraum mit Skalarprodukt).
• Jeder Vektorraum kann als affiner Raum aufgefasst werden. Dadurch ist auch jeder affine Unterraum eines Vektorraums ein affiner Raum.
• Die Lösungen eines inhomogenen linearen Gleichungssystems bilden einen affinen Raum über dem Vektorraum der Lösungen des zugehörigen homogenen Systems. Das gilt analog auch für Systeme linearer Differentialgleichungen.
• In der Differentialgeometrie spielen affine Räume eine Rolle in der Theorie der Faserbündel. Beispiele sind die Fasern des affinen Tangentialbündels, des Zusammenhangsbündels und von Jetbündeln.

Verwendung in der algebraischen Geometrie

• In der klassischen algebraischen Geometrie ist der ${\displaystyle n}$-dimensionale affine Raum ${\displaystyle A^{n}}$ über einem algebraisch abgeschlossenen Körper ${\displaystyle K}$ die algebraische Varietät ${\displaystyle K^{n}}$.
• In der modernen algebraischen Geometrie ist der ${\displaystyle n}$-dimensionale affine Raum ${\displaystyle A_{A}^{n}}$ über einem kommutativen Ring ${\displaystyle A}$ mit Einselement definiert als das Spektrum des Polynomringes ${\displaystyle A[X_{1},\dotsc ,X_{n}]}$ in ${\displaystyle n}$ Unbestimmten.
  Für eine ${\displaystyle A}$-Algebra ${\displaystyle B}$ sind die ${\displaystyle B}$-wertigen Punkte von ${\displaystyle A_{A}^{n}}$ gleich ${\displaystyle B^{n}}$.

Definitionen der synthetischen Geometrie

Ein affiner Raum im Sinne der synthetischen Geometrie besteht aus den folgenden Daten:

• einer Menge von Punkten,
• einer Menge von Geraden,
• einer Inzidenzrelation, die angibt, welche Punkte auf welchen Geraden liegen und
• einer Parallelitätsrelation, die angibt, welche Geraden parallel sind,

so dass gewisse Axiome erfüllt sind, die die Anschauung nahelegt (unter anderem Euklids berühmtes Parallelenaxiom).

Die so definierten Strukturen verallgemeinern den Begriff affiner Raum, der im vorliegenden Artikel definiert wird. So gilt:

1. Jeder zweidimensionale affine Raum erfüllt die Forderungen an eine affine Ebene. Eine affine Ebene, die den Satz von Desargues erfüllt, bestimmt einen eindeutigen Schiefkörper, so dass sie geometrisch isomorph zum zweidimensionalen affinen Raum über diesem Schiefkörper ist.
2. Jeder affine Raum erfüllt die Forderungen an eine affine Geometrie. Eine affine Geometrie, die mindestens dreidimensional ist (d. h., die eine affine Ebene als echten Teilraum enthält), erfüllt den Satz von Desargues und bestimmt einen eindeutigen Schiefkörper, so dass sie geometrisch isomorph zu einem mindestens dreidimensionalen Raum über diesem Schiefkörper ist.
3. Jeder affine Raum ist ein schwach affiner Raum.
4. Jeder endliche, mindestens zweidimensionale affine Raum ist ein Blockplan.

→ Siehe für weitere Details die genannten Artikel, in denen die verallgemeinerten Strukturen beschrieben sind. Wie sich der Begriff „affiner Raum“ (als Raum mit Verschiebungen, die einen Vektorraum bilden) von den axiomatischen Begriffen der synthetischen Geometrie abgrenzen lässt, wird im Artikel Affine Geometrie genauer dargestellt.

Siehe auch

• Affine Koordinaten

Weblinks

• Der affine Raum mit Beispielen von Joachim Mohr
• Hubert Grassmann: Vorlesungsskript Lineare Algebra. (PDF; 1,4 MB)

Literatur

• Gerd Fischer: Analytische Geometrie. 6., überarbeitete Auflage. Vieweg, Braunschweig/Wiesbaden 1992, ISBN 3-528-57235-3. 
• Siegfried Guber: Lineare Algebra und analytische Geometrie. 2., unveränderte Auflage. Universitätsbuchhandlung Rudolf Merkel, Erlangen 1970 (Vorlesung, ausgearbeitet von Gerd Heinlein und Gunter Ritter). 
• Günter Pickert: Analytische Geometrie. 6., durchgesehene Auflage. Akademische Verlagsgesellschaft Geest & Portig, Leipzig 1967. 
• Rolf Brandl: Vorlesungen über Analytische Geometrie. Verlag Rolf Brandl, Hof 1996. 

Einzelnachweise und Anmerkungen

1. ↑ Rolf Brandl: Vorlesungen über Analytische Geometrie. Verlag Rolf Brandl, Hof 1996, S. 10 ff. 
2. ↑ Rolf Brandl: Vorlesungen über Analytische Geometrie. Verlag Rolf Brandl, Hof 1996, S. 14.