Achtzehneck

regelmäßiges Achtzehneck

Ein Achtzehneck oder Oktodekagon ist eine geometrische Figur. Es gehört zur Gruppe der Vielecke (Polygone). Es ist definiert durch achtzehn Eckpunkte.

Regelmäßiges Achtzehneck

Ein Spezialfall des Achtzehnecks ist das regelmäßige Achtzehneck, dessen Seiten alle gleich lang sind und dessen Eckpunkte auf einem gemeinsamen Umkreis liegen.

Mathematische Zusammenhänge

Formel für Winkelberechnungen

Der von zwei durch benachbarten Ecken gehenden Umkreisradien eingeschlossene Winkel (Zentriwinkel) beträgt

${\displaystyle \alpha ={\frac {360^{\circ }}{18}}=20^{\circ }}$.

Der Winkel, den zwei benachbarte Seitenkanten im ebenen, regelmäßigen Achtzehneck miteinander einschließen, beträgt

${\displaystyle \beta ={\frac {(18-2)}{18}}\cdot 180^{\circ }={\frac {16}{18}}\cdot 180^{\circ }=160^{\circ }}$.

Formel für die Seitenlänge

${\displaystyle s=2\cdot r_{u}\cdot \sin {\frac {\alpha }{2}}}$

${\displaystyle s=2\cdot r_{u}\cdot \sin {10^{\circ }}}$

${\displaystyle s\approx r_{u}\cdot 0{,}1736481777}$

Diagonalen

(c) Telling the Author: User Antonsusi from the German Wikipedia, CC BY 3.0 de

Achtzehneck mit Diagonalen

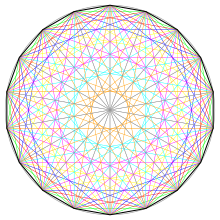
Im regelmäßigen Achtzehneck gibt es insgesamt 135 Diagonalen mit verschiedenen Längen:

• 18 Diagonalen über 2 (bzw. 16) Seiten
• 18 Diagonalen über 3 (bzw. 15) Seiten
• 18 Diagonalen über 4 (bzw. 14) Seiten
• 18 Diagonalen über 5 (bzw. 13) Seiten
• 18 Diagonalen über 6 (bzw. 12) Seiten
• 18 Diagonalen über 7 (bzw. 11) Seiten
• 18 Diagonalen über 8 (bzw. 10) Seiten
• 9 Diagonalen über 9 Seiten

Die Längen im Verhältnis zum Umkreisradius betragen:

• Die Diagonale über zwei Seiten entspricht der Seite eines Neunecks mit gleichem Umkreis:
  • ${\displaystyle s=2\cdot r_{u}\cdot \sin {20^{\circ }}\approx r_{u}\cdot 0{,}68404029}$
• Die Diagonale über drei Seiten entspricht der Seite eines Sechsecks mit gleichem Umkreis:
  • ${\displaystyle s=2\cdot r_{u}\cdot \sin {30^{\circ }}=r_{u}}$
• Die Diagonale über vier Seiten:
  • ${\displaystyle s=2\cdot r_{u}\cdot \sin {40^{\circ }}\approx r_{u}\cdot 1{,}28557522}$
• Die Diagonale über fünf Seiten:
  • ${\displaystyle s=2\cdot r_{u}\cdot \sin {50^{\circ }}\approx r_{u}\cdot 1{,}53208889}$
• Die Diagonale über sechs Seiten entspricht der Seite eines gleichseitigen Dreiecks mit gleichem Umkreis:
  • ${\displaystyle s=2\cdot r_{u}\cdot \sin {60^{\circ }}=r_{u}\cdot {\sqrt {3}}}$
• Die Diagonale über sieben Seiten:
  • ${\displaystyle s=2\cdot r_{u}\cdot \sin {70^{\circ }}\approx r_{u}\cdot 1{,}87938524}$
• Die Diagonale über acht Seiten:
  • ${\displaystyle s=2\cdot r_{u}\cdot \sin {80^{\circ }}\approx r_{u}\cdot 1{,}96961551}$
• Die Diagonale über neun Seiten entspricht dem Durchmesser des Umkreises:
  • ${\displaystyle s=2\cdot r_{u}}$

Formel für die Fläche

Konstruktion des Achtzehnecks, eine Abwandlung der Konstruktion des Neunecks mit Tomahawk.

Die Fläche A des regelmäßigen Achtzehnecks mit der Seitenlänge s beträgt

${\displaystyle A={\frac {18}{4}}\cdot s^{2}\cdot {\frac {\cos 10^{\circ }}{\sin 10^{\circ }}}}$

oder mit dem Umkreisradius

${\displaystyle A={\frac {18}{2}}\cdot r_{u}^{2}\cdot \sin 20^{\circ }}$.

Konstruktion

Das Achtzehneck wird durch Konstruktion eines Neunecks (zu Details siehe dortigen Artikel) und anschließende Winkel- oder Seitenhalbierung konstruiert. Weil ein regelmäßiges Neuneck nicht nur mit Zirkel und Lineal konstruiert werden kann, gilt das auch für das Achtzehneck. Man benötigt dazu zumindest ein Werkzeug zur Dreiteilung eines Winkels.

Regelmäßige überschlagene Achtzehnecke

Ein regelmäßiges überschlagenes Achtzehneck ergibt sich, wenn beim Verbinden der acht Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen ${\displaystyle \left\{n/k\right\}}$, wobei ${\displaystyle n}$ die Anzahl der Eckpunkte angibt und jeder ${\displaystyle k}$-te Punkt verbunden wird.

Es gibt nur zwei regelmäßige Achtzehnecksterne, auch Octodecagramme genannt.

Die „Sterne“ mit den Schläfli-Symbolen {18/2} und {18/16} sind Neunecke, die mit den Schläfli-Symbolen {18/3} und {18/15} sind Sechsecke sowie die mit den Schläfli-Symbolen {18/6} und {18/12} sind gleichseitige Dreiecke. Die Sterne mit den Schläfli-Symbolen {18/4} und {18/14} bzw. {18/8} und {18/10} sind regelmäßige Neunstrahlsterne auch Enneagramme genannt.

• Regelmäßige Achtzehnstrahlsterne
• 

  ${\displaystyle \left\{18/5\right\}{,}\ \left\{18/13\right\}}$

• 

  ${\displaystyle \left\{18/7\right\}{,}\ \left\{18/11\right\}}$

Verwendung des Achtzehnecks

(c) qwesy qwesy, CC BY 3.0

Befreiungshalle

Die um 1850 zum Andenken an Siege über Napoleon errichtete Befreiungshalle im bayrischen Kelheim hat einen achtzehneckigen Grundriss.