Analog-Digital-Umsetzer





Ein Analog-Digital-Umsetzer[1] ist ein elektronisches Gerät, Bauelement oder Teil eines Bauelements zur Umsetzung analoger Eingangssignale in einen digitalen Datenstrom, der dann weiterverarbeitet oder gespeichert werden kann. Weitere Namen und Abkürzungen sind ADU, Analog-Digital-Wandler oder A/D-Wandler, englisch ADC (analog-to-digital converter) oder kurz A/D.
Eine Vielzahl von Umsetz-Verfahren ist in Gebrauch. Das Gegenstück ist der Digital-Analog-Umsetzer (DAU).
Analog-Digital-Umsetzer sind elementare Bestandteile fast aller Geräte der modernen Kommunikations- und Unterhaltungselektronik wie z. B. Mobiltelefonen, Digitalkameras, oder Camcordern. Zudem werden sie zur Messwerterfassung in Forschungs- und industriellen Produktionsanlagen, in Maschinen und technischen Alltagsgegenständen wie Kraftfahrzeugen oder Haushaltsgeräten eingesetzt.
Arbeitsweise
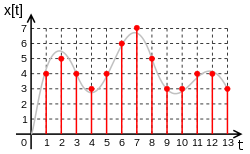
Ein ADU setzt ein zeit- und wert-kontinuierliches Eingangssignal (Analogsignal) in eine zeitdiskrete und wertdiskrete Folge von digital repräsentierten Werten um. Aufgrund einer endlichen Anzahl von möglichen Ausgangswerten erfolgt dabei immer eine Quantisierung. Das Ergebnis einer AD-Umsetzung kann man sich in einem Signal-Zeit-Diagramm in einer Punktfolge mit gestuften horizontalen und vertikalen Abständen vorstellen. Die Hauptparameter eines ADUs sind seine Bittiefe und seine maximale Abtastrate. Die Umsetzzeit ist meist wesentlich kleiner als das Reziproke der Abtastrate.
Schon die Bittiefe eines AD-Umsetzers begrenzt die maximal mögliche Genauigkeit, mit der das Eingangssignal umgesetzt werden kann. Die nutzbare Genauigkeit ist durch weitere Fehlerquellen des ADUs geringer. Neben möglichst schnellen Verfahren gibt es auch langsame (integrierende) Verfahren zur Unterdrückung von Störeinkopplungen.
Zeit-Diskretisierung (Abtastung)


Die minimal notwendige Abtastfrequenz für eine verlustfreie Diskretisierung ergibt sich aus der Bandbreite des Eingangssignals.
Um das Signal später vollständig rekonstruieren zu können, muss die Abtastfrequenz größer als das Doppelte der maximal möglichen Frequenz im Eingangssignal sein (siehe Nyquist-Frequenz). Anderenfalls kommt es zu einer Unterabtastung und führt im rekonstruierten Signal zu im Eingangssignal nicht vorhandenen Frequenzen. Daher muss das Eingangssignal bandbegrenzt sein. Entweder ist es dies von sich aus oder es wird durch Tiefpassfilterung zu solch einem Signal gemacht.
Manchmal ist das abzutastende Signal allerdings so hochfrequent, dass man diese Bedingung technisch nicht realisieren kann. Wenn das Eingangssignal jedoch periodisch ist, kann man durch Mehrfachabtastung mit zeitlichem Versatz dennoch eine Rekonstruktion ermöglichen, ohne dabei das Abtasttheorem zu verletzen, da bei mehrfachem Durchlauf des Signals Zwischenpunkte ermittelt werden und so eine größere Zahl von Stützstellen entsteht, was im Endeffekt einer Erhöhung der Abtastrate entspricht.
Während der Signalumsetzung darf sich bei vielen Umsetzverfahren das Eingangssignal nicht ändern. Dann schaltet man dem eigentlichen AD-Umsetzer eine Abtast-Halte-Schaltung (Sample-and-Hold-Schaltung) vor, die den Signalwert (englisch sample) analog so zwischenspeichert, dass er während der Quantisierung konstant bleibt. Dies trifft besonders auf die stufen- und bitweisen Umsetzer zu, die längere Umsetzzeiten benötigen. Wenn ein Umsetzer diese Abtast-Halte-Schaltung erfordert, so ist sie bei Realisierung als integrierter Schaltkreis heute meist enthalten.
In vielen Anwendungen soll das Eingangssignal in immer exakt gleichen Zeitabständen abgetastet werden. Durch zufällige Variationen der Abstände tritt jedoch ein Effekt auf, den man als Jitter bezeichnet. Er verfälscht das ursprüngliche Signal bei der späteren Rekonstruktion, da diese wieder äquidistant – also mit gleichen Zeitabständen – erfolgt.
Nicht verwechselt werden darf die Umsetzdauer mit der Latenzzeit eines Umsetzers, d. h. die Zeit, die nach der Erfassung vergeht, bis ein AD-Umsetzer das Datum weitergegeben hat. Diese Zeit kann weitaus größer als die Umsetzdauer sein, was insbesondere in der Regelungstechnik störend sein kann. Sie wird verursacht durch Pipelining des Umsetzers, Nachbearbeitung der Daten und die serielle Datenübertragung.
Quantisierung
Die Quantisierung des vorher zeitdiskretisierten Signals stellt den eigentlichen Übergang von einem analogen Signal zu einem digitalen Signal dar. Auf Grund der endlichen Bittiefe des Umsetzers gibt es nur eine gewisse Anzahl an Codeworten und deren dazugehörige Eingangsspannung. Das Signal wird quantisiert. Die Abweichung zwischen der wahren Eingangsspannung und der quantisierten Eingangsspannung nennt man Quantisierungsabweichung. Je mehr Bits bzw. Codeworte zur Verfügung stehen, umso kleiner ist diese unvermeidbare Abweichung. Bei einem idealen AD-Umsetzer verringert jedes zusätzliche Bit dieses Rauschen um 6,02 dB. Bei realen AD-Umsetzern kann man über die Effektive Anzahl von Bits (ENOB) abschätzen, was ein weiteres Bit bei dem betrachteten Umsetzer bringen würde (so würde ein weiteres Bit bei einem 12-bit-Umsetzer mit einem ENOB von 11 bit ca. 0,15 bit bzw. 0,9 dB bringen).
Das Verhältnis aus maximal möglicher unverzerrter Eingangsspannung und dem Rauschen bei signallosem Eingang nennt man Dynamikumfang. Umsetzer, die bei fehlendem Eingangssignal ein konstantes Codewort liefern, haben einen unendlich hohen Dynamikumfang. Sinnvoller ist die Angabe des Signal-Rausch-Verhältnisses (bzw. des SINAD, signal to noise and distortion ratio, Verhältnis des Signals zur Summe aus Rauschen und Verzerrungen).
Bezugswert
Da das dem ADU zugeführte Analogsignal in einen größenlosen Digitalwert umgesetzt wird, muss es mit einem vorgegebenen Wert oder Signal bewertet werden (Eingangssignalbereich bzw. Messbereich). Im Allgemeinen wird ein feststehender Bezugswert (z. B. eine intern erzeugte Referenzspannung) verwendet. Das analoge Eingangssignal wird digital abgebildet, die Referenz legt den zulässigen Scheitelwert des Eingangssignals fest.
Quantisierungskennlinie
Bei Analog-Digital-Umsetzern besteht zwischen Eingangs- und Ausgangsgröße immer ein nichtlinearer Zusammenhang. Ändert sich allerdings bei steigender Eingangsspannung der Digitalwert in konstanten Abständen oder nähert sich bei extrem feiner Stufung die Kennlinie einer Geraden, spricht man dennoch von einem linearen Analog-Digital-Umsetzer. Es gibt
| unipolare Ausführungen, beispielsweise im Dualsystem | ||
| 000…000 für 0 | 100…000 für /2 | 111…111 für – 1 LSB |
| bipolare Ausführungen, beispielsweise im Dualsystem mit Offset | ||
| 000…000 für /2 | 100…000 für 0 | 111…111 für /2 – 1 LSB |
wobei daneben auch andere Kodierungen, beispielsweise Zweierkomplement, BCD-Code verwendbar sind.
Interfaces
Neben der schon erwähnten Abtast-Halte-Schaltung werden weitere Schaltungen für das Interface in die analoge Welt benötigt, so dass diese vielfach zusammen mit dem eigentlichen Umsetzer auf einem Chip integriert sind. Dies können beispielsweise Puffer- bzw. Verstärkerschaltungen, ggf. mit umschaltbarer Verstärkung (Programmable Gain Amplifier (PGA)) sowie Eingänge für differenzielle Signalübertragung sein. Es gibt auch Varianten ohne echten Subtrahierverstärker am Eingang; stattdessen werden die beiden Leitungen des differentiellen Signals hintereinander verarbeitet und erst anschließend die Differenz gebildet (sog. pseudodifferentielle Eingänge)[2].
Am Ausgang werden digitale Daten zur Verfügung gestellt. Klassischerweise erscheint jedes Bit der Ausgangsgröße an einem eigenen Anschlusspin; die Größe wird also parallel ausgegeben – nicht zu verwechseln mit der Parallelumsetzung. Falls die Größe auf einer Anzeige angezeigt werden soll, kommen auch integrierte Siebensegment-Codierer zum Einsatz, oder die Größe wird als BCD-Code im Multiplexverfahren ausgegeben. Nachteilig an der parallelen Ausgabe, insbesondere bei der Weiterverarbeitung durch Mikroprozessoren oder -controllern, ist hierbei die große Anzahl an benötigten Anschlusspins. Daher werden vielfach serielle Verbindungen implementiert, beispielsweise mit den Protokollen I²C, SPI oder I²S. Bei entsprechenden Datenraten wird beispielsweise LVDS- oder JESD204B-Technik eingesetzt.
Abweichungen
Zusätzlich zu dem unvermeidbaren Quantisierungsfehler haben reale AD-Umsetzer folgende Fehler:
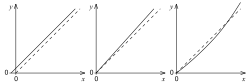
Nullpunktfehler, Verstärkungsfehler und Nichtlinearitätsfehler

a) additiv, b) multiplikativ, c) nicht linear
Als Abweichungen der Kennlinien zwischen realem und idealem Umsetzer sind folgende Fehler definiert (siehe Bild):
- Nullpunktfehler (Offset)
- Verstärkungsfehler (englisch gain error)
- Nichtlinearitätsfehler
Der Verstärkungsfehler wird oft als Bruchteil des aktuellen Wertes angegeben, der Nullpunktfehler zusammen mit dem Quantisierungsfehler und der Nichtlinearitätsfehler als Bruchteile des Endwertes oder als Vielfache eines LSB.
Fehler in der Stufung

a) bei ungleicher Breite einer Stufe,
b) bei fehlerhafter Breite einer höherwertigen Stufe
Einzelne Stufen können unterschiedlich breit ausfallen.
Bei kontinuierlich steigender Eingangsgröße kann es je nach Realisierungsverfahren vorkommen, dass ein Wert der Ausgangsgröße übersprungen wird, insbesondere dann, wenn es einen Übertrag über mehrere Binärstellen gibt, beispielsweise von 0111 1111 nach 1000 0000. Man spricht hierzu von „missing codes“.
Zeitliche und Apertur-Fehler
Bei Wandlung jedes nichtkonstanten Eingangssignals entsteht durch zeitliche Schwankungen des Umsetzer-Taktes Δt (clock jitter) ein der zeitlichen Änderung des Eingangssignals proportionaler Fehler. Bei einem Sinussignal der Frequenz f und der Amplitude A beträgt es . Jeglicher Jitter erzeugt weiteres Rauschen – es gibt keinen Schwellwert, unterhalb dem es zu keiner Verschlechterung des Signal-Rausch-Verhältnisses kommt. Viele aktuelle Wandler (insbesondere Delta-Sigma-Umsetzer) haben eine interne Taktaufbereitung. Der Hintergrund ist der, dass viele Wandler einen höheren internen Takt benötigen bzw. bei Delta-Sigma-Umsetzern, dass dort Jitter direkt (d. h. auch bei konstantem Eingangssignal) Wandlungsfehler verursacht.
Realisierungsverfahren
Es gibt eine große Anzahl von Verfahren, die zur Umsetzung von analogen in digitale Signale benutzt werden können. Im Folgenden sind die wichtigsten Prinzipien aufgeführt. Als Eingangsgröße wird in allen Beispielen die elektrische Spannung zugrunde gelegt.
Den inneren Ablauf einer Umsetzung steuern die Bausteine selbst. Für die Zusammenarbeit mit einem Rechner kann ein ADU mit einem Start-Eingang versehen sein für die Anforderung zu einer neuen Umsetzung, mit einem „busy“-Ausgang für die Meldung der noch andauernden Umsetzung und mit bus-kompatiblen Datenausgängen für das Auslesen des entstandenen Digitalwertes.
Integrierender Umsetzer (Zählverfahren)
Bei diesen Verfahren finden zwei Vorgänge statt:
- ein analoger durch die Messgröße beeinflusster Prozess, bei dem ein Kondensator stetig geladen wird und im Wechsel wieder entladen,
- ein digitaler Prozess, der vom Ladevorgang abhängige Zeiten oder Impulsdichten misst, wozu gezählt wird.
Beim Nachlauf-Umsetzer wird ebenfalls gezählt. Dieser wird ohne Kondensator als rückgekoppelter Umsetzer betrieben und weiter unten erklärt.
Single-Slope-Umsetzer (Sägezahn-/Einrampenverfahren)

Beim Sägezahnverfahren wird die Ausgangsspannung eines Sägezahngenerators über zwei Komparatoren K1 und K2 mit dem Massepotenzial (0 V) und mit der ADU-Eingangsspannung verglichen. Während des Zeitraums, in dem die Sägezahnspannung den Bereich zwischen 0 V und der Spannung durchläuft, werden die Impulse eines Quarzoszillators gezählt. Aufgrund der konstanten Steigung der Sägezahnspannung ist die verstrichene Zeit und somit der Zählerstand bei Erreichen von proportional zur Höhe der ADU-Eingangsspannung. Zum Ende des Zählvorgangs wird das Zählergebnis in ein Register übertragen und steht als digitales Signal zur Verfügung. Anschließend wird der Zähler zurückgesetzt, und ein neuer Umsetzungsvorgang beginnt.
Die Umsetzungszeit bei diesem ADU ist abhängig von der Eingangsspannung. Schnell veränderliche Signale können mit diesem Umsetzertyp nicht erfasst werden. Umsetzer nach dem Sägezahnverfahren sind ungenau, da der Sägezahngenerator mit Hilfe eines temperatur- und alterungsabhängigen Integrationskondensators arbeitet. Sie werden wegen ihres relativ geringen Schaltungsaufwands für einfache Aufgaben eingesetzt, beispielsweise in Spielkonsolen, um die Stellung eines Potentiometers, das durch einen Joystick oder ein Lenkrad bewegt wird, zu digitalisieren.
Dual- und Quadslope-Umsetzer (Mehrrampenverfahren)
Dual- und Quadslope-Umsetzer bestehen im Wesentlichen aus einem Integrator und mehreren Zählern und elektronischen Schaltern. Der Integrator arbeitet mit einem externen, hochwertigen Kondensator, der in zwei oder mehr Zyklen geladen und entladen wird. Beim Zweirampenverfahren (Dual-Slope) wird zunächst der Integratoreingang mit der unbekannten ADU-Eingangsspannung verbunden, und es erfolgt die Ladung über ein fest vorgegebenes Zeitintervall. Für die anschließende Entladung wird der Integrator mit einer bekannten Referenzspannung entgegengesetzter Polarität verbunden. Einzelheiten werden unter digitale Messtechnik erläutert. Die benötigte Entladezeit bis zum Erreichen der Spannung null am Integratorausgang wird durch einen Zähler ermittelt; der Zählerstand steht bei geeigneter Dimensionierung unmittelbar für die Eingangsspannung. Die Größe der Kapazität kürzt sich bei diesem Verfahren aus dem Ergebnis heraus. Zur Korrektur des Nullpunktfehlers des ADU wird beim Vierrampenverfahren noch ein weiterer Lade-/Entladezyklus bei kurzgeschlossenem Integratoreingang durchgeführt. Die Referenzspannung ist die bestimmende Größe für die Genauigkeit; das heißt beispielsweise, dass thermisch bedingte Schwankungen vermieden werden müssen.
Derartige Umsetzer nach dem Mehrrampenverfahren sind langsam, benötigen keine Abtast-Halte-Schaltung und bieten eine hohe Auflösung sowie gute differentielle Linearität und gute Unterdrückung von Störsignalen wie Rauschen oder Netzeinkopplung. Das typische Einsatzgebiet sind anzeigende Messgeräte (Digitalmultimeter), die kaum eine Umsetzzeit unter 500 ms benötigen und bei geeigneter Integrationsdauer überlagerte 50-Hz-Störungen der Netzfrequenz eliminieren können.
Ladungsbilanz-Umsetzer
Beim Ladungsbilanzverfahren (Charge-Balancing-Verfahren) wird der Kondensator eines Integrators durch einen zur Eingangsgröße proportionalen elektrischen Strom geladen und durch kurze Stromstöße in entgegengesetzter Richtung entladen, so dass sich im Mittel keine Ladung aufbaut. Je größer der Ladestrom ist, desto häufiger wird entladen. Die Häufigkeit ist proportional zur Eingangsgröße; die Anzahl der Entladungen in einer festen Zeit wird gezählt und liefert den Digitalwert. In seinem Verhalten ist das Verfahren dem Dual-Slope-Verfahren ähnlich. Auch andere analoge Eingangsstufen, die einen Spannungs-Frequenz-Umformer mit genügend hochwertiger Genauigkeit enthalten, führen über eine Frequenzzählung auf einen Digitalwert.
Rückgekoppelter Umsetzer (Serielles Verfahren)

Diese arbeiten mit einem DAU, der einen Vergleichswert liefert. Dieser wird nach einer geeigneten Strategie an das analoge Eingangssignal angenähert. Der zum Schluss am DAU eingestellte Digitalwert ist das Ergebnis des ADU. Da das Verfahren eine Zeitspanne benötigt, in der sich das Eingangssignal nicht ändern darf, wird davon mittels Sample-and-Hold-Schaltung (S/H) eine „Probe“ genommen und während der Umsetzung festgehalten.
Nachlauf-Umsetzer
Hier wird ein Zähler als Datenspeicher eingesetzt. Je nach Vorzeichen von wird um einen Schritt aufwärts oder abwärts gezählt und neu verglichen – gezählt und neu verglichen, bis die Differenz kleiner ist als der kleinste einstellbare Schritt. Diese Umsetzer „fahren“ dem Signal einfach nach, wobei die Umsetzungszeit vom Abstand des aktuellen Eingangssignals zum Signal bei der letzten Umsetzung abhängt.
Sukzessive Approximation
Diese arbeiten mit einem DAU, der einen Vergleichswert jedes Mal neu aufbaut. Das Eingangssignal wird mittels Intervallschachtelung eingegrenzt. Einfache sukzessive Approximation setzt dabei pro Schritt ein Bit um. Ein um Größenordnungen genaueres und schnelleres Umsetzen kann dadurch erreicht werden, dass die Umsetzung redundant erfolgt, indem mit kleinerer Schrittweite umgesetzt wird, als einem Bit entspricht.
Wägeverfahren

Ein mögliches Approximationsverfahren ist das Wägeverfahren. Dabei werden in einem Datenspeicher (successive approximation register, SAR) zunächst alle Bits auf null gesetzt. Beginnend beim höchstwertigen Bit (Most Significant Bit, MSB) werden abwärts bis zum niederwertigsten Bit (Least Significant Bit, LSB) nacheinander alle Bits des Digitalwerts ermittelt.
Vom Steuerwerk wird jeweils das in Arbeit befindliche Bit probeweise auf eins gesetzt; der Digital-Analog-Umsetzer erzeugt die dem aktuellen Digitalwert entsprechende Vergleichsspannung. Der Komparator vergleicht diese mit der Eingangsspannung und veranlasst das Steuerwerk, das in Arbeit befindliche Bit wieder auf null zurückzusetzen, wenn die Vergleichsspannung höher ist als die Eingangsspannung. Sonst ist das Bit mindestens notwendig und bleibt gesetzt. Nach der Einstellung des niederwertigsten Bits ist kleiner als der kleinste einstellbare Schritt.
Während der Umsetzung darf sich das Eingangssignal nicht ändern, da sonst die niederwertigen Bits auf Grundlage der festgestellten, aber nicht mehr gültigen höherwertigen Bits gewonnen würden. Deshalb ist dem Eingang eine Abtast-Halte-Schaltung (S/H) vorgeschaltet. Für jedes Bit an Genauigkeit benötigt der ADU jeweils einen Taktzyklus Umsetzungszeit. Derartige Umsetzer erreichen Auflösungen von 16 Bit bei einer Umsetzungsrate von 1 MHz.
Redundante Umsetzer
Dem Wägeverfahren ähnliche redundante Analog-Digital-Umsetzer gehen davon aus, dass keine exakte Halbierung des noch offenen Intervalls um den Zielwert herum erfolgt, sondern dieses Intervall nur um einen Anteil davon eingeschränkt wird. Dazu haben sie einen Digital-Analog-Umsetzer, dessen Elemente nicht nach dem Dualsystem gestaffelt sind, also immer um den Faktor 2, sondern um einen kleineren Faktor. Sie nehmen damit einerseits in Kauf, dass mehr Elemente benötigt werden, um den gleichen Wertebereich abzudecken, ermöglichen aber andererseits, dass der Umsetzer um eine Größenordnung schneller arbeiten und eine um mehrere Größenordnungen höhere Genauigkeit erzielen kann: Die schnellere Funktion kommt dadurch, dass der Komparator in jedem Schritt nicht abwarten muss, bis sich seine Verstärker bis zu einem Mehrfachen der Zielgenauigkeit eingeschwungen haben (immer etwas größenordnungsmäßig so viele Einschwing-Zeitkonstanten, wie der Umsetzer Bits umsetzen soll), sondern eine Entscheidung schon nach der kurzen 50-Prozent-Einschwingzeit abgeben kann, die dann in einem recht großen Bereich innerhalb des Restintervalls fehlerhaft ist. Das wird allerdings mehr als abgefangen durch die redundant ausgelegten Umsetzerelemente. Die Gesamtumsetzdauer eines solchen Umsetzers liegt größenordnungsmäßig eine Zehnerpotenz unter der seines einfachen Vorbilds. Durch den redundanten Umsetzungsprozess hat ein solcher Umsetzer ein viel geringeres Eigenrauschen als sein rein dualer Gegenpart.
Zusätzlich kann sich ein solcher ADU selbst einmessen, und zwar bis zu einer Genauigkeit, die nur durch das Rauschen begrenzt ist. Indem man das Selbsteinmessen wesentlich langsamer ablaufen lässt als die Umsetzung in der Nutzanwendung, kann der Rauscheinfluss in diesem Prozess um eine Größenordnung gedrückt werden. Die resultierende Kennlinie eines solchen Umsetzers ist bis auf eine rauschartige Abweichung um wenige Vielfache des kleinsten beim Selbsteinmessen verwendeten Elements absolut linear. Indem zwei derartige Umsetzer nebeneinander auf denselben Chip platziert werden und einer immer im Einmess-Modus ist, können solche Umsetzer nahezu resistent gegen Herstellungstoleranzen, Temperatur- und Betriebsspannungsänderungen gemacht werden. Die erreichbare Auflösung ist ausschließlich rauschbegrenzt.
Delta-Sigma-Verfahren

Das Delta-Sigma-Verfahren, auch als 1-Bit-Umsetzer bezeichnet, basiert auf der Delta-Sigma-Modulation. In der einfachsten Form (Modulator erster Ordnung) kommt das Eingangssignal über einen analogen Subtrahierer zum Integrator und verursacht an dessen Ausgang ein Signal, das von einem Komparator mit eins oder null bewertet wird. Ein Flipflop erzeugt daraus ein zeitdiskretes binäres Signal, mit dem ein 1-Bit-Digital-Analog-Umsetzer in eine positive oder negative elektrische Spannung liefert, die über den Subtrahierer den Integrator wieder auf null zurückzieht (Regelkreis). Ein nachgeschalteter Digitalfilter setzt den seriellen und hochfrequenten Bit-Strom in Daten niedriger Erneuerungsrate, aber großer Bitbreite (16 oder 24 Bit) und hohem Signal-Rausch-Verhältnis (94 bis 115 dB) um. In der Praxis werden Delta-Sigma-Umsetzer als Systeme dritter oder vierter Ordnung aufgebaut, das heißt durch mehrere seriell angeordnete Differenz- und Integratorstufen. Dies erlaubt eine bessere Rauschformung und damit einen höheren Gewinn an Auflösung bei gleicher Überabtastung.
Ein Vorteil des Delta-Sigma-Umsetzers ist, dass die Dynamik in gewissen Grenzen durch die Bandbreite wechselseitig ausgetauscht werden kann. Durch die kontinuierliche Abtastung am Eingang wird auch keine Halteschaltung (engl. sample and hold) benötigt. Außerdem werden geringe Anforderungen an das analoge Anti-Aliasing-Filter gestellt.
Die Vorteile werden durch den Nachteil der vergleichsweise hohen Latenzzeit erkauft, welche vor allem durch die digitalen Filterstufen bedingt ist. Delta-Sigma-Umsetzer werden daher dort eingesetzt, wo kontinuierliche Signalverläufe und nur moderate Bandbreiten benötigt werden, wie beispielsweise im Audiobereich. Praktisch alle Audiogeräte im Bereich der Unterhaltungselektronik wie zum Beispiel DAT-Rekorder setzen diese Umsetzer ein.
Auch bei Datenumsetzern in der Kommunikationstechnik und der Messtechnik wird es aufgrund der fallenden Preise zunehmend eingesetzt. Durch die dabei notwendige hohe Überabtastung sind dem Verfahren bei höheren Frequenzen allerdings Grenzen gesetzt.
Parallel-Umsetzer

Einstufige Parallelumsetzer (Flash-Umsetzer)
Während die sukzessive Approximation mehrere Vergleiche mit nur einem Komparator ausführt, kommt die direkte Methode oder auch Flash-Umsetzung mit nur einem Vergleich aus. Dazu ist bei Flash-Umsetzern aber für jeden möglichen Ausgangswert (bis auf den größten) ein separat implementierter Komparator erforderlich. Beispielsweise ein 8-Bit-Flash-Umsetzer benötigt somit 28−1 = 255 Komparatoren.
Das analoge Eingangssignal wird im Flash-Umsetzer gleichzeitig von allen Komparatoren mit den (über einen linearen Spannungsteiler erzeugten) Vergleichsgrößen verglichen. Anschließend erfolgt durch eine Kodeumsetzung der 2n−1 Komparatorsignale in einen n bit breiten Binärkode (mit n: Auflösung in Bit). Das Resultat steht damit nach den Durchlaufverzögerungen (Schaltzeit der Komparatoren sowie Verzögerung in der Dekodierlogik) sofort zur Verfügung. Im Ergebnis sind die Flash-Umsetzer also sehr schnell, bringen aber im Allgemeinen auch hohe Verlustleistungen und Anschaffungskosten mit sich (insbesondere bei den hohen Auflösungen).

H steht für HIGH = positiv übersteuert, L für LOW = negativ übersteuert.
Die Codeumsetzung erfordert unabhängig von der Auflösung nur eine Spalte mit Und-Gattern und eine Spalte mit Oder-Gattern (siehe Bild). Sie rechnet das Ergebnis der Komparatoren um in eine Binärzahl. Sie arbeitet mit einer sehr kurzen und für alle Binärziffern gleich langen Durchlaufverzögerung. Für die vier möglichen Werte eines Zwei-Bit-Umsetzers sind drei Komparatoren erforderlich. Der vierte hat nur die Funktion, eine Messbereichsüberschreitung zu signalisieren und die Codeumsetzung zu unterstützen.
Mehrstufige Parallelumsetzer (Pipeline-Umsetzer)

Pipeline-Umsetzer sind mehrstufige Analog-Digital-Umsetzer mit mehreren selbständigen Stufen, die in Pipeline-Architektur aufgebaut sind. Ihre Stufen bestehen in der Regel aus Flash-Umsetzern über wenige Bits.
In jeder Pipelinestufe wird eine grobe Quantisierung vorgenommen, dieser Wert wieder mit einem DAU in ein analoges Signal umgesetzt und vom zwischengespeicherten Eingangssignal abgezogen. Der Restwert wird verstärkt der nächsten Stufe zugeführt. Der Vorteil liegt in der stark verminderten Anzahl an Komparatoren, z. B. 30 für einen zweistufigen Acht-Bit-Umsetzer. Ferner kann eine höhere Auflösung erreicht werden. Die Mehrstufigkeit erhöht die Latenzzeit, aber vermindert die Abtastrate nicht wesentlich. Die Pipeline-Umsetzer haben die echten Parallelumsetzer außer bei extrem zeitkritischen Anwendungen ersetzt. Diese mehrstufigen Umsetzer erreichen Datenraten von 250 MSPS (Mega-Samples Per Second) bei einer Auflösung von 12 Bit (MAX1215, AD9480) oder eine Auflösung von 16 Bit bei 200 MSPS (ADS5485).
Die Werte der Quantisierungsstufen werden unter Berücksichtigung ihrer Gewichtung addiert. Meistens enthält ein Korrektur-ROM noch Kalibrierungsdaten, die dazu dienen, Fehler zu korrigieren, die in den einzelnen Digitalisierungsstufen entstehen. Bei manchen Ausführungen werden diese Korrekturdaten auch auf ein externes Signal hin generiert und in einem RAM abgelegt.
Pipeline-Umsetzer kommen normalerweise in allen Digitaloszilloskopen und bei der Digitalisierung von Videosignalen zur Anwendung. Als Beispiel ermöglicht der MAX109 bei einer Auflösung von 8 bit eine Abtastrate von 2,2 GHz.[3] Mittlerweile gibt es aber noch schnellere (4 GSPS) und genauere Umsetzer (16 bit @1 GSPS). Bei heutigen Digitaloszilloskopen mit möglichen Abtastraten von 240 GSPS werden zusätzlich noch Demultiplexer vorgeschaltet.
Hybrid-Umsetzer
Ein Hybrid-Umsetzer ist kein eigenständiger Umsetzer, sondern er kombiniert zwei oder mehr Umsetzungsverfahren, zum Beispiel auf Basis einer SAR-Struktur, wobei der ursprüngliche Komparator durch einen Flash-Umsetzer ersetzt wird. Dadurch können in jedem Approximationsschritt mehrere Bits gleichzeitig ermittelt werden.
Marktsituation
Am Markt kommen im Wesentlichen vier Verfahren vor:
- Für hohe Abtastraten kommen Pipeline-Umsetzer zum Einsatz. Geschwindigkeiten 40 MSPS bis 5 GSPS. Übliche Dynamik 8 Bit, 12 Bit (bis 4 GSPS) oder 16 Bit (bis 1 GSPS).
- Kommt es auf hohe Genauigkeit bei gemäßigter Abtastraten an und spielt Latenz keine Rolle, kommen Delta-Sigma-Umsetzer zum Einsatz. Geschwindigkeiten wenige SPS bis 2,5 MSPS. Bittiefen 16 Bit bis 24 Bit.
- Ist die Latenz wesentlich oder stört das vergleichsweise steile Tiefpassverhalten, kommen sukzessiv approximierende Umsetzer zum Einsatz. Geschwindigkeiten 0,1 MSPS bis 10 MSPS.
- In einfachen anzeigenden Messgeräten wie Multimeter kommen langsame Störungen dämpfende Zählverfahren wie Dualslope-Umsetzer zum Einsatz.
Mit diesen Verfahren kann man fast alle praktischen Anforderungen abdecken und bei gemäßigten Anforderungen (z. B. 12 bit, 125 KSPS, 4 Kanäle) sind diese Wandler kostengünstig (ca. 1 €) zu bekommen.
Wichtige Kenngrößen
- Abtastrate (Sample Rate) – Angabe zur Häufigkeit der Umsetzung.
- Auflösung (Resolution) – Breite der Stufen (auch Anzahl der Stufen oder Anzahl der Stellen), die zur Darstellung des Ausgangssignals verwendet werden.
- Nullpunktsfehler – Die Umsetzerkennlinie (ohne Berücksichtigung der Stufung) ist verschoben. Der digitale Wert unterscheidet sich vom richtigen Wert um einen konstanten Betrag.
- Empfindlichkeitsfehler, Verstärkungsfehler – Die Umsetzerkennlinie (ohne Berücksichtigung der Stufung) ist verdreht (Steigungsfehler). Der digitale Wert unterscheidet sich vom richtigen Wert um einen konstanten Prozentsatz der Eingangsgröße.
- Integrale Nichtlinearität – Der Fehler dadurch, dass eine als linear zugrunde gelegte Umsetzerkennlinie (ohne Berücksichtigung der Stufung) nicht geradlinig ist.
- Differenzielle Nichtlinearität – Abweichung der Breite der Umsetzungsstufen untereinander
- Quantisierungskennlinie – Grafische Darstellung des Zusammenhangs zwischen den digitalen Ausgangswerten und den analogen Eingangswerten, z. B. einem linearen oder logarithmischen Verlauf folgend.
- Quantisierungsfehler – Durch die begrenzte Auflösung bedingte Abweichung des Ausgangssignals vom funktionalen (stetigen) Verlauf.
- Informationslücke (Missing Code) – Wenn eine kontinuierliche Vergrößerung des Eingangssignals keine fortlaufend durchnummerierten Werte des Ausgangscodes zur Folge hat, sondern ein Wert übersprungen wird; möglich bei einer differenziellen Nichtlinearität von mehr als 1 LSB.
- Latenzzeit – Laufzeitverzögerung von der Erfassung des Eingangssignals bis zur Bereitstellung des zugehörigen Ausgangssignals.
- Signal-Rausch-Verhältnis in dB
- Dynamikumfang in dB
- Dynamische Parameter
- Intermodulationsstörungen in dB
- Betriebsstrom – je schneller die Umsetz-Elektronik arbeiten muss, desto höherer wird ihr Versorgungsstrom (Eigenerwärmung).
Siehe auch
- Antialiasing (Signalverarbeitung)
- Dithering (Audiotechnik)
- Digitale Messtechnik
- Vielkanalanalysator
- Liste von Audio-Fachbegriffen
Literatur
- Rudy J. van de Plassche: CMOS integrated analog-to-digital and digital-to-analog converters. 2. Auflage. Kluwer Academic, Boston 2003, ISBN 1-4020-7500-6 (englisch).
- Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 12. Auflage. Springer, Heidelberg 2002, ISBN 3-540-42849-6.
- Rüdiger Klein: Das neue Werkbuch Elektronik. Bercker, Kevelaer, ISBN 978-3-645-65094-6.
Weblinks
- Literatur über Analog-Digital-Umsetzer im Katalog der Deutschen Nationalbibliothek
- Eine Einführung in Delta-Sigma-Wandler
- AD-Umsetzer in „Angewandte Mikroelektronik“ – Grundlagen
- Pipelined Subranging ADCs (PDF; 1 MB)
Einzelnachweise
- ↑ Von den gebräuchlichen Begriffen wird hier derjenige verwendet, der für die Ingenieurwissenschaften durch Normung in DIN 1319-2 festgelegt worden ist.
- ↑ Application Note 1108 – Understanding Single-Ended, Pseudo-Differential and Fully-Differential ADC Inputs. Maxim Integrated, 14. Juni 2002, archiviert vom am 29. August 2014; abgerufen am 12. Dezember 2018 (englisch).
- ↑ Datenblatt des Flash-Umsetzers MAX109 (PDF; 452 KiB).
Auf dieser Seite verwendete Medien
Autor/Urheber: Saure 10:20, 13. Apr. 2010 (CEST), Lizenz: CC BY-SA 3.0 de
Kennlinie eines Parallelumsetzers
*Red: Discrete and quantizied (digital) signal without the zero-order sample&hold.
- Grey: source, analog signal
Autor/Urheber: Chepry 💬 (Andrzej Barabasz) 📷 🇵🇱, Lizenz: CC BY-SA 3.0
Wolfson Microelectronics WM8775SEDS
a high performance 4-channel stereo multiplexed ADC
102 dB SNR A weighted at 48 kHz, -90 dB THD and ADC sampling frequency between 32kHz and 96kHz
placed on Sound Blaster X-Fi sound card
Autor/Urheber: Mister rf, Lizenz: CC BY-SA 4.0
8-Bit Successive Approximation Analog-to-Digital Converter
Werte in verschiedenen Stufen des Delta-Sigma-Umsetzers bei sinusförmigem Eingangssignal
Autor/Urheber: Saure, Lizenz: CC BY-SA 3.0
Nullpunktsabweichung, Empfindlichkeitsabweichung, Linearitätsabweichung
Autor/Urheber: Mister rf, Lizenz: CC BY-SA 4.0
Analog Devices designed the first monolithic ADC, the 10-bit AD571, in 1978. The AD570 is a selected version of the AD571 10-bit A-to-D converter.
Autor/Urheber: Dirkhb, Lizenz: CC BY-SA 3.0
Functional diagram of single-slope DAC
Autor/Urheber: Saure, Lizenz: CC BY-SA 3.0
Flash-Umsetzer mit 2 Bit, einschl. Kodeumsetzer
Autor/Urheber: Saure, Lizenz: CC BY-SA 3.0
Analog-Digital-Umsetzer mit rückgekoppeltem DAU (Serieller Umsetzer)
Autor/Urheber: Saure, Lizenz: CC BY-SA 3.0
Mehrstufiger ADU in Pipeline-Architektur
Zero-order hold signal
Autor/Urheber: Saure 10:29, 13. Apr. 2010 (CEST), Lizenz: CC BY-SA 3.0
Zeitlicher Verlauf bei der sukzessiven Approximation
Autor/Urheber: Mister rf, Lizenz: CC BY-SA 4.0
INTERSIL ICL7107. 31/2 Digit Single Chip A/D Converter The ICL7107 is a high performance, low power, 3.5 digit analog to digital converter. The IC includes internal circuitry for seven segment decoders, display drivers, reference voltage source and a clock.
Autor/Urheber: Mister rf, Lizenz: CC BY-SA 4.0
The ICL7107 is a high performance, low power, 3.5 digit analog to digital converter. The IC includes internal circuitry for seven segment decoders, display drivers, reference voltage source and a clock.