4D


4D oder 4-D ist eine verbreitete Abkürzung für vierdimensional als Angabe einer geometrischen Dimension.
4D ist eine Erweiterung der Darstellung von Körpern im 3D-Raum unserer Erfahrungswirklichkeit (Länge-Breite-Höhe, Koordinaten x,y,z) um eine unabhängige Hilfsdimension zur eindeutigen Erfassung der Position und Ausdehnung eines Körpers. Unter Verwendung von kartesischen Koordinaten x, y, z wird üblicherweise eine Achse mit der Bezeichnung w ergänzt.
Die vierte Dimension
Die Einführung mehrdimensionaler „Hyperräume“, die unserer direkten Erfahrung nicht zugänglich sind, ergibt sich aus den Bereichen der Höheren Mathematik bzw. der Physik. Zur Veranschaulichung von Räumen höherer Dimension wird z. B. der 3D-Raum um eine zusätzliche Dimension erweitert und die Körperdarstellung in den 3D-Raum projiziert.
In Verallgemeinerung der physikalischen Theorien Albert Einsteins wird die „vierte Dimension“ als durch die Zeit besetzt angenommen und der 4D-Raum mit dem Begriff Raumzeit gleichgesetzt. Verbindliche Annahmen der physikalischen Theorien bezüglich der Homogenität des Raumes (wonach alle Dimensionen hinsichtlich Qualität und Quantität ununterscheidbar sind) und der Betrachterinvarianz (wonach der Ursprung des Koordinatensystems und die Wahl der Achsen keinen Einfluss auf die Darstellung der Naturgesetze haben) legen jedoch nahe, dass die Zeit nicht als vierte Dimension angenommen werden kann. Ausprägungen von Raum können von denen der Zeit unterschieden werden, indem man z. B. versucht, einen Beobachter entlang einer Achse zu verschieben. Gelingt die Verschiebung, kann die Achse nicht die Zeit bedeuten.
Einsatzbereiche
Mathematisch-geometrisch anschauliche Herleitung
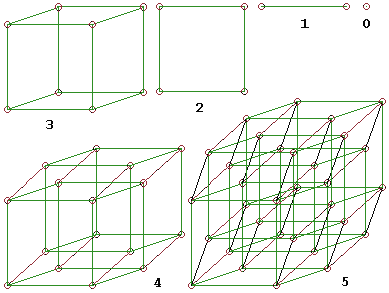
Eine (zusätzliche) Dimension bezeichnet eine Ausdehnung in eine Richtung, die nicht durch andere bereits vorher definierte Dimensionen dargestellt werden kann. Einerseits können Figuren in unserer Welt mehr oder weniger Dimensionen aufweisen, andererseits kann man sich eine Welt vorstellen, die mehr oder weniger Dimensionen hat. Als Beispiel möge der schrittweise Übergang vom Punkt (0D) zu 1D, 2D, 3D, 4D und 5D dienen:
- Dimension 0
Ein Punkt ohne Ausdehnung (ein Kreis mit Radius 0). Eine nulldimensionale Welt besteht nur aus einem einzigen Punkt.
- Dimension 1
In der Dimension 1 ist eine Bewegung in einer beliebigen Richtung vom Punkt weg möglich; man erhält eine Strecke. Beispielhaft ist die X-Achse eines Koordinatensystems, Ausdehnung nach links und rechts. In der eindimensionalen Welt existiert nur diese Linie, es existieren also auch nur zwei mögliche Richtungen. Hypothetische eindimensionale Feststoffe haben eine unveränderbare Reihenfolge und Orientierung, da sie nicht aneinander vorbei bewegt werden können.
- Dimension 2
Bei Dimension 2 suchen wir eine weitere Richtung, die nicht mit der ersten Strecke übereinstimmt, im einfachsten Fall: senkrecht auf die Strecke. Beispielsweise die Y-Achse eines Koordinatensystems, Ausdehnung nach vor und zurück. Dadurch erhalten wir ein Koordinatensystem, mit welchem wir jeden Punkt einer Ebene erreichen können. Hypothetische ein- und zweidimensionale Feststoffe haben keine feste Reihenfolge, da sie umeinander herum bewegt werden können. Nur zweidimensionale Objekte haben eine Orientierung, da eindimensionale Objekte um 180° gedreht werden können.
- Dimension 3
Für die Dimension 3 ist eine weitere Richtung nötig, die nicht in der Ebene (aus Dimension 2) liegt. Dazu zeigen wir einmal (vergleichbar dem Zeiger einer Uhr) in alle Richtungen der Ebene und schließen alle diese Richtungen aus. Zurück bleiben Richtungen, die nach oben oder unten zeigen. Im einfachsten Fall senkrecht auf der Ebene z. B. „nach oben“. Das ist die Z-Achse eines Koordinatensystems, Ausdehnung nach oben und unten. Dadurch erhalten wir ein Koordinatensystem, mit welchem wir jeden Punkt im Raum erreichen können. Nur dreidimensionale Objekte haben eine Orientierung: Eine rechte Hand kann nicht durch Drehungen und Bewegungen zu einer linken Hand werden, aber ein R kann gespiegelt werden und ist damit von einem Я nicht zu unterscheiden.
- Dimension 4
Wiederum ist eine Richtung erforderlich, die nicht im Raum (aus Dimension 3) liegt. Dazu zeigen wir kugelförmig in alle Richtungen, die wir uns vorstellen können, und schließen alle diese Richtungen aus. Zurück bleiben Richtungen, die wir uns mit unserem auf die Erfassung von drei Dimensionen ausgerichteten Verstand nicht (mehr) vorstellen können. Im einfachsten Fall steht diese senkrecht auf allen Richtungen, die wir uns vorstellen können. Erweitern wir den Raum in diese Richtung, haben wir einen 4-dimensionalen Hyperraum beschrieben. Hierfür wird die W-Achse eines Koordinatensystems eingeführt mit der Ausdehnung nach ana und kata, Begriffe geprägt von Charles Howard Hinton. Dreidimensionale Objekte haben keine Orientierung in 4D; eine rechte Hand kann durch die vierte Dimension so gedreht und wieder in der Hyperebene, aus der sie stammt, abgelegt werden, dass sie dort nun eine linke Hand ist.
Durch derart logische Überlegungen kann man errechnen, dass ein vierdimensionaler (Hyper-)Würfel (Tesserakt) 16 Ecken, 32 Kanten, 24 Flächen und 8 Volumina besitzt.
- Hyperwürfel
Jede Dimension kann man sich als Zusammensetzung einer unendlichen Anzahl der vorherigen Dimension entlang der neuen Dimensionsrichtung vorstellen. Die Gerade, mit der Dimension 1, ist so die Zusammenfügung einer unendlichen Anzahl Punkte der Dimension 0. Überträgt man diese Gedanken auf die „Vierte Dimension“, so ist diese die Zusammensetzung unendlich vieler (dreidimensionaler) Räume. Die Projektion eines vierdimensionalen Objekts entsteht im dreidimensionalen Raum als „Schatten“ stets in 3D. Dies darf nicht mit der Darstellung eines Schnitts des höherdimensionalen Objektes in der niedrigeren Dimension verwechselt werden.
Das Schattenmodell (meist als Gittermodell) entspricht einer Modellvorstellung des kompletten Objektes, während der Schnitt einem tatsächlichen Erscheinungsbild in der niedrigeren Dimension entspricht. Im Falle einer Bewegung des Objektes kann sich daher der Schnitt im Zeitverlauf ändern. Die zeitliche Entwicklung ist daher dafür geeignet, sich eine vierte Raumdimension vorzustellen. Dabei ändert sich nicht etwa das Objekt mit der Zeit, sondern nur sein Schnittbild.
Stellt man sich einen Tesserakt vor, der in Richtung der zusätzlichen Dimension unterschiedlich gefärbt ist, in diese ausgerichtet ist und sich nur in diese Richtung bewegt, so wird er zunächst in der niedrigdimensionalen Welt als Würfel sichtbar, ändert dann seine Farbe, bis er schließlich wieder verschwindet, ohne sich scheinbar zu bewegen. Die Bewegung entlang der höheren Dimension wird nur als Veränderung des Schnittbildes sichtbar und nicht als Koordinatenveränderung.
Physikalisch verbreitetes Verständnis
Gemäß der obigen mathematischen Definition ist ein vierdimensionales Koordinatensystem ein Koordinatensystem mit vier linear unabhängigen Richtungen. Dieses eignet sich, unsere bekannten drei Raumdimensionen und die Zeit-Dimension abzubilden.
In Einsteins Relativitätstheorie sind Raum und Zeit zu einer vierdimensionalen Raumzeit vereinigt. Der Raum zu einem bestimmten Zeitpunkt ist einfach eine Hyperfläche (in der Speziellen Relativitätstheorie eine Hyperebene) in der Raumzeit. Mathematisch ist die Projektion der Raumzeit auf einen gewöhnlichen dreidimensionalen Raum vergleichbar mit den Schnittebenen eines Würfels (Projektion von 3D nach 2D). Die „Richtung“ des Raumes (und der Zeit) in der Raumzeit ist nicht eindeutig bestimmt. In der Tat hängt die Wahl der Raum-Hyperebene vom Bezugssystem ab. Anschaulich darstellen lässt sich das in Minkowskidiagrammen, Näheres dazu findet sich auch unter Minkowskiraum.
Allerdings ist die Raumzeit – auch die ungekrümmte – nicht euklidisch, da ein Abstand zwischen zwei Punkten der flachen Raumzeit nicht durch die übliche Vektornorm definiert ist, sondern durch:
Aus dem negativen Quadrat folgt, dass die Abstände in der Zeit imaginäre Werte haben müssen.
Aus topologischen Gründen ist für die Einbettung eines gekrümmten 3D-Raumes keine vierte räumliche Dimension erforderlich.
Der 3D-Raum kann auch durch irgendeine andere Dimension als der Zeit als 4D-Raum oder Raum noch höherer Dimension verstanden werden. Dies lässt sich erreichen durch eine zusätzliche skalare Eigenschaft, wie bei 1D, oder eine Skala wie einer Farbskala. Dies kann z. B. bei Objekten auch die Materieeigenschaft der Temperatur, Masse oder Ladung oder die Raumeigenschaft des Gravitationspotentials etc. sein.
Kosmologische Bedeutung
Unsere erlernte Vorstellung erlaubt den dreidimensionalen Raum. Welche tatsächliche Ausdehnung der uns umgebende Raum in weiteren Richtungen hat, ist das Untersuchungsobjekt der Kosmologie.
4-dimensionale Körper
- Tesserakt, ein vierdimensionaler Hyperwürfel, verwandt mit dem dreidimensionalen Würfel
- Pentachoron, eine vierdimensionale Hyperpyramide, verwandt mit dem dreidimensionalen Tetraeder
- das vierdimensionale Hyperrechteck, verwandt mit dem dreidimensionalen Quader
- die vierdimensionale Hyperkugel (siehe auch Einheitskugel), verwandt mit der dreidimensionalen Kugel
- das vierdimensionale Kreuzpolytop, verwandt mit dem dreidimensionalen Oktaeder
4D-Flugführung
Technik, die Flugverkehr – in der Luft – nicht überwiegend nur räumlich ordnet, sondern zukünftig auch im Zeitablauf samt Fluggeschwindigkeit und Sinken koordiniert. Lotsen und Rechner wirken dann nicht mehr bloß als Separation-Manager, sondern als Verkehrsflussmanager, um dichteren Flugverkehr termingerechter und – etwa dank weniger Warteschleifen – energieeffizienter abzuwickeln. Anlässlich einer Testung im Februar 2012 wurde eine breite Einführung nicht vor 2018 in Aussicht gestellt.[1]
Weblinks
- http://www.4d-screen.de/related-space – Rotierende Körper im Hyperraum – z. B. 4d-plane, kleins bottle und hypercube
- http://www.dimensions-math.org/ Mehrsprachige Erklärungen und Videos zum Thema.
Einzelnachweise
- ↑ Reißverschlusssystem in der Luft. In: orf.at. 4. April 2012, abgerufen am 15. März 2024.
Auf dieser Seite verwendete Medien
Erstellt von Jason Hise mit Maya und Macromedia Fireworks. Eine 3D-Projektion eines 8-Zellers (Tesserakt), der eine einfache Rotation um eine Ebene ausführt. Letztere teilt die Figur von vorne links nach hinten rechts und von oben nach unten.
Autor/Urheber: Vitaly Ostrosablin, Lizenz: CC BY-SA 3.0
n-cubes from point to tesseract, created by movement of (n-1) cube over perpendicular axis.
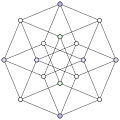
This pseudo-projection of the tesseract or 4-dimensional cube is very similar to the vertex-first-projection. This diagram shows the tesseract as the 4-dimensional measure-polytope, is thus a 4-dimensional cartesian coordinate-system in its 2-dimensional representation.
Autor/Urheber: de:Benutzer:Karl Bednarik, Lizenz: CC BY-SA 3.0
Parallelprojektionen der 0- bis 5-dimensionalen Würfelanaloga
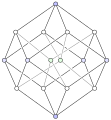
The 4D-hypercube, layered according to distance from one corner.
As described in "Alice in Wonderland" by the Cheshire Cat, this vertex-first-shadow of the tesseract forms a rhombic dodecahedron.
The two central vertices would coincide in an orthogonal projection from 4 to 3 dimensions, but here they were drawn slightly apart.
| This SVG was created with Inkscape. |