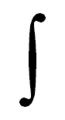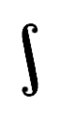Integralzeichen
∫ | |
|---|---|
| Mathematische Zeichen | |
| Arithmetik | |
| Pluszeichen | + |
| Minuszeichen | −, ⁒ |
| Malzeichen | ⋅, × |
| Geteiltzeichen | :, ÷, / |
| Plusminuszeichen | ±, ∓ |
| Vergleichszeichen | <, ≤, =, ≥, > |
| Wurzelzeichen | √ |
| Prozentzeichen | % |
| Analysis | |
| Summenzeichen | Σ |
| Produktzeichen | Π |
| Differenzzeichen, Nabla | ∆, ∇ |
| Prime | ′ |
| Partielles Differential | ∂ |
| Integralzeichen | ∫ |
| Verkettungszeichen | ∘ |
| Unendlichzeichen | ∞ |
| Geometrie | |
| Winkelzeichen | ∠, ∡, ∢, ∟ |
| Senkrecht, Parallel | ⊥, ∥ |
| Dreieck, Viereck | △, □ |
| Durchmesserzeichen | ⌀ |
| Mengenlehre | |
| Vereinigung, Schnitt | ∪, ∩ |
| Differenz, Komplement | ∖, ∁ |
| Elementzeichen | ∈ |
| Teilmenge, Obermenge | ⊂, ⊆, ⊇, ⊃ |
| Leere Menge | ∅ |
| Logik | |
| Folgepfeil | ⇒, ⇔, ⇐ |
| Allquantor | ∀ |
| Existenzquantor | ∃ |
| Konjunktion, Disjunktion | ∧, ∨ |
| Negationszeichen | ¬ |
Das Integralzeichen ist aus dem Buchstaben langes s („ſ“) als Abkürzung für das Wort Summe, lateinisch ſumma, entstanden. Diese symbolische Schreibweise von Integralen geht auf Gottfried Wilhelm Leibniz zurück. Für das Integralzeichen gibt es eine Reihe von Abwandlungen, unter anderem für Mehrfachintegrale, Kurvenintegrale, Oberflächenintegrale und Volumenintegrale.
Geschichte
Leibniz erwähnte in einem später veröffentlichten Manuskript Analysis tetragonistica vom 29. Oktober 1675 erstmals das Integralzeichen.[1]
„Utile erit scripsisse ∫ pro omnia“
„Es wird nützlich sein, ∫ für omnia zu schreiben“
Omnia steht dabei für omnia l und wird in dem geometrisch orientierten Flächenberechnungsverfahren von Bonaventura Cavalieri verwendet. Die zugehörige gedruckte Veröffentlichung Leibniz’ ist De geometria recondita et analysi indivisibilium et infinitorum (lat. für „Über eine verborgene Geometrie und die Analyse des Unteilbaren und des Unendlichen“), aus dem Jahr 1686. Damals nannte er die Integralrechnung noch calculus summatorius, deshalb das lange S. Auch Johann I Bernoulli beschäftigte sich zu der Zeit mit dem Thema, und da Leibniz einheitliche wissenschaftliche Zeichen anstrebte, diskutierten sie darüber. So blieb das Zeichen von Leibniz und der Name calculus integralis, Integralrechnung, von Bernoulli.[2]
Verwendung
Das Integral einer reellen Funktion bezüglich der Variablen über das Intervall wird durch
notiert. Die multiplikativ zu lesende Notation deutet dabei an, wie sich die Integraloperation aus Streifen der Höhe und der infinitesimalen Breite zur Fläche unter der Funktion summiert.
Traditionen des Formelsatzes
In den verschiedenen Traditionen des Formelsatzes haben sich leicht unterschiedliche Formen des Integralzeichens eingebürgert. So wird im deutschen Formelsatz die im Bild Deutsche Form des Integralzeichens abgebildete Form verwendet, während beispielsweise im russischen Raum sich eine Formvariante etabliert hat, die die Graphik Russische Formvariante des Integralzeichens wiedergibt.[3]
Deutsche Form des Integralzeichens
Russische Formvariante des Integralzeichens
Außerdem werden im amerikanischen Satz in Textformeln die oberen und unteren Grenzen rechts des Integralzeichens angeordnet, um störende Zeilenabstände einzuschränken,
während in deutscher Tradition
üblich ist. Auch sind Integrale in Textformeln immer kleiner als in abgesetzten Formeln.
Kodierung
Das Integralzeichen und seine Abwandlungen werden in Computersystemen folgendermaßen kodiert.
| Zeichen | Unicode | Bezeichnung | HTML | LaTeX[4] | |||
|---|---|---|---|---|---|---|---|
| Position | Bezeichnung | hexadezimal | dezimal | benannt | |||
| ∫ | U+222B | integral | Integral | ∫ | ∫ | ∫ | \int |
| ∬ | U+222C | double integral | Doppelintegral | ∬ | ∬ | \iint | |
| ∭ | U+222D | triple integral | Dreifachintegral | ∭ | ∭ | \iiint | |
| ∮ | U+222E | contour integral | Kurvenintegral | ∮ | ∮ | \oint | |
| ∯ | U+222F | surface integral | Oberflächenintegral | ∯ | ∯ | \oiint | |
| ∰ | U+2230 | volume integral | Volumenintegral | ∰ | ∰ | \oiiint | |
| ∱ | U+2231 | clockwise integral | rechtsläufiges Integral | ∱ | ∱ | \intclockwise | |
| ∲ | U+2232 | clockwise contour integral | rechtsläufiges Kurvenintegral | ∲ | ∲ | \ointclockwise | |
| ∳ | U+2233 | anticlockwise contour integral | linksläufiges Kurvenintegral | ∳ | ∳ | \ointctrclockwise | |
| ⌠ | U+2320 | top half integral | obere Hälfte eines Integrals | ⌠ | ⌠ | ||
| ⌡ | U+2321 | bottom half integral | untere Hälfte eines Integrals | ⌡ | ⌡ | ||
| ⎮ | U+23AE | integral extension | Erweiterung eines Integrals | ⎮ | ⎮ | ||
| ⨋ | U+2A0B | summation with integral | Integralsumme | ⨋ | ⨋ | \sumint | |
| ⨌ | U+2A0C | quadruple integral operator | Vierfachintegral | ⨌ | ⨌ | \iiiint | |
| ⨍ | U+2A0D | finite part integral | Integral mit endlichem Teil | ⨍ | ⨍ | \dashint | |
| ⨎ | U+2A0E | integral with double stroke | Integral mit Doppelstrich | ⨎ | ⨎ | \ddashint | |
| ⨏ | U+2A0F | integral average with slash | Mittelwertintegral mit Querstrich | ⨏ | ⨏ | \strokedint | |
| ⨑ | U+2A11 | anticlockwise integration | linksläufiges Integral | ⨑ | ⨑ | \intctrclockwise | |
| ⨕ | U+2A15 | integral around a point operator | Integral um einen Punkt | ⨕ | ⨕ | ||
| ⨖ | U+2A16 | quaternion integral operator | Quaternionenintegral | ⨖ | ⨖ | \sqint | |
| ⨗ | U+2A17 | integral with leftwards arrow with hook | Integral mit Linkspfeil mit Haken | ⨗ | ⨗ | ||
| ⨘ | U+2A18 | integral with times sign | Integral mit Malzeichen | ⨘ | ⨘ | ||
| ⨙ | U+2A19 | integral with intersection | Integral mit Durchschnitt | ⨙ | ⨙ | \landdownint | |
| ⨚ | U+2A1A | integral with union | Integral mit Vereinigung | ⨚ | ⨚ | \landupint | |
| ⨛ | U+2A1B | integral with overbar | Integral mit Überstrich | ⨛ | ⨛ | ||
| ⨜ | U+2A1C | integral with underbar | Integral mit Unterstrich | ⨜ | ⨜ | ||
Weblinks
Einzelnachweise
- ↑ Carl von Prantl: Leibniz, Gottfried Wilhelm. In: Allgemeine Deutsche Biographie (ADB). Band 18, Duncker & Humblot, Leipzig 1883, S. 172–209., suche calculus summatorius
- ↑ Alfred Warner, Historisches Wörterbuch der Elektrotechnik, Informationstechnik und Elektrophysik
- ↑ Zaitcev, V.; Janishewsky, A.; Berdnikov, A. (1999), Russian Typographical Traditions in Mathematical Literature. EuroTeX'99 Proceedings (Online (Memento vom 28. September 2012 im Internet Archive); PDF; 200 kB)
- ↑ Scott Pakin: The Comprehensive LaTeX Symbol List. (PDF; 21 MB) 5. Mai 2021, archiviert vom am 18. Juli 2021; abgerufen am 19. Juli 2021 (englisch, der Originallink führt zu einem Spiegelserver des CTAN; zum Archivlink vergleiche Datei:Comprehensive LaTeX Symbol List.pdf).
Auf dieser Seite verwendete Medien
Russische Formvariante des Integralzeichens
Deutsche Form des Integralsymbols