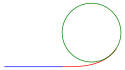
Übergangsbogen

Der Übergangsbogen ist ein Trassierungselement, das beim Bau von Verkehrswegen als Verbindung zwischen einer Geraden und einem Kreisbogen oder zwischen zwei Kreisbögen verwendet wird. Er zeichnet sich dadurch aus, dass er wie eine Ellipse und im Gegensatz zu Gerade und Kreisbogen an jeder Stelle einen anderen Krümmungsradius aufweist.

Dies bewirkt, dass beim Übergang zwischen Gerade und Kreisbogen die Kurve nur allmählich (${\displaystyle G^{2}}$-stetig) und nicht sprungartig enger wird.

Auf einer Straße ohne Übergangsbogen müsste das Lenkrad beim Übergang von der geraden Fahrbahn in eine Kurve ruckartig eingeschlagen werden. Mit Übergangsbogen kann dagegen langsam von der Mittelposition bis zum notwendigen Einschlag des Lenkrads gelenkt werden.

Zweck eines Übergangsbogens ist es, die in der Kurve auftretenden Fliehkräfte beim Durchfahren kontinuierlich auf- bzw. abzubauen und nicht plötzlich. Ohne Übergangsbogen würden auch bei der Einfahrt in den Looping einer Achterbahn zu hohe Beschleunigungskräfte auf Passagiere und Konstruktion einwirken.

Mit gleichem Radius aneinanderstoßende Übergangsbögen werden Scheitelbogen genannt. Übergangsbögen, die Kreisbögen verschiedener Radien verbinden, werden als Eilinie bezeichnet.

Die am häufigsten verwendeten Übergangsbögen sind die Klothoide, die Sinusoide und die kubische Parabel. Bei der Deutschen Bahn werden auch ein s-förmiger Übergangsbogen (Übergangsbogen nach Schramm, Parabel vierter Ordnung) und der Blossbogen (Parabel fünfter Ordnung) verwendet. Da der Übergangsbogen nach Bloss günstigere fahrdynamische Eigenschaften sowie eine kürzere Entwicklungslänge aufweist, wird der s-förmige Übergangsbogen bei Um- und Neubauten nicht mehr verwendet.

Eine neue Entwicklung ist der Wiener Bogen, bei dem auch der Schwerpunkt eines Fahrzeugs berücksichtigt wird.

Das Abrückmaß ${\displaystyle f}$ (auch Tangentenabrückung genannt) ist der Abstand der Geraden vom Kreis. Es hängt von der gewählten Kurvenform ab – zwei Beispiele:

${\displaystyle f\approx {\frac {l_{\mathrm {u} }^{2}}{24\cdot r}}}$ (kubische Parabel)

${\displaystyle f\approx {\frac {l_{\mathrm {u} }^{2}}{48\cdot r}}}$ (Parabel 4. Grades)

Darin sind ${\displaystyle l_{\mathrm {u} }}$ die Länge des Übergangsbogens und ${\displaystyle r}$ der Radius des Kreisbogens.

Als Formelzeichen für die Länge von Übergangsbögen werden in Lageplänen in Deutschland ${\displaystyle l_{U}}$ (Klothoide), ${\displaystyle l_{US}}$ (s-förmig) bzw. ${\displaystyle l_{UB}}$ (nach Bloss) verwendet.

Durch die auch mit ETCS mögliche meter- und 5-km/h-genaue Geschwindigkeitssignalisierung können Geschwindigkeitswechsel auch in Übergangsbögen angeordnet werden, um früher beschleunigen zu können bzw. später bremsen zu müssen.^[1]

Geschichte

Im frühen 20. Jahrhundert wurden Übergangsbögen entworfen, um im Nachtzug- und Speisewagen-Betrieb einen besseren Fahrkomfort zu erreichen. Bei Gleiserneuerungen wurden Ende der 1920er Jahre an Bogenanfängen und -enden grundsätzlich Übergangsbögen in Form kubischer Parabeln angeordnet, die auf Strecken mit Höchstgeschwindigkeiten über 80 km/h mit dem 1000-fachen Verzug der Gleisüberhöhung errechnet wurden und länger als vorherige Übergangsbögen waren.^[2] In Vorgängerregelungen (BO, TV) war in den 1920er Jahren vorgesehen, einen Übergangsbogen von mindestens der 300-fachen Länge der Überhöhung bei höchstzulässiger Geschwindigkeit anzuordnen. In Preußen sollte aus Komfortgründen möglichst das 600-Fache nicht unterschritten werden.^[3]

Nachdem ausreichend Erfahrungen mit der Ausbildung und Anordnung von Übergangsbögen vorlagen, wurde in die Eisenbahn-Bau- und Betriebsordnung vom 8. Mai 1967 die allgemeine Forderung aufgenommen, wo erforderlich Übergangsbögen anzuordnen. Zuvor waren Bestimmungen zu Übergangsbögen durch die Aufsichtsbehörde erlassen worden.^[4]

Einzelnachweise

1. ↑ Thomas Berner, Christian Frye, Lena Henzler, Peter Reinhart, David Schäfer, Fabian Walf: Der Pfaffensteigtunnel nimmt Kontur an. In: Der Eisenbahningenieur. Band 73, Nr. 11, November 2022, ISSN 0013-2810, S. 47–52 (PDF). 
2. ↑ Müller: Der Oberbau der Reichsbahn in der Nachkriegszeit. In: Die Reichsbahn. Band 6, Nr. 38 / 39, 17. September 1930, ZDB-ID 512289-2, S. 1005–1013 / 1029–1039. 
3. ↑ Erich Giese, Otto Blum, Kurt Risch: Linienführung (= Robert Otzen [Hrsg.]: Handbibliothek für Bauingenieure. Band 2, Nr. 2). Julius Springer, Berlin 1925, S. 213 f. 
4. ↑ Heinz Delvendahl: Die Bahnanlagen in der neuen Eisenbahn-Bau- und Betriebsordnung (EBO). In: Die Bundesbahn. Band 41, Nr. 13/14, 1967, ISSN 0007-5876, S. 453–460.